X
Код презентации скопируйте его
Арифметические действия в двоичной системе счисления
Скачать эту презентацию
Презентация на тему Арифметические действия в двоичной системе счисления
Скачать эту презентациюCлайд 1
Cлайд 2
ЗАДАНИЕ «ТЕЗИСЫ» Верно ли каждое из следующих утверждений? Если «Да», то записывайте 1. Если «Нет», то записывайте 0. В результате должно получиться двоичное число.
Cлайд 3
Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. ТЕЗИСЫ 1 или 0 ? ? Все системы счисления делятся на три большие группы: позиционные, непозиционные и полупозиционные. В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Основанием двоичной системы счисления является число 4 Число А21СFD4 записано в шестнадцатиричной системе счисления. Число 1567 записано с ошибкой. Число 10, записанное в десятичной системе счисления, в двоичной системе счисления записывается как 1011 Число 10, записанное в десятичной системе счисления, меньше числа 10, записанного в восьмеричной системе счисления. Число 3005,234 записано с ошибкой. Число 6398 записано в восьмеричной системе счисления.
Cлайд 4
Полученное двоичное число переведите в десятичную, восьмеричную и шестнадцатиричную системы счисления.
Cлайд 5
Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. ТЕЗИСЫ 1 Все системы счисления делятся на три большие группы: позиционные, непозиционные и полупозиционные. В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Основанием двоичной системы счисления является число 4 Число А21СFD4 записано в шестнадцатиричной системе счисления. Число 1567 записано с ошибкой. Число 10, записанное в десятичной системе счисления, в двоичной системе счисления записывается как 1011 Число 10, записанное в десятичной системе счисления, меньше числа 10, записанного в восьмеричной системе счисления. Число 3005,234 записано с ошибкой. Число 6398 записано в восьмеричной системе счисления. 0 1 0 1 0 0 0 1 0
Cлайд 6
10101000102 = 67410 10101000102 = 12428 10101000102 = 2А216
Cлайд 7
Пьер Симон Лаплас французский астроном, математик и физик (1749 – 1827 гг.) «Мысль – выражать все числа немногими знаками, придавая им значение по форме, её значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна …» Пьер Симон Лаплас о своем отношении к двоичной (бинарной) системе счисления Эти слова подчеркивают универсальность алфавита, состоящего из двух символов. «В своей бинарной арифметике Лейбниц видел прообраз творения. Ему представлялось, что единица представляет божественное начало, а нуль – небытие и что высшее существо создает все из небытия точно таким же образом, как единица и нуль в его системе выражают все числа…».
Cлайд 8
Все позиционные системы счисления «одинаковы», а именно, во всех них выполняются арифметические операции по одним и тем же правилам: справедливы одни и те же законы арифметики: -коммутативный (переместительный) m + n = n + m m · n = n · m ассоциативный (сочетательный) ( m + n ) + k = m + ( n + k ) = m + n + k (m · n ) · k = m · ( n · k ) = m · n · k дистрибутивный (распределительный) ( m + n ) · k = m · k + n · k справедливы правила сложения, вычитания, умножения и деления столбиком; правила выполнения арифметических операций опираются на таблицы сложения и умножения.
Cлайд 9
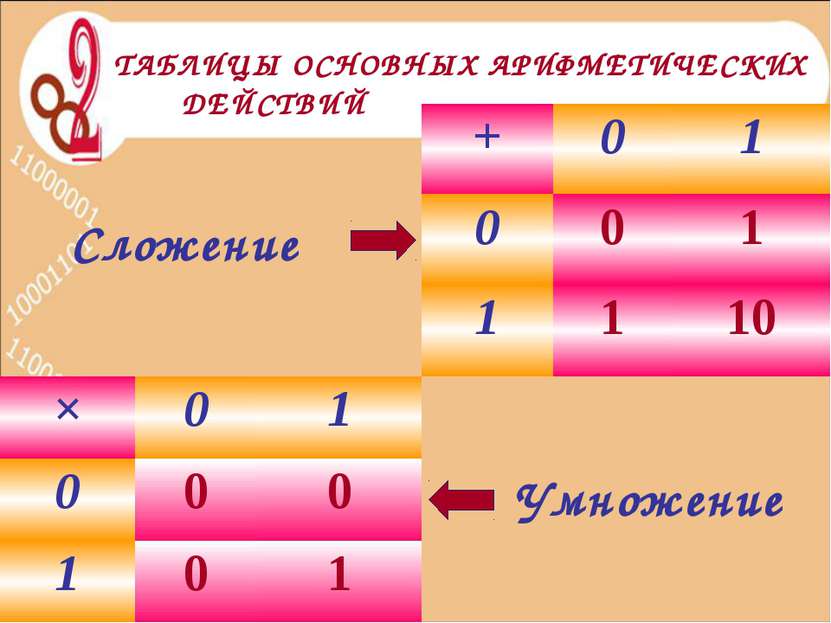
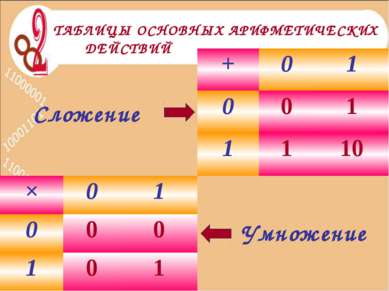Сложение Умножение ТАБЛИЦЫ ОСНОВНЫХ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ + 0 1 0 0 1 1 1 10 × 0 1 0 0 0 1 0 1
Cлайд 10
ДОМАШНЕЕ ЗАДАНИЕ 1) Выучить правила выполнения арифметических действий в двоичной системе счисления, выучить таблицы сложения, вычитания, умножения. 2) Выполнить задания: Заданы двоичные числа X и Y. Вычислите X+Y и X–Y, если: а) X=1000111, Y=11010 б) X=100111, Y=1101 Заданы двоичные числа X и Y. Вычислите X+Y–1001101, если: а) X=1010100, Y=110101 б) X=100111, Y=1101 Заданы двоичные числа X и Y. Вычислите X*Y и X:Y, если: а) X=11001, Y=101 б) X=100111, Y=1101
Cлайд 11
: - ) - радостное лицо : - ( - грустное лицо ; - ) - подмигивающая улыбка : 0 ) - клоун 8:-) - маленькая девочка
Cлайд 12
