X
Код презентации скопируйте его
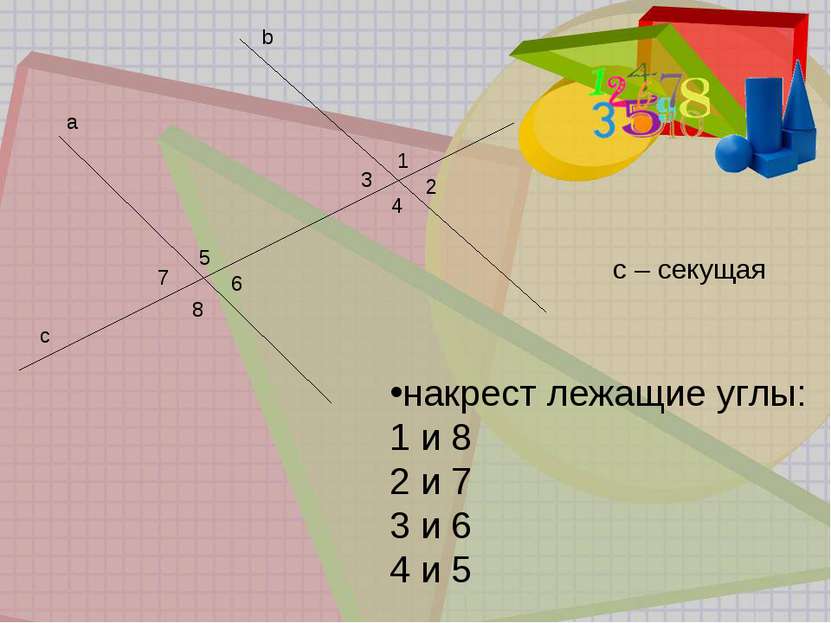
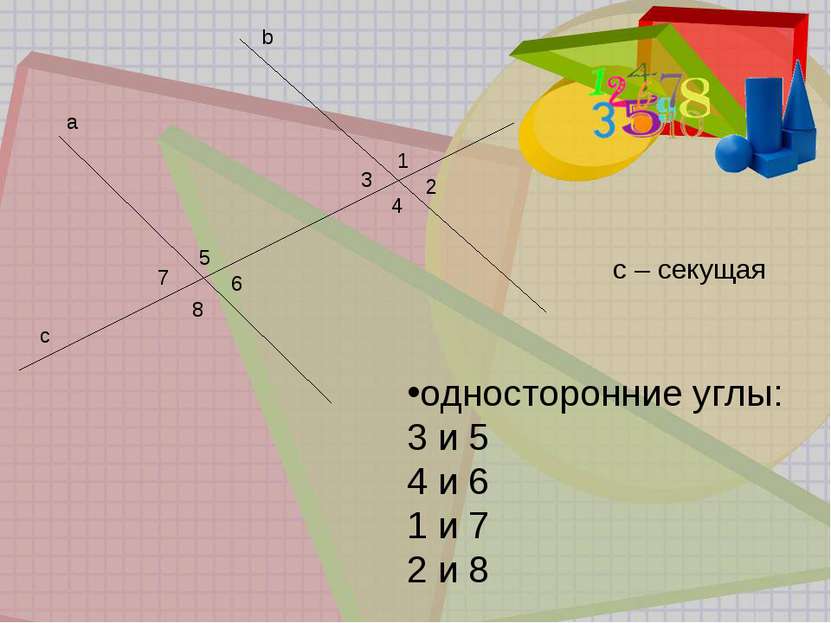
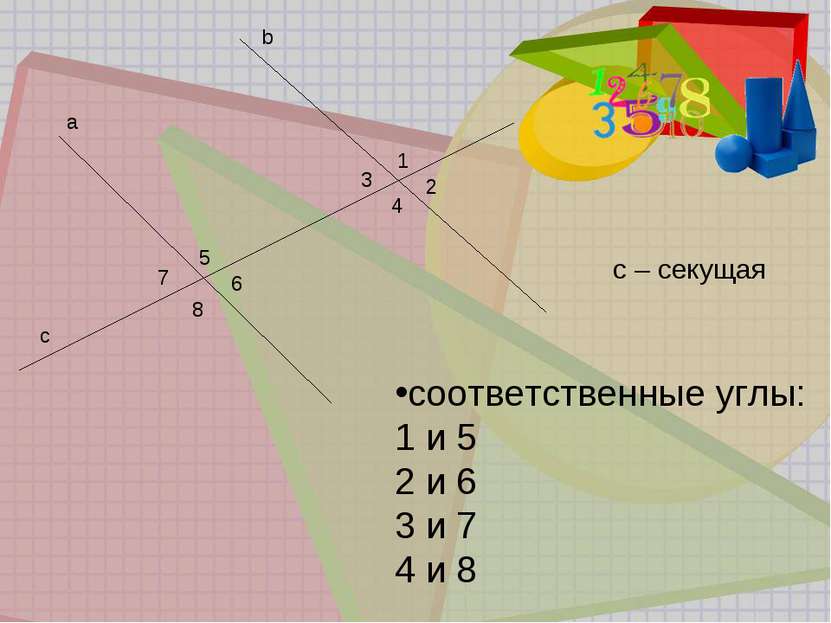
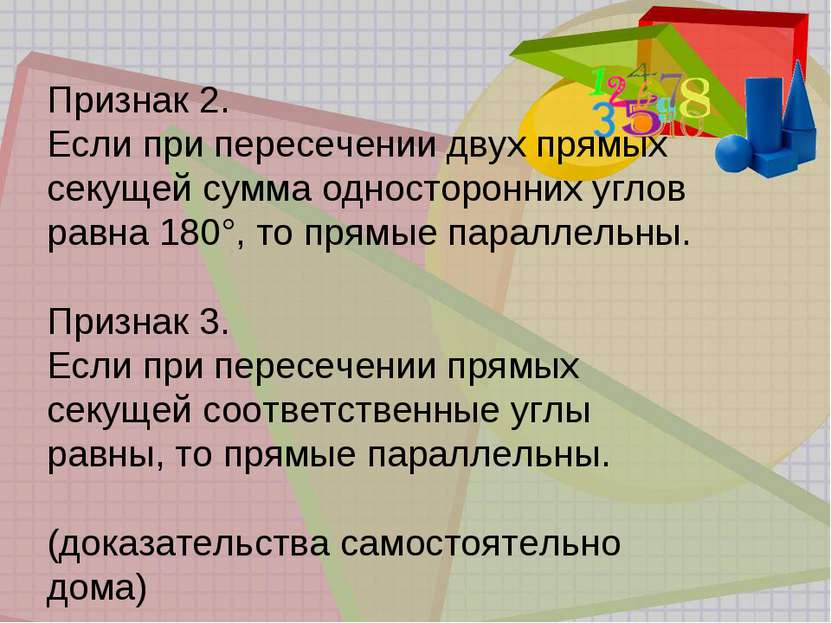
Признаки параллельных прямых
Скачать эту презентацию
Презентация на тему Признаки параллельных прямых
Скачать эту презентациюCлайд 1
«Признаки параллельных прямых» Подготовила учитель математики МБОУ гимназии №1 Левшина Мария Александровна
Cлайд 2
Цели: Закрепить знания учащимися видов углов, образованных в результате пересечения двух прямых секущей; изучить признаки параллельности прямых; формирование умений анализировать изученный материал и навыков применения его для решения задач; показать значимость изучаемых понятий; закрепить навыков решения задач на применение признаков параллельности прямых; развитие познавательной активности и самостоятельности получения знаний; воспитание интереса к предмету, самостоятельности.
Cлайд 3
Две прямые параллельны, если они не пересекаются. а b
Cлайд 4
b a 1 2 3 4 5 6 7 8 c с – секущая накрест лежащие углы: 1 и 8 2 и 7 3 и 6 4 и 5
Cлайд 5
b a 1 2 3 4 5 6 7 8 c с – секущая односторонние углы: 3 и 5 4 и 6 1 и 7 2 и 8
Cлайд 6
b a 1 2 3 4 5 6 7 8 c с – секущая соответственные углы: 1 и 5 2 и 6 3 и 7 4 и 8
Cлайд 7
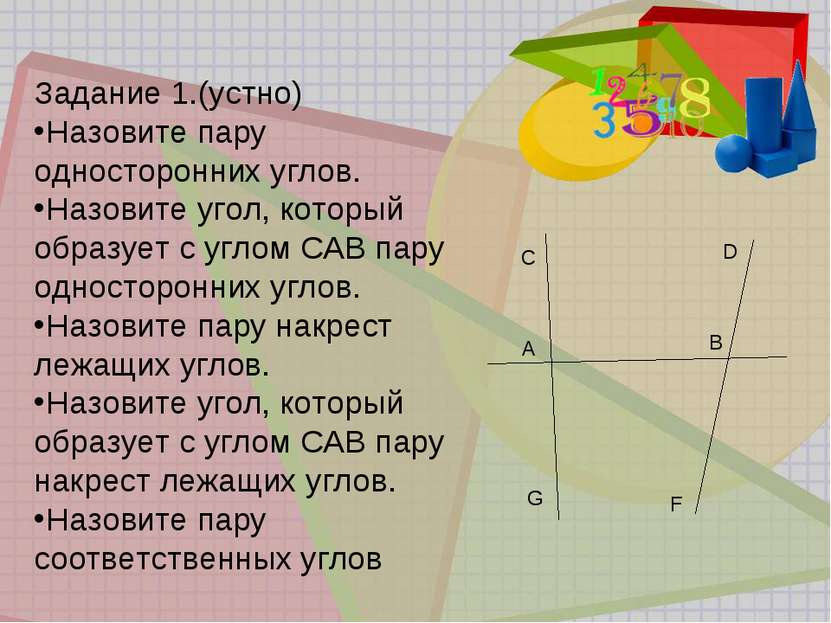
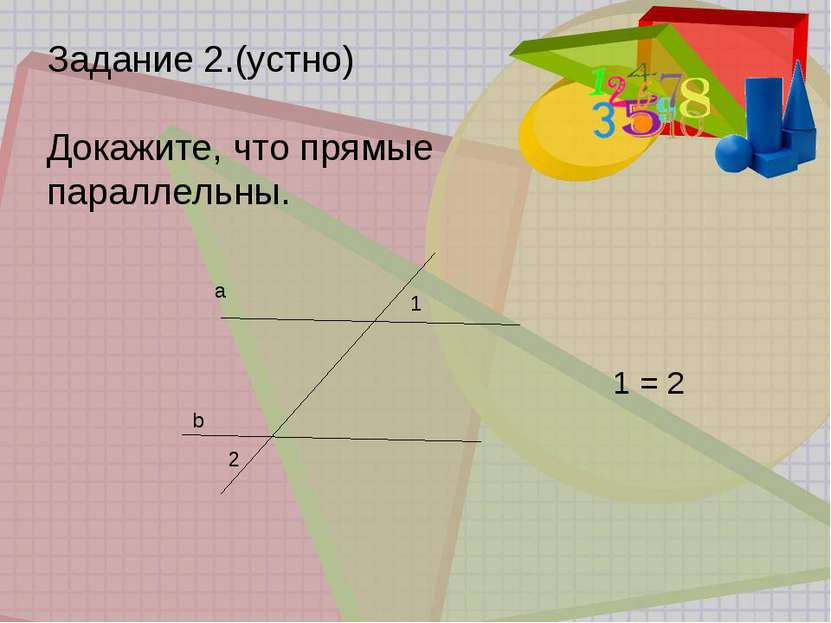
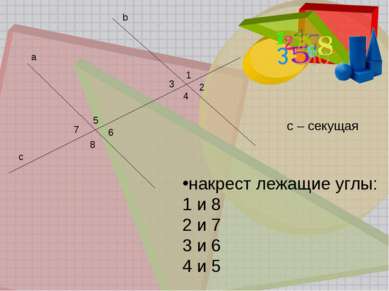
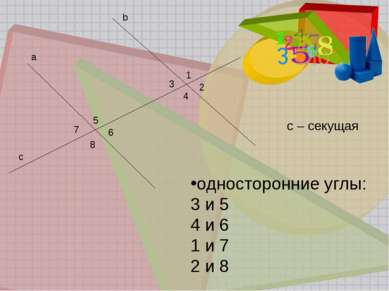
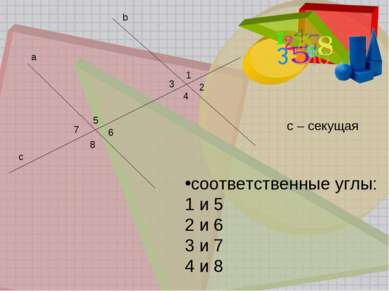
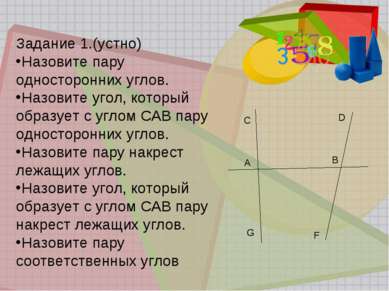Задание 1.(устно) Назовите пару односторонних углов. Назовите угол, который образует с углом САВ пару односторонних углов. Назовите пару накрест лежащих углов. Назовите угол, который образует с углом САВ пару накрест лежащих углов. Назовите пару соответственных углов C A G D B F
Cлайд 8
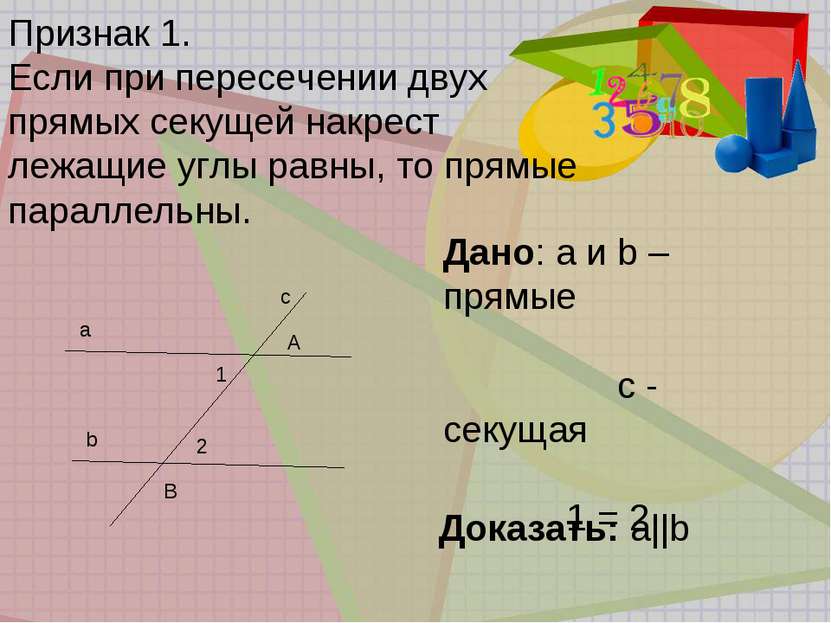
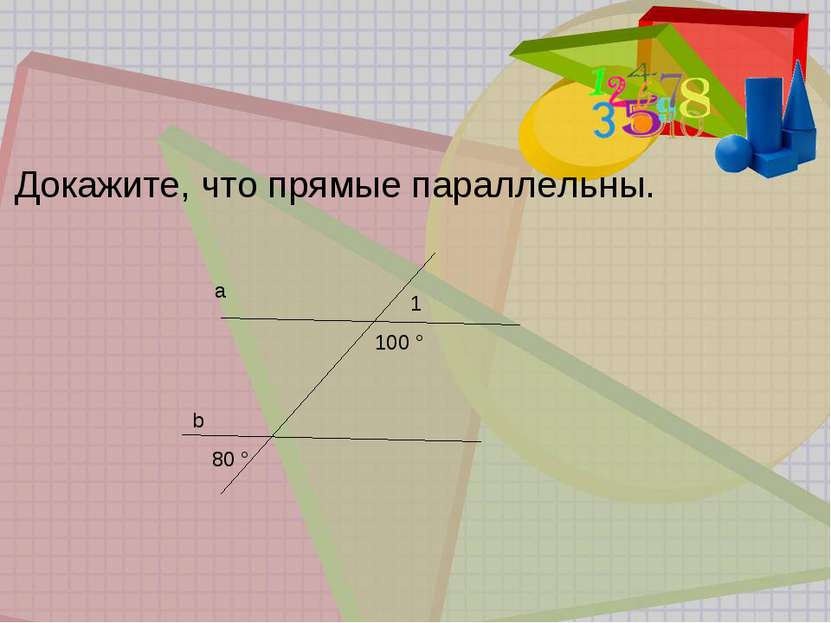
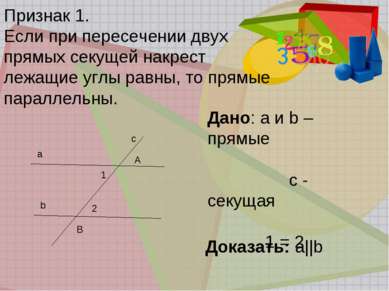Признак 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. Дано: а и b – прямые с - секущая 1 = 2 Доказать: а||b a b c A B 1 2
Cлайд 9
Доказательство : Случай 1. Угол 1 и 2 по 90°.По теореме о двух прямых, перпендикулярных третьей, а ||‖ b а b c A B 1 2
Cлайд 10
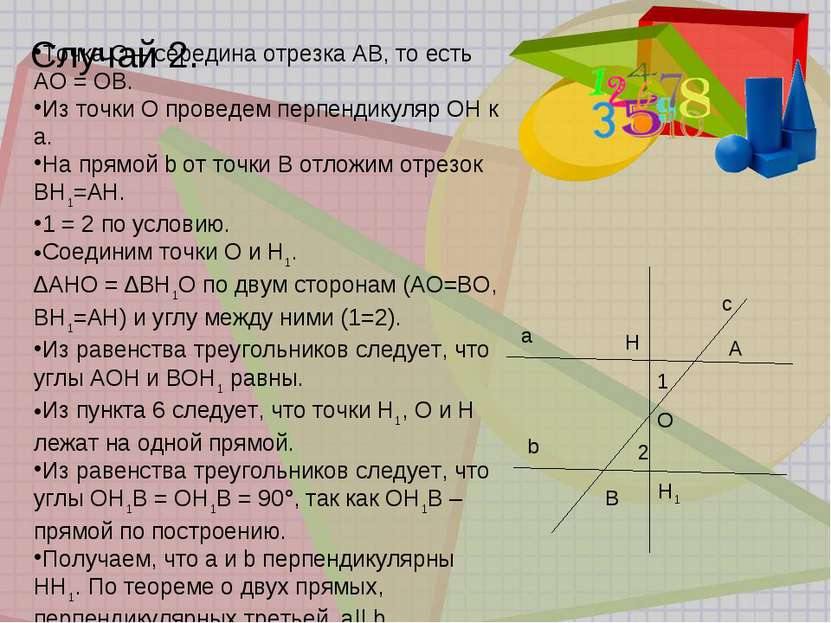
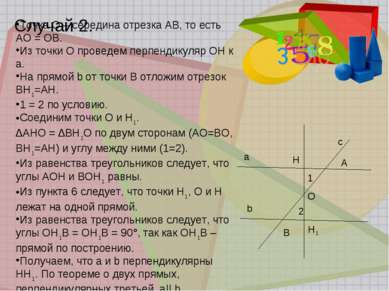Случай 2. a b c A B 1 2 H H1 O Точка О – середина отрезка АВ, то есть АО = ОВ. Из точки О проведем перпендикуляр ОН к а. На прямой b от точки В отложим отрезок ВН1=АН. 1 = 2 по условию. Соединим точки О и Н1. ∆АНО = ∆ВН1О по двум сторонам (АО=ВО, ВН1=АН) и углу между ними (1=2). Из равенства треугольников следует, что углы АОН и ВОН1 равны. Из пункта 6 следует, что точки Н1, О и Н лежат на одной прямой. Из равенства треугольников следует, что углы ОН1В = ОН1В = 90°, так как ОН1В – прямой по построению. Получаем, что а и b перпендикулярны НН1. По теореме о двух прямых, перпендикулярных третьей, а|| b.
Cлайд 11
Признак 2. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны. Признак 3. Если при пересечении прямых секущей соответственные углы равны, то прямые параллельны. (доказательства самостоятельно дома)
Cлайд 12
Задание 2.(устно) Докажите, что прямые параллельны. 1 = 2 a b 2 1
Cлайд 13
a b 80 ° 1 100 ° Докажите, что прямые параллельны.
Cлайд 14
№187, № 192 Домашнее задание. §1, вопросы 1-6.№188, №193
