X
Код презентации скопируйте его
Признаки параллельности прямых. Свойства параллельных прямых
Скачать эту презентацию
Презентация на тему Признаки параллельности прямых. Свойства параллельных прямых
Скачать эту презентациюCлайд 1
Признаки параллельности прямых. Свойства параллельных прямых.
Cлайд 2
Cлайд 3
УСТАНОВИТЕ СООТВЕТСТВИЕ: 2 и 3 накрест лежащие 7 и 4 5 и 7 соответственные 5 и 4 3 и 4 односторонние 4 и 8 1 и 4 вертикальные 1 и 3 7 и 3 смежные 8 и 7 6 и 8 2 и 5
Cлайд 4
Экспресс – опрос. 2 вариант. 1 вариант. Будет ли a ׀׀ b (рис. 1), если 6 = 3 3 = 134°; 2 = 56° 5 = 4 5 = 61°; 8 = 129° Если a ׀׀ b (рис. 2), то верно ли, что 6 + 4 = 180° 2 = 7 5 + 3 = 180° 1 = 8 6 2 1 5 8 4 3 7 1 2 3 4 5 6 7 8 a b c a b c рис.1 рис.2
Cлайд 5
Домашнее исследование. Пируев Дмитрий Софонова Екатерина Лаптев Борис
Cлайд 6
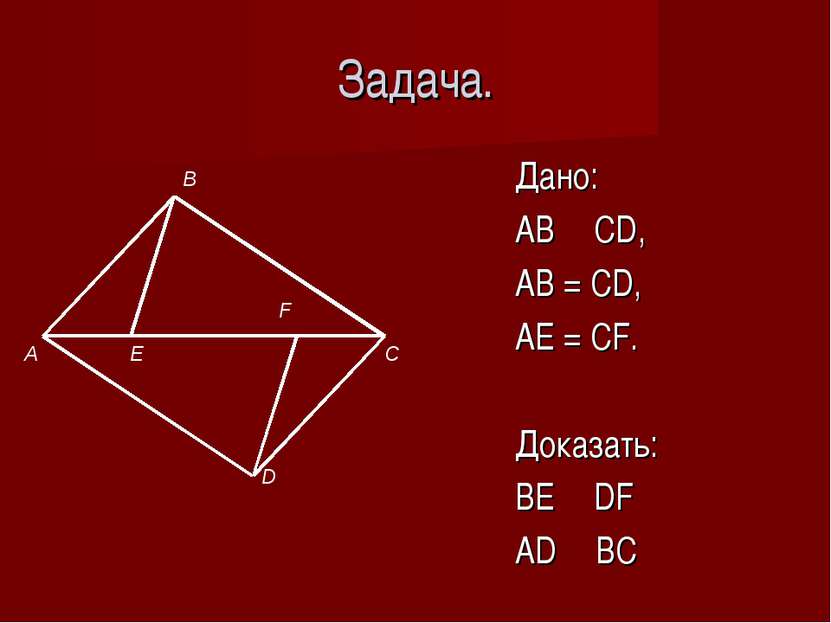
Решение задач по теме: «Признаки параллельности прямых. Свойства параллельных прямых.» Подготовил: ученик 7б класса МОУ СОШ №10 г. Павлово Пируев Дмитрий
Cлайд 7
Задача. Дано: АВ ׀׀ CD, AB = CD, AE = CF. Доказать: BE׀׀ DF AD ׀׀ BC
Cлайд 8
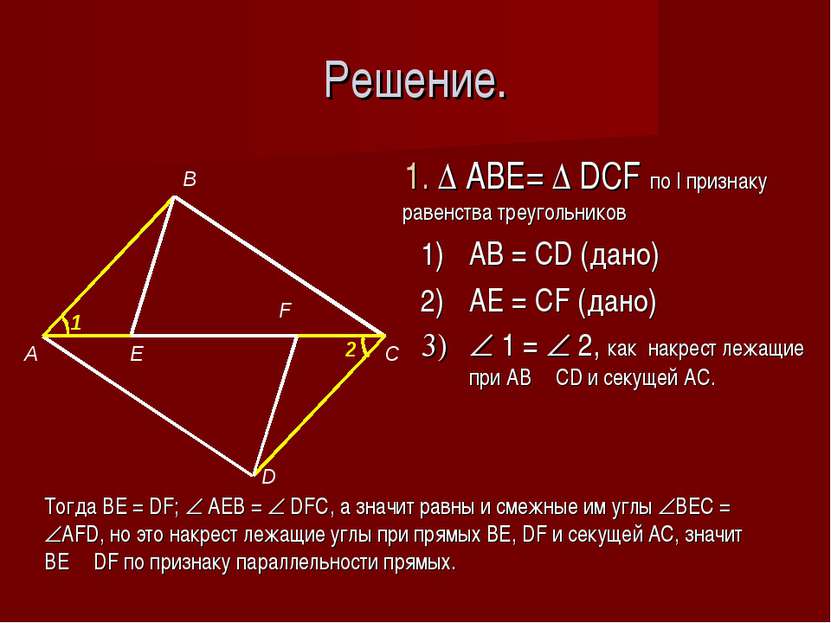
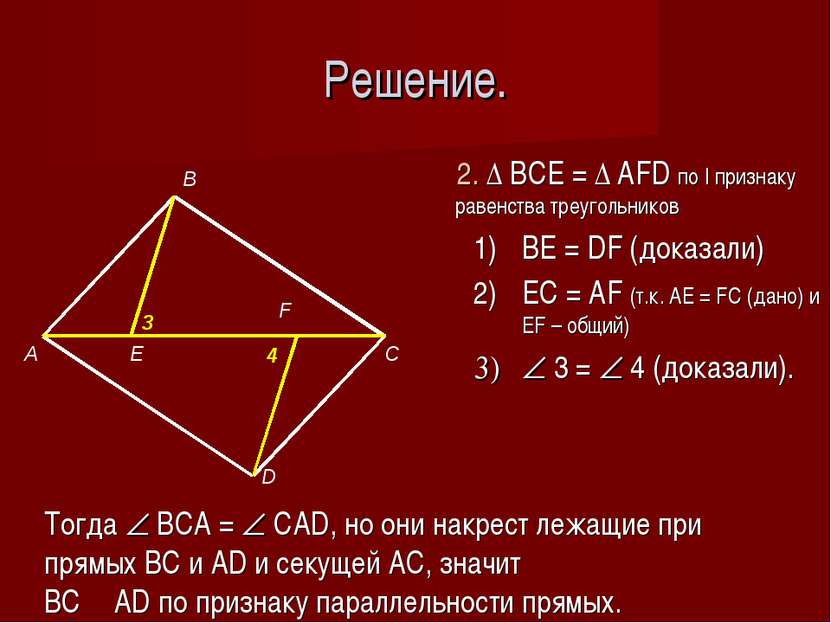
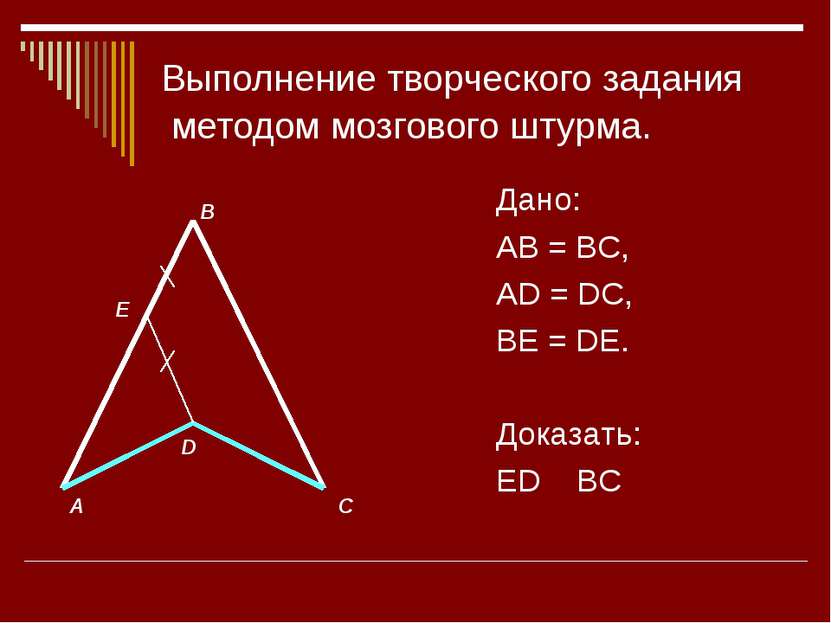
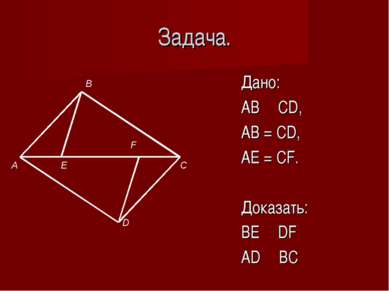
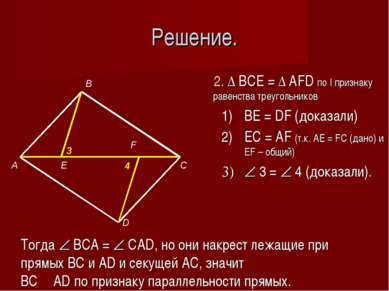
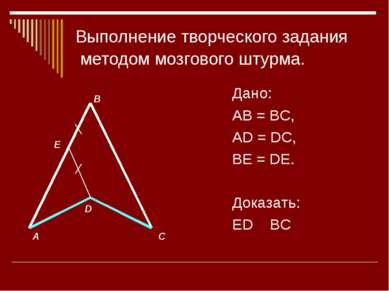
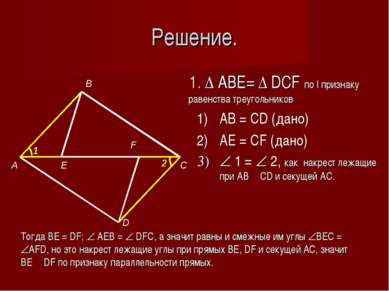Решение. 1. Δ ABE= Δ DCF по I признаку равенства треугольников AB = CD (дано) AE = CF (дано) 1 = 2, как накрест лежащие при AB ׀׀ CD и секущей AC. 1 2 Тогда BE = DF; AEB = DFC, а значит равны и смежные им углы BEC = AFD, но это накрест лежащие углы при прямых ВЕ, DF и секущей АС, значит ВЕ ׀׀ DF по признаку параллельности прямых.
Cлайд 9
Решение. 2. Δ BCE = Δ AFD по I признаку равенства треугольников BE = DF (доказали) EC = AF (т.к. AE = FC (дано) и ЕF – общий) 3 = 4 (доказали). 3 4 Тогда BCA = CAD, но они накрест лежащие при прямых BC и AD и секущей AC, значит BC ׀׀ AD по признаку параллельности прямых.
Cлайд 10
Групповая работа.
Cлайд 11
Выполнение творческого задания методом мозгового штурма. Дано: AB = BC, AD = DC, BE = DE. Доказать: ED ׀׀ BC A B C D E
