X
Код презентации скопируйте его
График производной функции. График функции
Скачать эту презентацию
Презентация на тему График производной функции. График функции
Скачать эту презентациюCлайд 1
ГРАФИК ПРОИЗВОДНОЙ ФУНКЦИИ, ГРАФИК ФУНКЦИИ Учитель математики Кидалова Лариса Леонидовна, МАОУ №47, г.Иркутск, 2015г. Подготовка к ЕГЭ
Cлайд 2
Cлайд 3
Cлайд 4
Ответ: 1
Cлайд 5
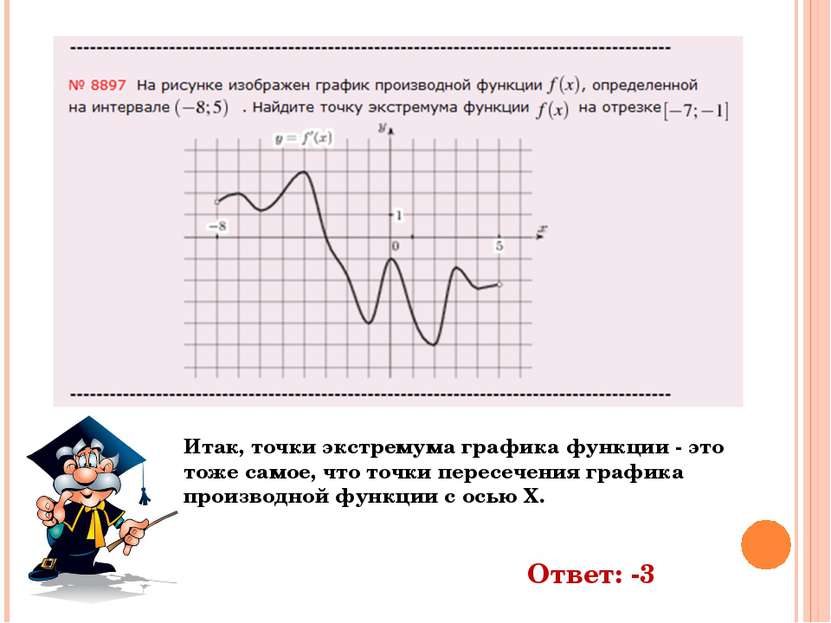
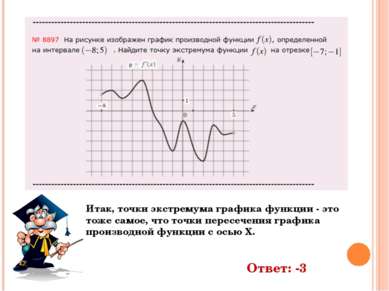Итак, точки экстремума графика функции - это тоже самое, что точки пересечения графика производной функции с осью Х. Ответ: -3
Cлайд 6
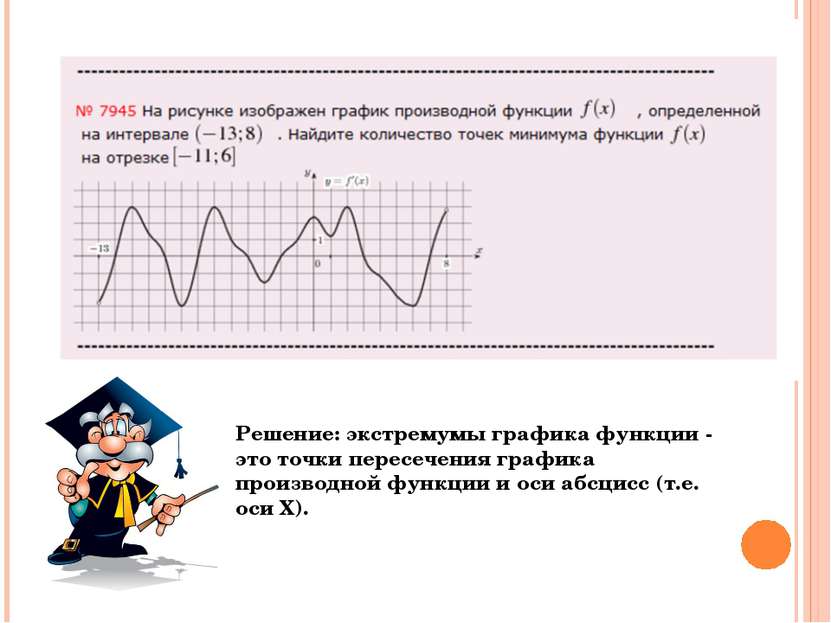
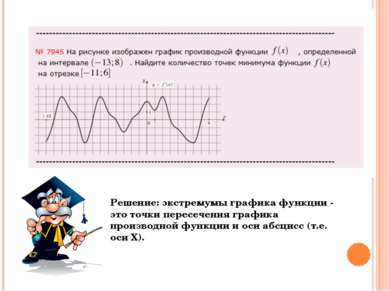Решение: экстремумы графика функции - это точки пересечения графика производной функции и оси абсцисс (т.е. оси Х).
Cлайд 7
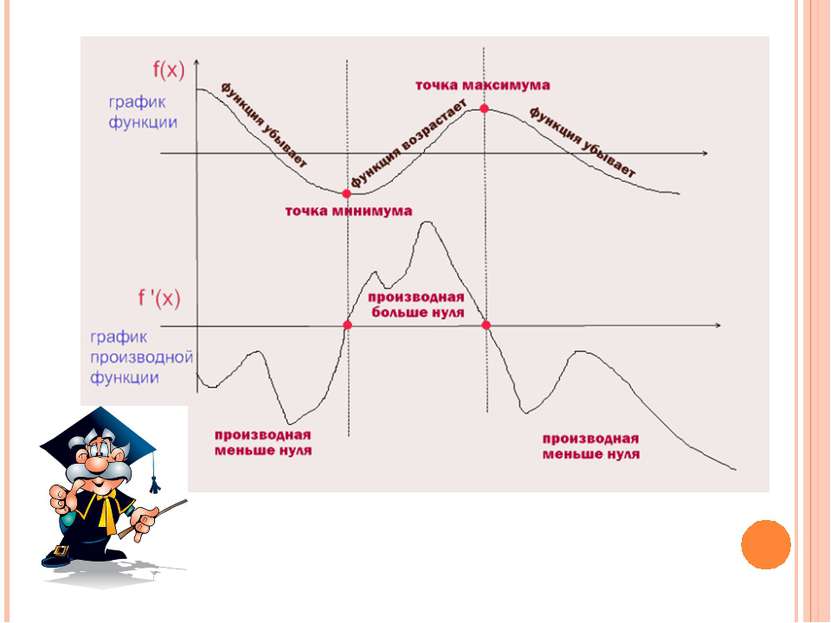
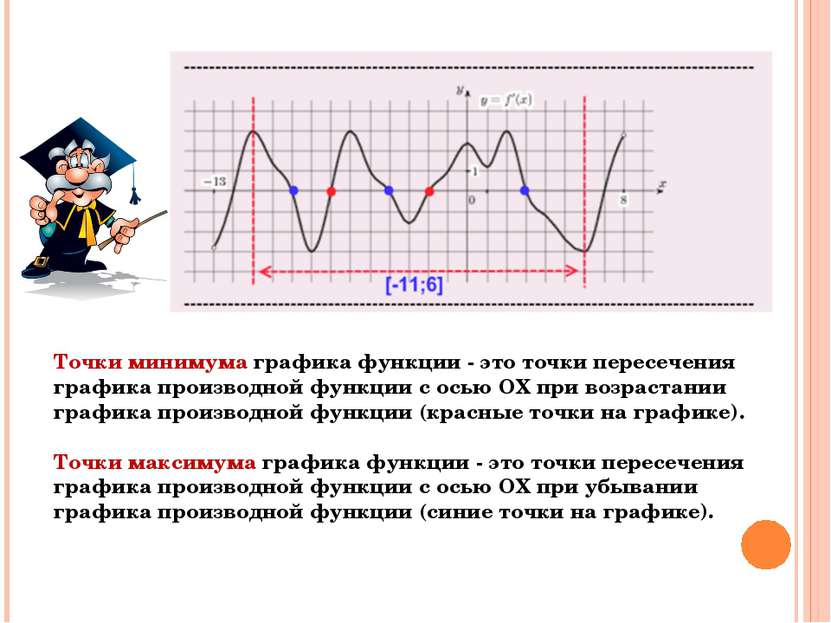
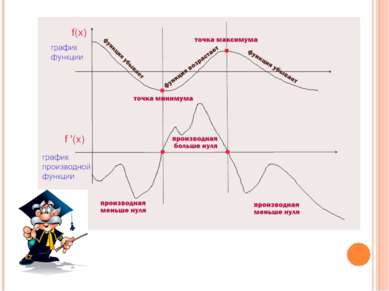
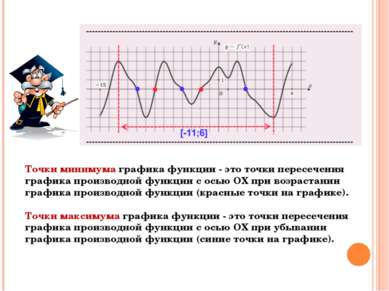Точки минимума графика функции - это точки пересечения графика производной функции с осью ОХ при возрастании графика производной функции (красные точки на графике). Точки максимума графика функции - это точки пересечения графика производной функции с осью ОХ при убывании графика производной функции (синие точки на графике).
Cлайд 8
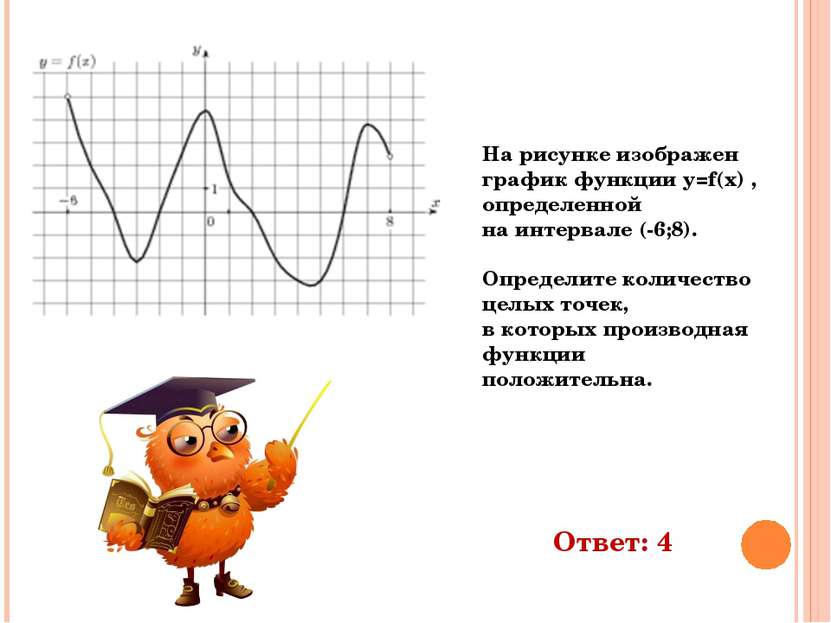
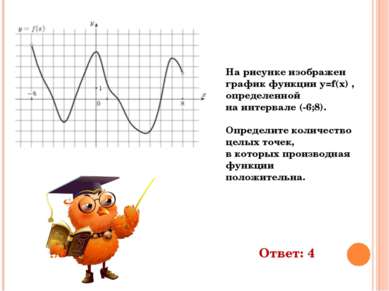На рисунке изображен график функции y=f(x) , определенной на интервале (-6;8). Определите количество целых точек, в которых производная функции положительна. Ответ: 4
Cлайд 9
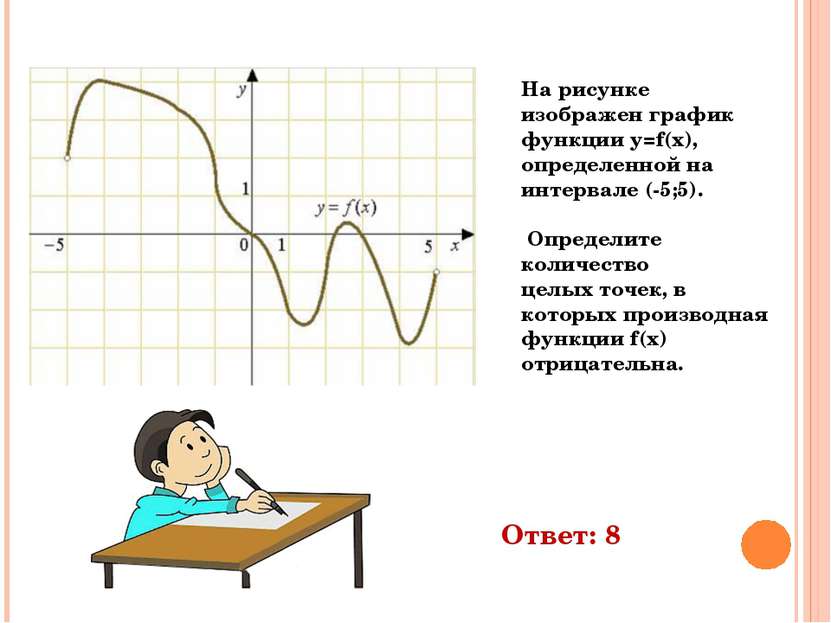
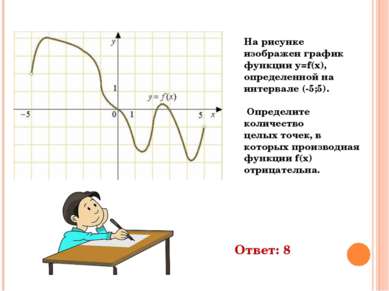На рисунке изображен график функции y=f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции f(x) отрицательна. Ответ: 8
Cлайд 10
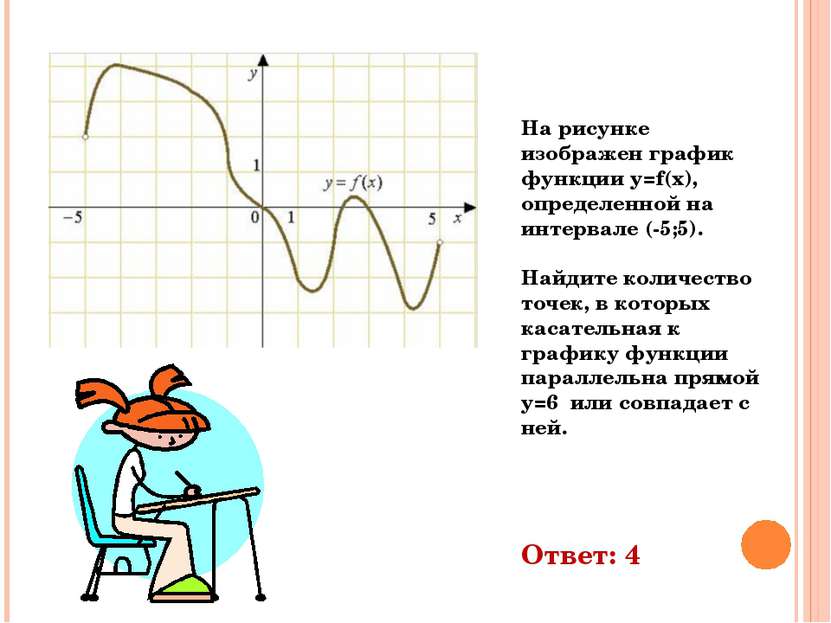
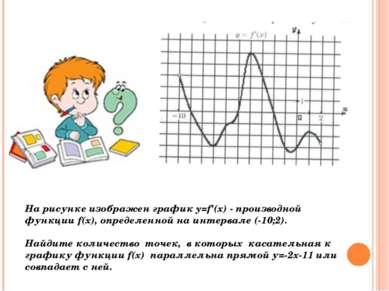
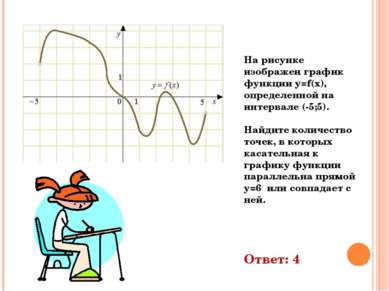На рисунке изображен график функции y=f(x), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=6 или совпадает с ней. Ответ: 4
Cлайд 11
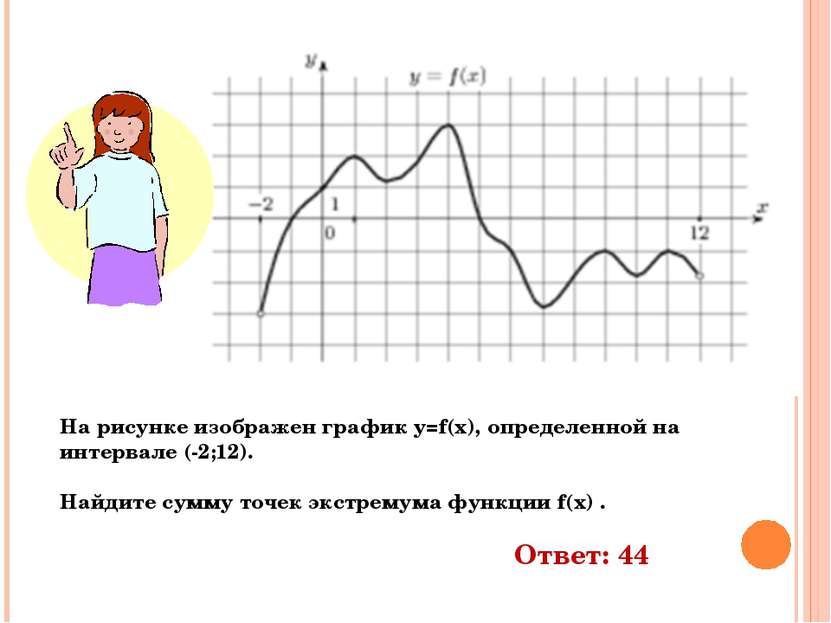
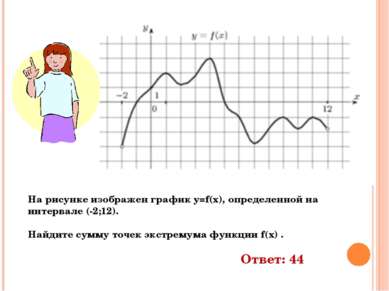На рисунке изображен график y=f(x), определенной на интервале (-2;12). Найдите сумму точек экстремума функции f(x) . Ответ: 44
Cлайд 12
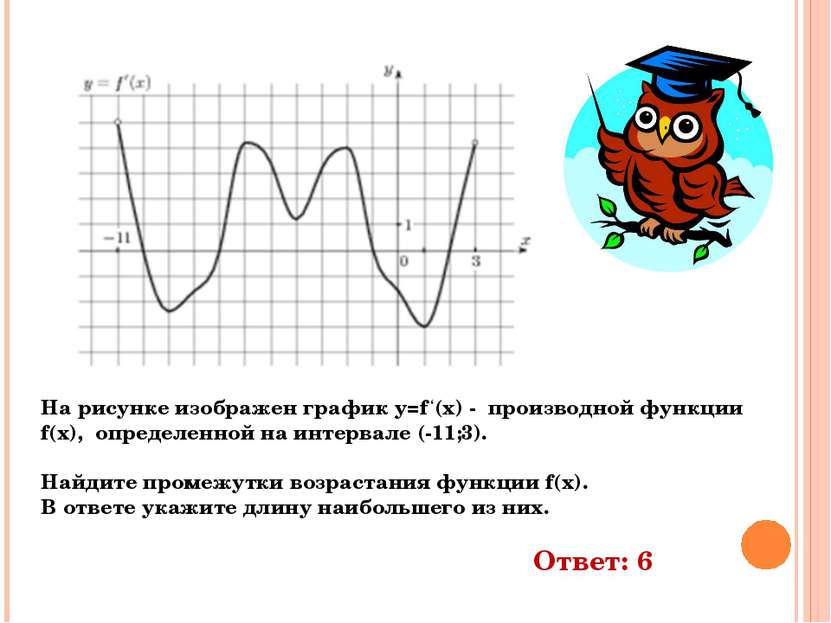
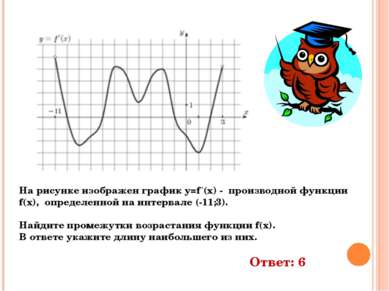На рисунке изображен график y=f ‘(x) - производной функции f(x), определенной на интервале (-11;3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них. Ответ: 6
Cлайд 13
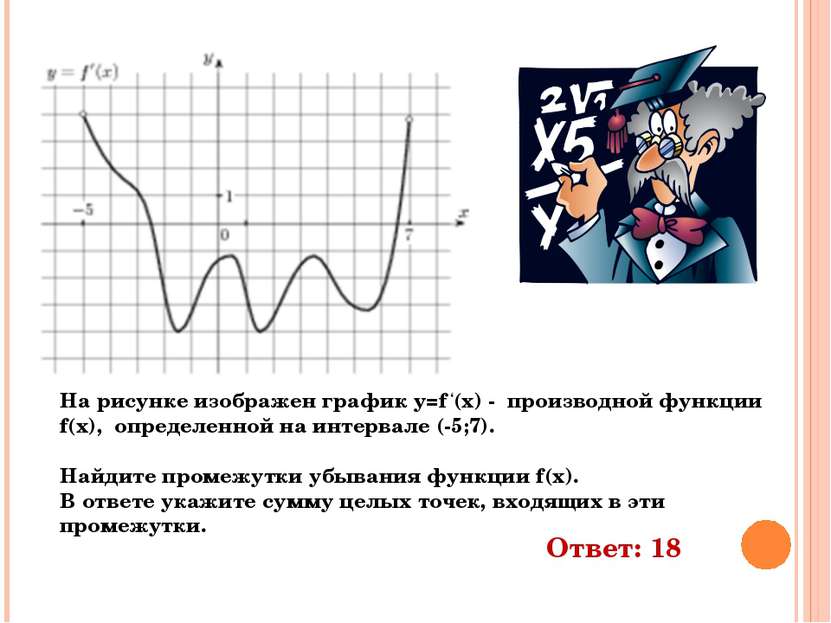
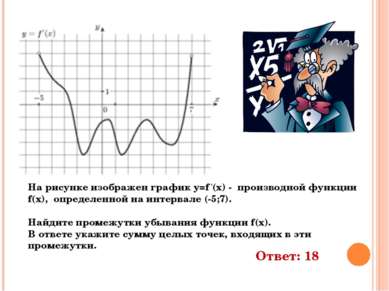На рисунке изображен график y=f ‘(x) - производной функции f(x), определенной на интервале (-5;7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки. Ответ: 18
Cлайд 14
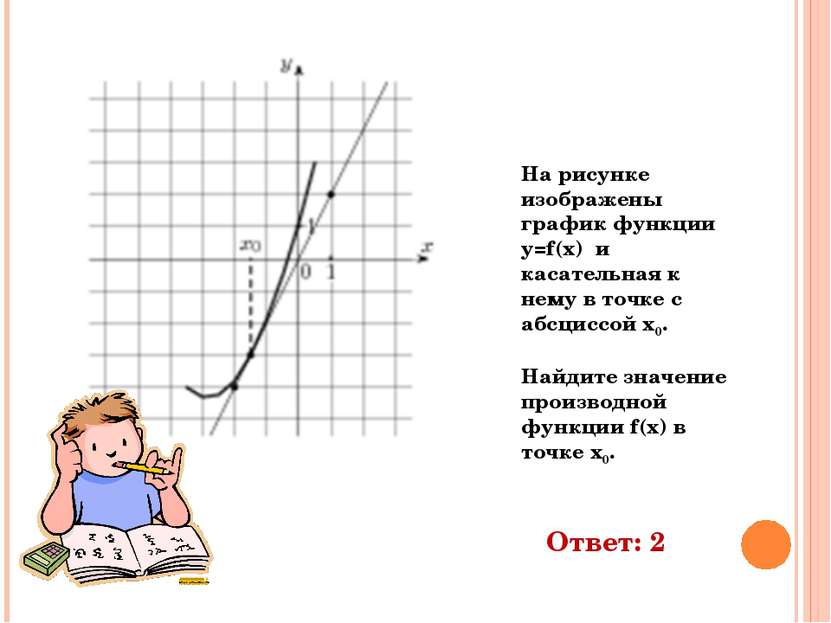
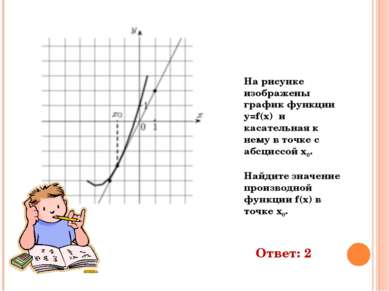На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0. Ответ: 2
Cлайд 15
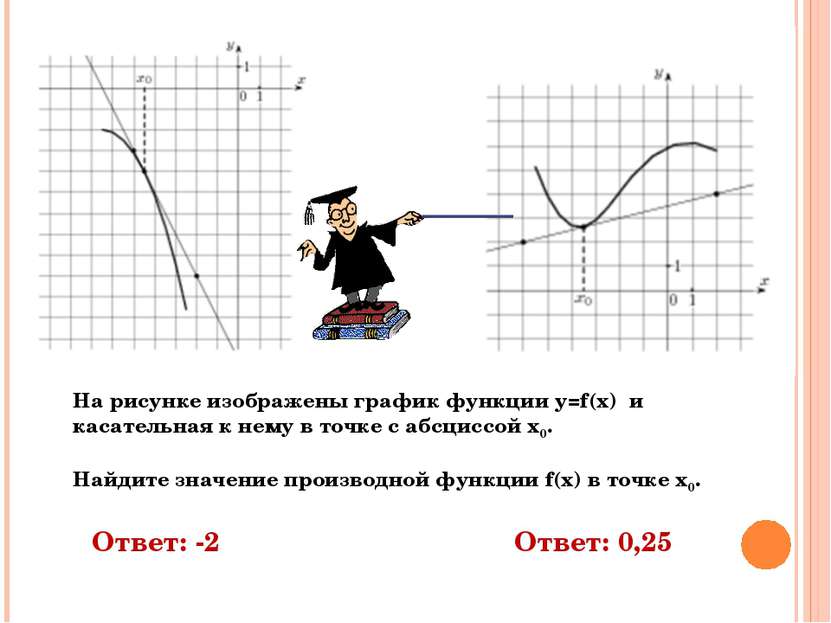
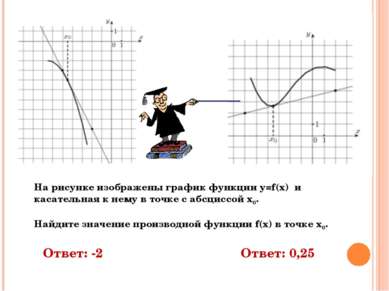Ответ: -2 Ответ: 0,25 На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
Cлайд 16
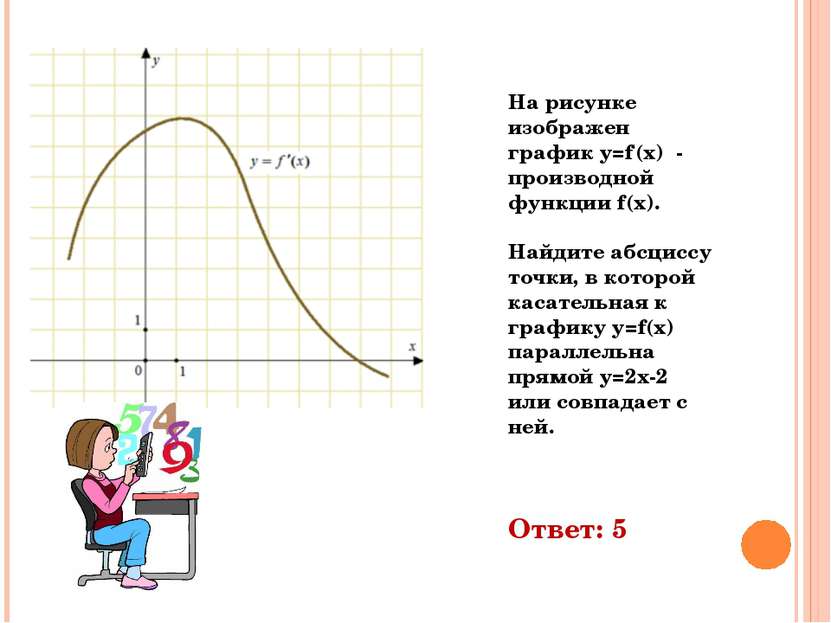
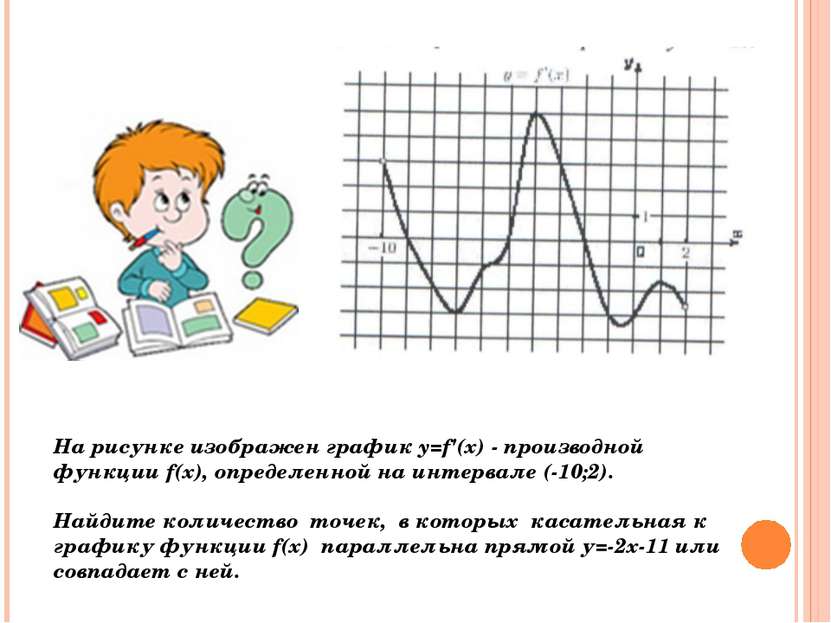
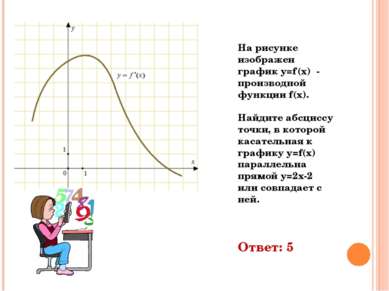На рисунке изображен график y=f‘(x) - производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y=f(x) параллельна прямой y=2x-2 или совпадает с ней. Ответ: 5
Cлайд 17
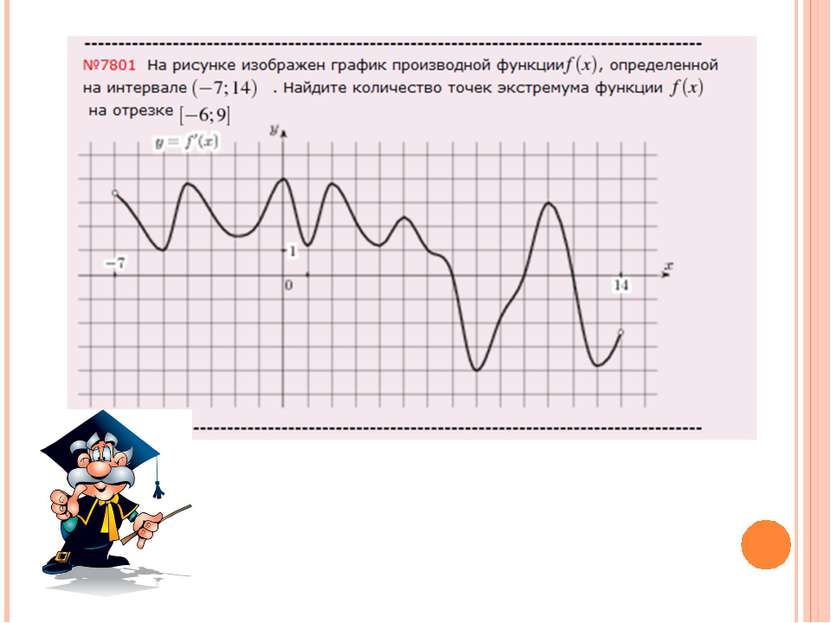
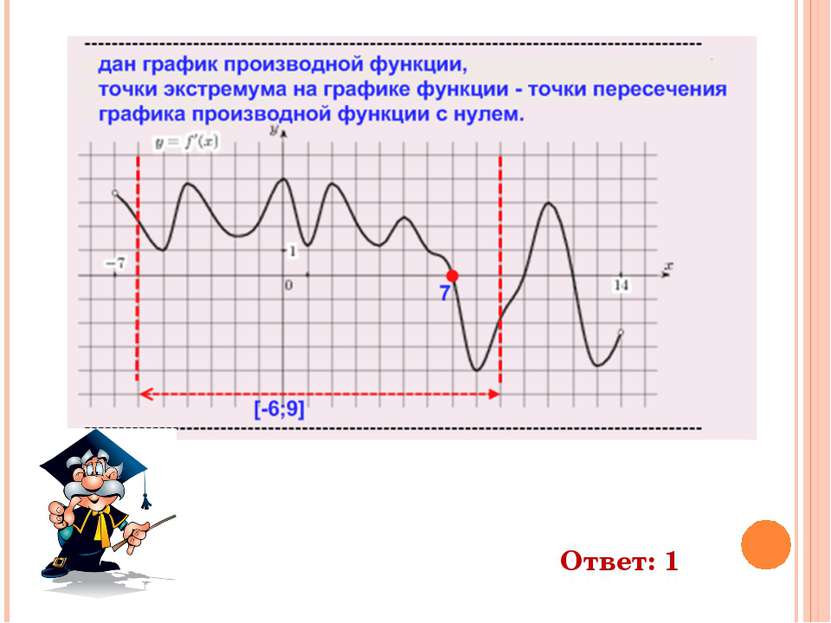
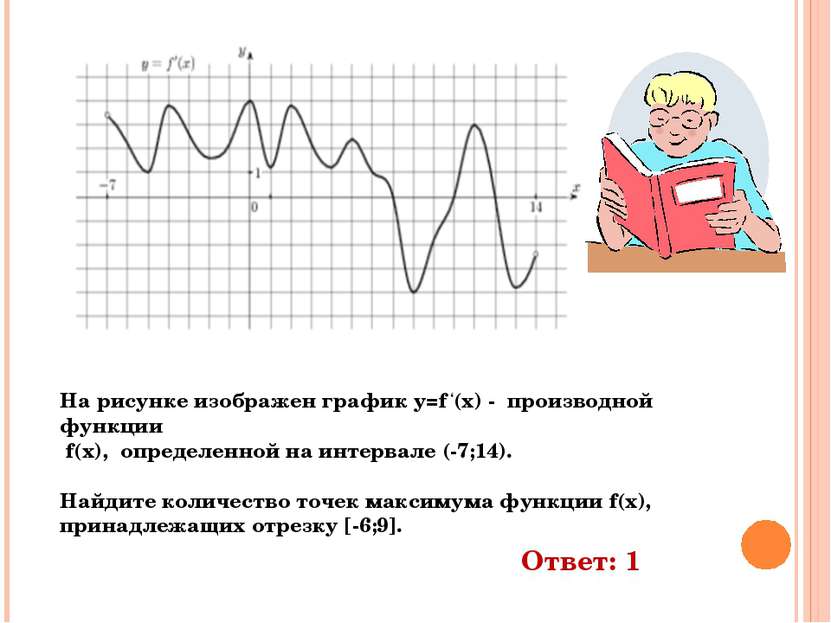
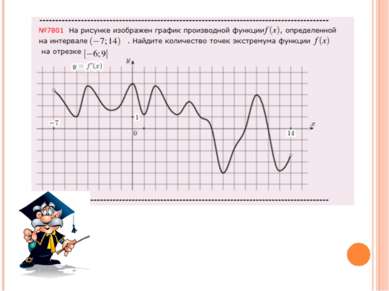
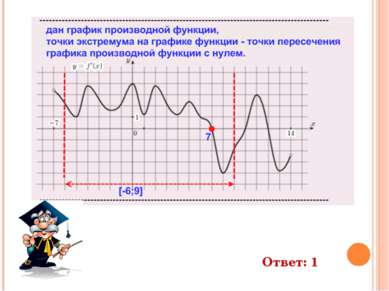
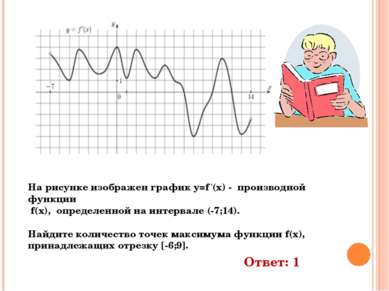На рисунке изображен график y=f ‘(x) - производной функции f(x), определенной на интервале (-7;14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;9]. Ответ: 1
Cлайд 18
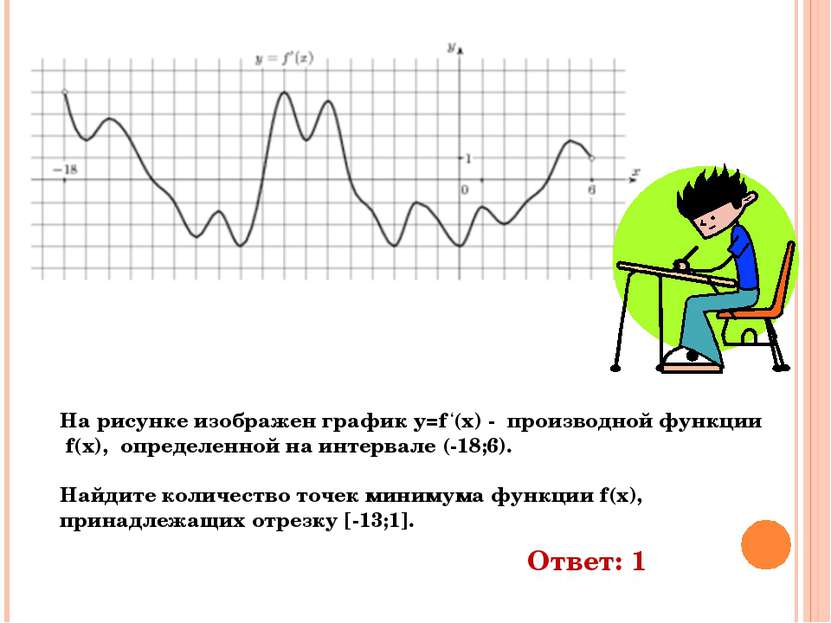
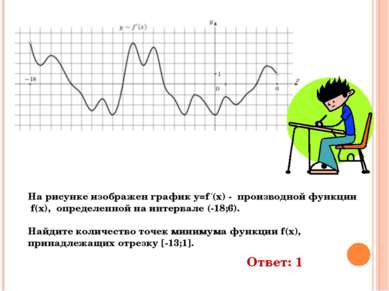На рисунке изображен график y=f ‘(x) - производной функции f(x), определенной на интервале (-18;6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13;1]. Ответ: 1
Cлайд 19
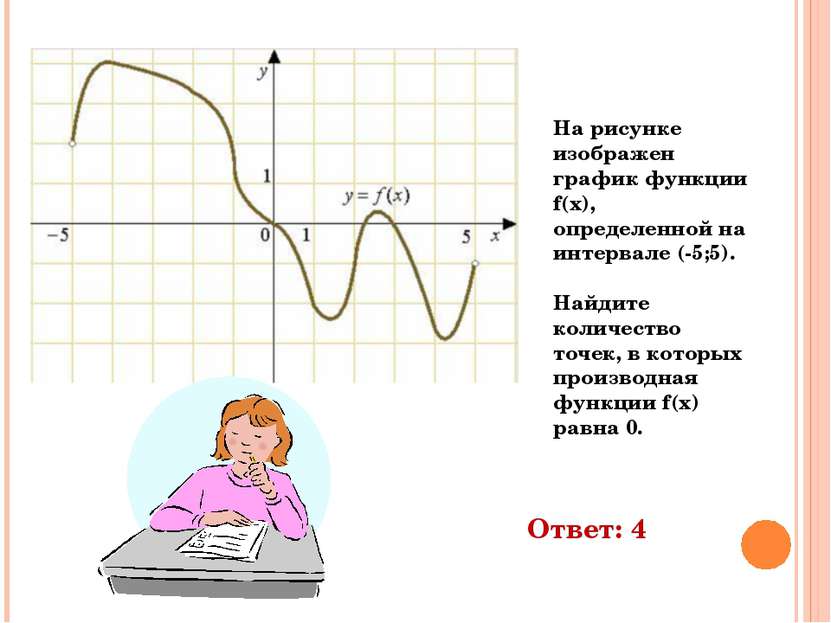
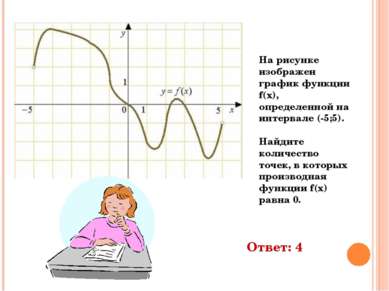На рисунке изображен график функции f(x), определенной на интервале (-5;5). Найдите количество точек, в которых производная функции f(x) равна 0. Ответ: 4
Cлайд 20
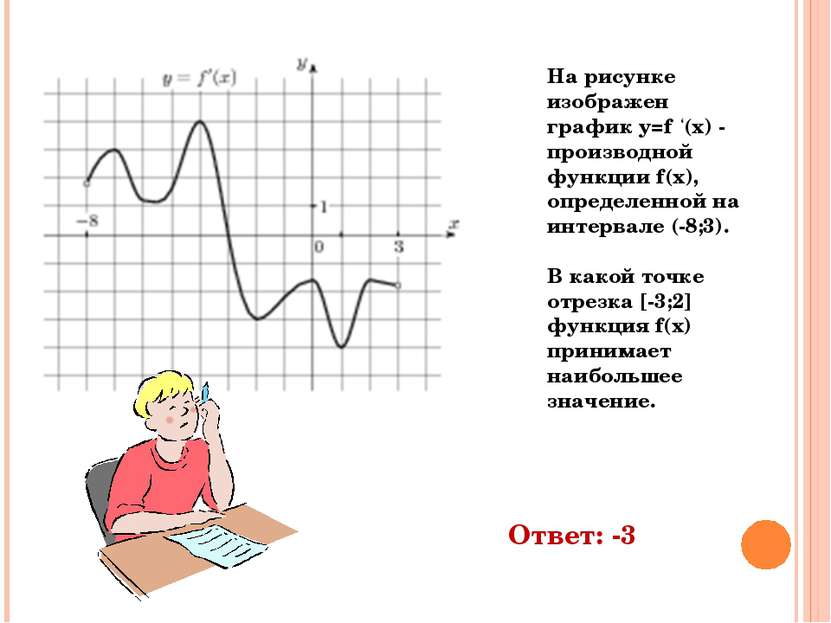
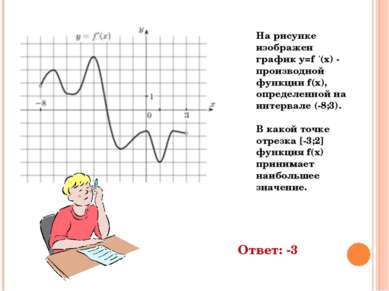На рисунке изображен график y=f ‘(x) - производной функции f(x), определенной на интервале (-8;3). В какой точке отрезка [-3;2] функция f(x) принимает наибольшее значение. Ответ: -3
Cлайд 21
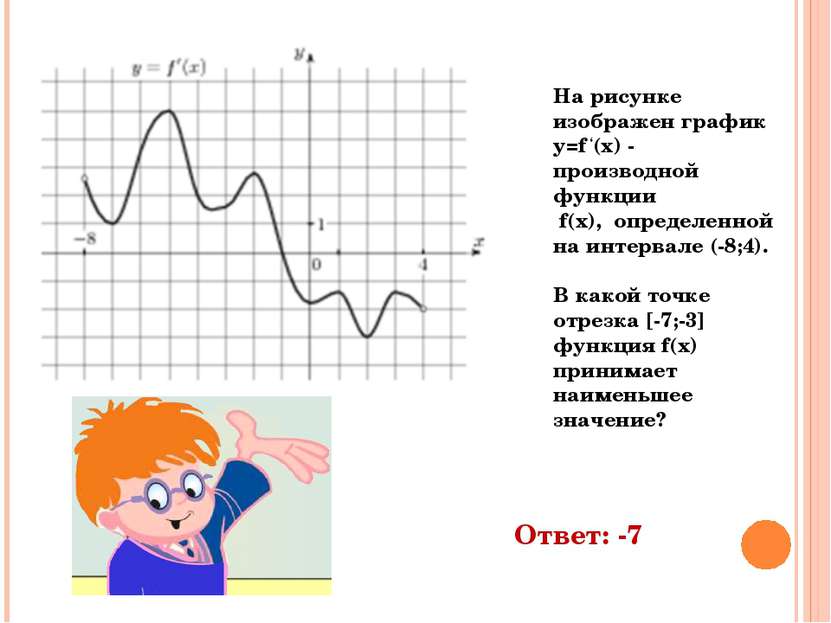
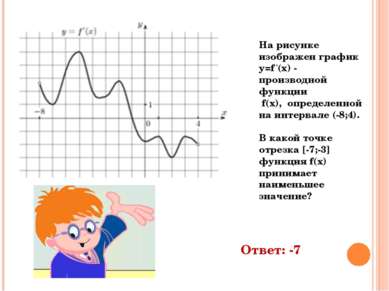На рисунке изображен график y=f ‘(x) - производной функции f(x), определенной на интервале (-8;4). В какой точке отрезка [-7;-3] функция f(x) принимает наименьшее значение? Ответ: -7
Cлайд 22
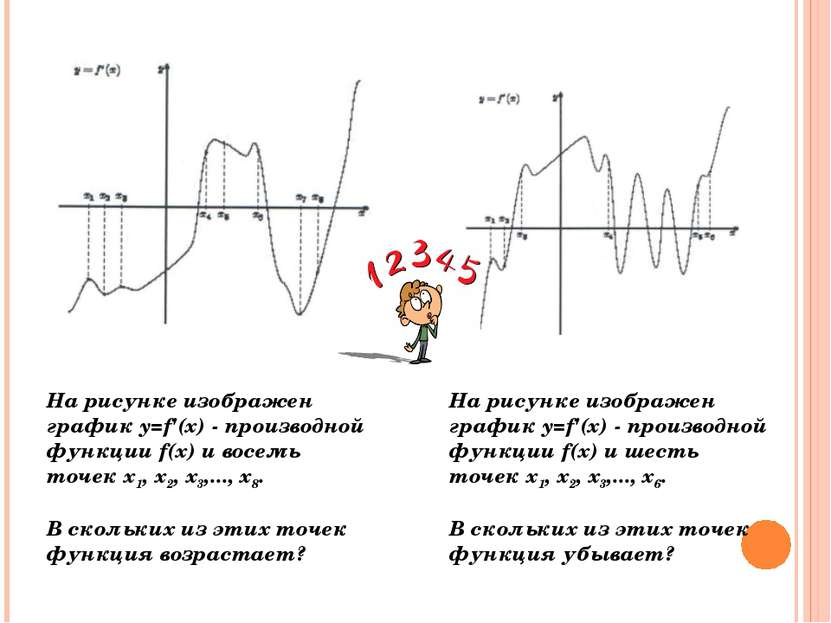
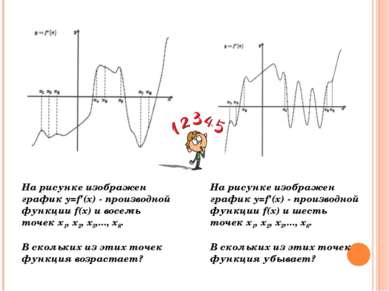На рисунке изображен график y=f'(x) - производной функции f(x) и восемь точек х1, х2, х3,..., х8. В скольких из этих точек функция возрастает? На рисунке изображен график y=f'(x) - производной функции f(x) и шесть точек х1, х2, х3,..., х6. В скольких из этих точек функция убывает?
Cлайд 23
На рисунке изображен график y=f'(x) - производной функции f(x), определенной на интервале (-10;2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой у=-2х-11 или совпадает с ней.
Cлайд 24
Спасибо за внимание!
