X
Код презентации скопируйте его
Геометрические паркеты
Скачать эту презентацию
Презентация на тему Геометрические паркеты
Скачать эту презентациюCлайд 1
Геометрическиепаркеты Выполнила: ученица 9 класса МОУ «Бестужевская общеобразовательная средняя школа» Ожигина Ольга Районная учебно-исследовательская конференция учащихся «Юность Устьи».
Cлайд 2
Цель: подробно изучить паркеты из многоугольников, правильных многоугольников и произвольных фигур. Гипотеза: количество паркетов из правильных многоугольников бесчисленное множество.
Cлайд 3
Слово паркет имеет благородное французское происхождение, которое в средние века обозначало небольшой парк, немного спустя – часть зала покрытую ковром.
Cлайд 4
В толковом словаре Ожегова С. И. паркет – это планки из твердых пород дерева для покрытия полов, а также само покрытие. В математике паркетом называется разбиение плоскости на многоугольники, при котором каждые два многоугольника либо не пересекаются, либо имеют ровно одну общую вершину, либо имеют одну общую сторону. Паркетом называется «замощение» плоскости повторяющимися фигурами без пропусков и перекрытий.
Cлайд 5
Паркет называется правильным, если он состоит из правильных многоугольников.
Cлайд 6
Паркет из квадратов
Cлайд 7
Паркет из шестиугольников.
Cлайд 8
Паркет из правильных треугольников.
Cлайд 9
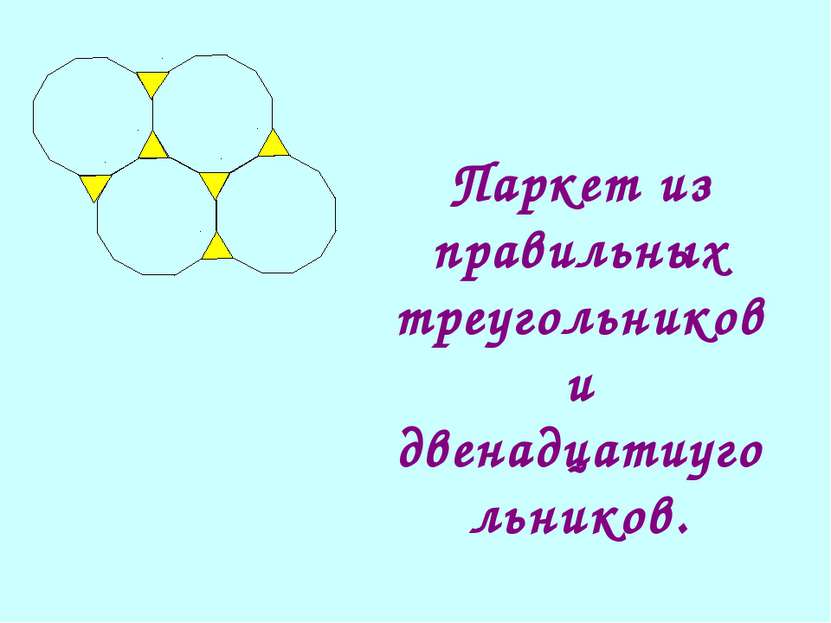
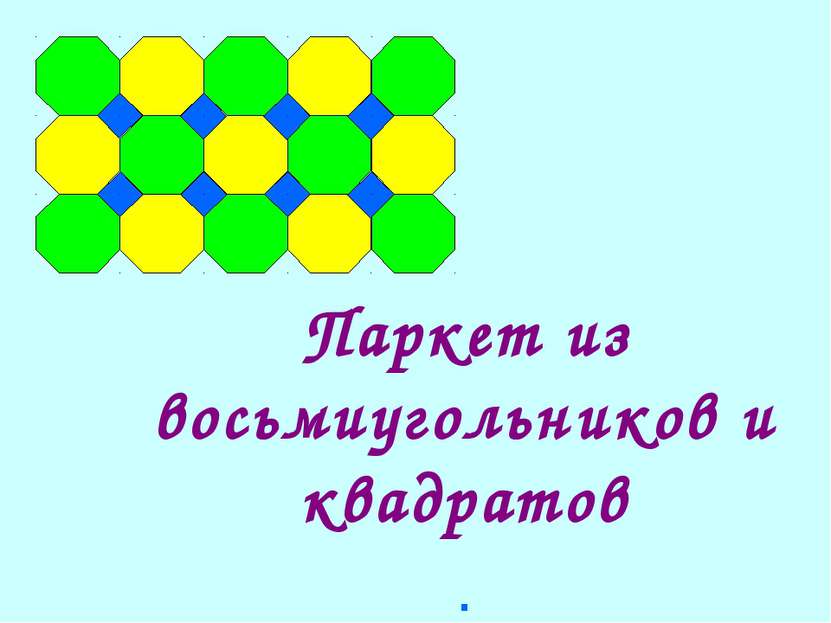
Паркет называется полуправильным, ели он состоит из правильных многоугольников (возможно с разным числом сторон), одинаково расположенных вокруг каждой вершины.
Cлайд 10
Паркет из шестиугольника и треугольников.
Cлайд 11
Паркет из квадратов и правильных треугольников.
Cлайд 12
Паркет из квадратов и правильных треугольников.
Cлайд 13
Из правильных шестиугольников и треугольников.
Cлайд 14
Паркет из квадратов и правильных треугольников и шестиугольников.
Cлайд 15
Паркет из правильных треугольников и двенадцатиугольников.
Cлайд 16
Паркет из квадратов, шестиугольников и двенадцатиугольников
Cлайд 17
Паркет из восьмиугольников и квадратов .
Cлайд 18
Некоторые определения паркета не ограничиваются многоугольниками; в этом случае паркетом называется покрытие плоскости без пропусков и перекрытий заданными фигурами.
Cлайд 19
Первый способ. Паркет, полученный из правильных шестиугольников.
Cлайд 20
Второй способ. Паркет, полученный в результате объединения пяти правильных треугольников.
Cлайд 21
Третий способ. Паркет, полученный объединением паркета из греческих крестов и паркета из квадратов.
Cлайд 22
Четвертый способ. Паркет, полученный с помощью параллельного переноса звездчатых многоугольников.
Cлайд 23
Паркеты, придуманные мной.
Cлайд 24
Паркеты, придуманные мной.
Cлайд 25
Спасибо за внимание!
