X
Код презентации скопируйте его
Определение синуса, косинуса, тангенса и котангенса углов поворота
Скачать эту презентацию
Презентация на тему Определение синуса, косинуса, тангенса и котангенса углов поворота
Скачать эту презентациюCлайд 1
Определение синуса, косинуса, тангенса и котангенса углов поворота. Алгебра и начала анализа, 10 класс Воробьев Леонид Альбертович, г.Минск
Cлайд 2
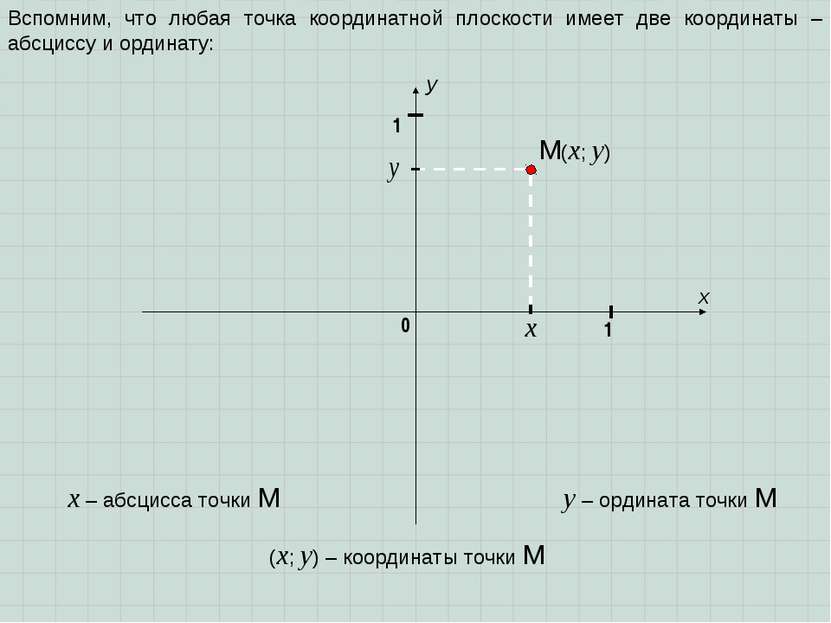
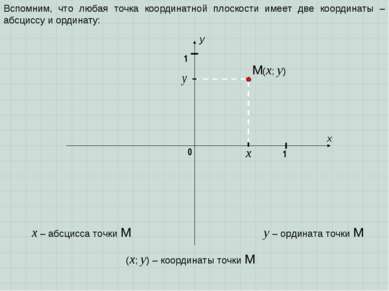x y 1 0 1 Вспомним, что любая точка координатной плоскости имеет две координаты – абсциссу и ординату: y – ордината точки M x – абсцисса точки M M(x; y) (x; y) – координаты точки M
Cлайд 3
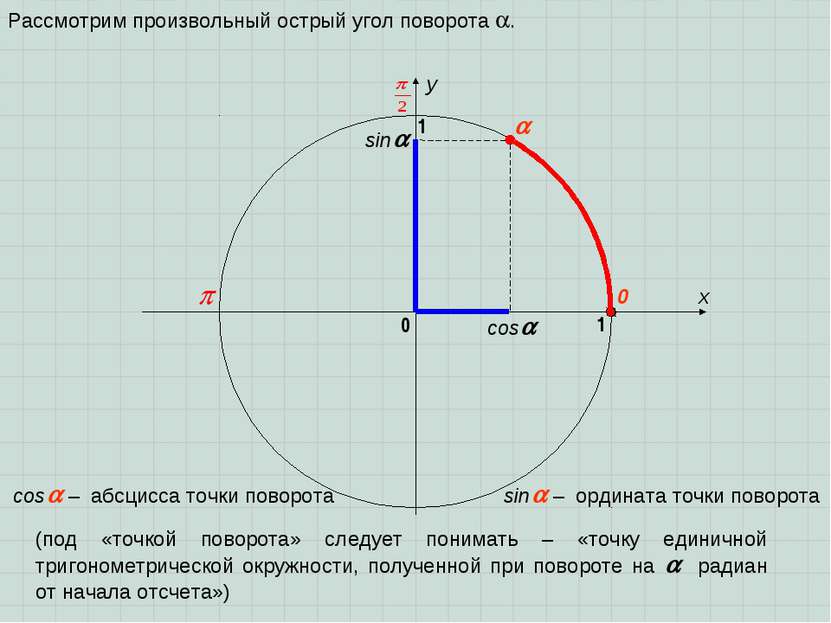
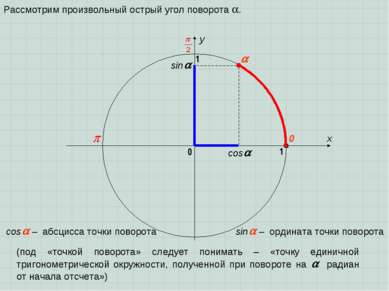sin cos x y 0 1 0 1 sin – ордината точки поворота cos – абсцисса точки поворота (под «точкой поворота» следует понимать – «точку единичной тригонометрической окружности, полученной при повороте на радиан от начала отсчета») Рассмотрим произвольный острый угол поворота .
Cлайд 4
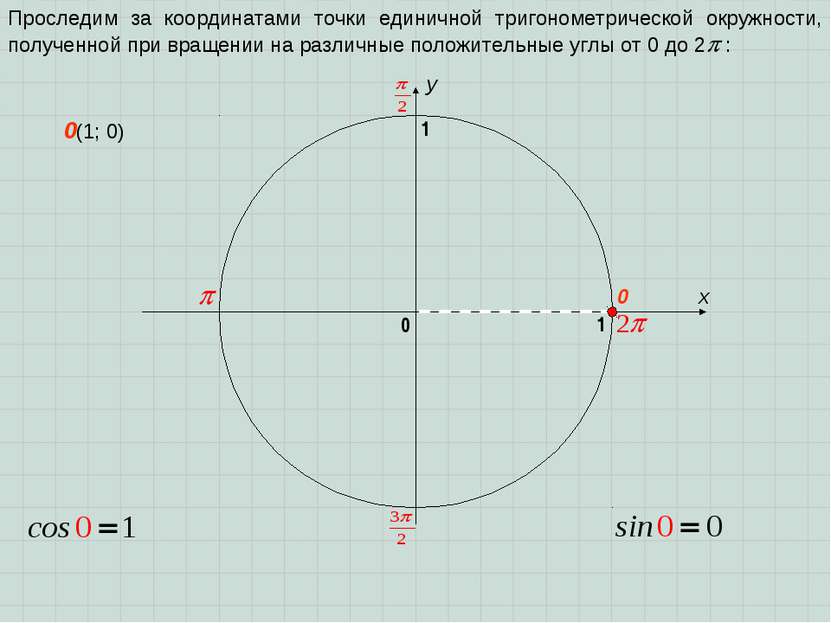
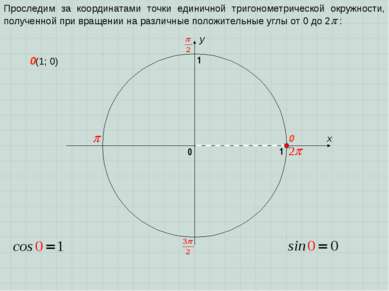x y 0 1 0 1 Проследим за координатами точки единичной тригонометрической окружности, полученной при вращении на различные положительные углы от 0 до 2 : 0(1; 0)
Cлайд 5
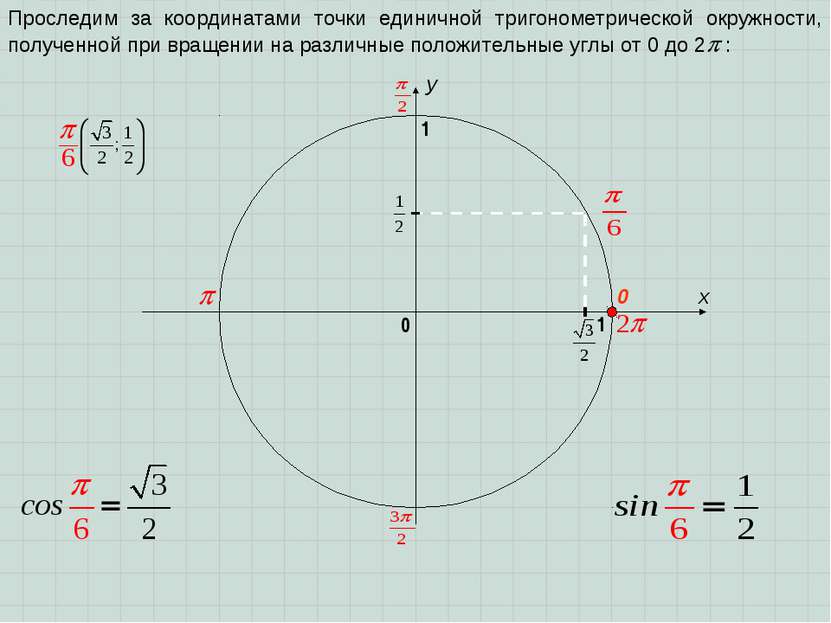
x y 0 1 0 1 Проследим за координатами точки единичной тригонометрической окружности, полученной при вращении на различные положительные углы от 0 до 2 :
Cлайд 6
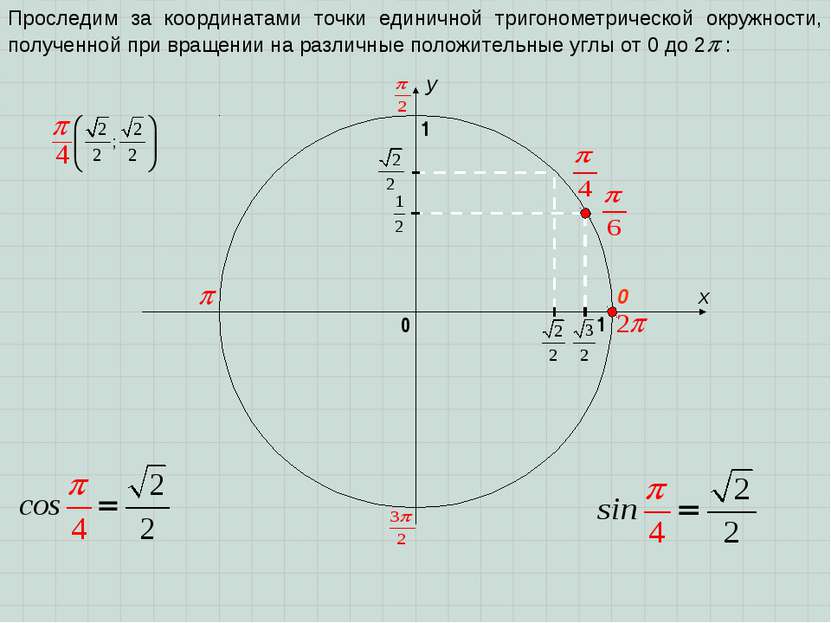
x y 0 1 0 1 Проследим за координатами точки единичной тригонометрической окружности, полученной при вращении на различные положительные углы от 0 до 2 :
Cлайд 7
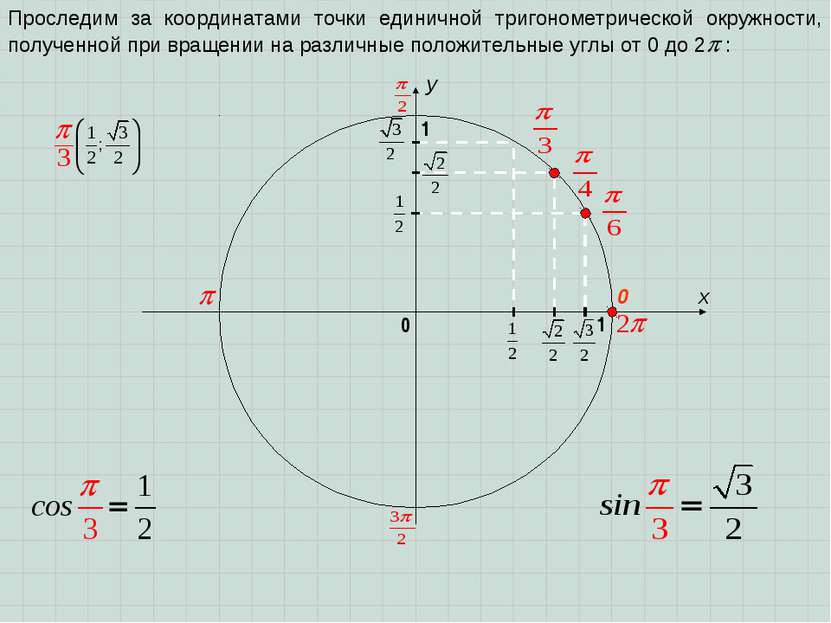
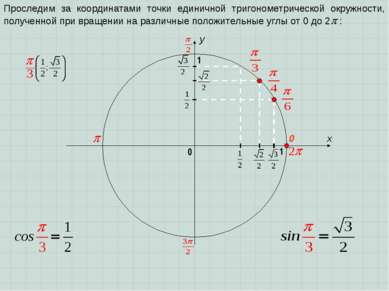x y 0 1 0 1 Проследим за координатами точки единичной тригонометрической окружности, полученной при вращении на различные положительные углы от 0 до 2 :
Cлайд 8
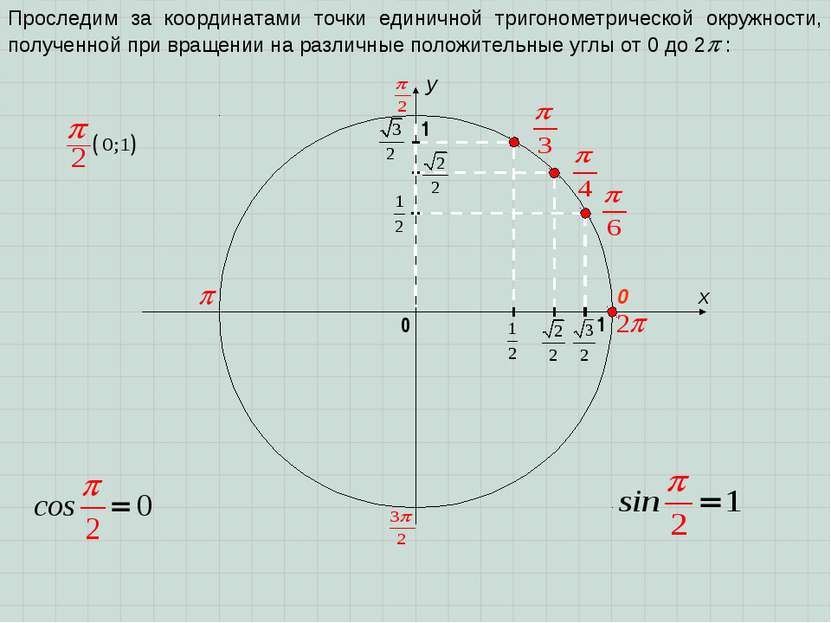
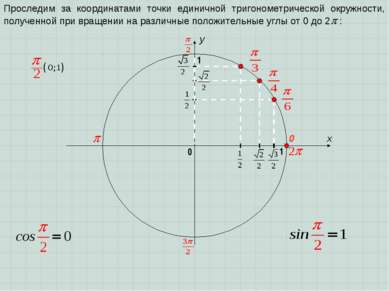x y 0 1 0 1 Проследим за координатами точки единичной тригонометрической окружности, полученной при вращении на различные положительные углы от 0 до 2 :
Cлайд 9
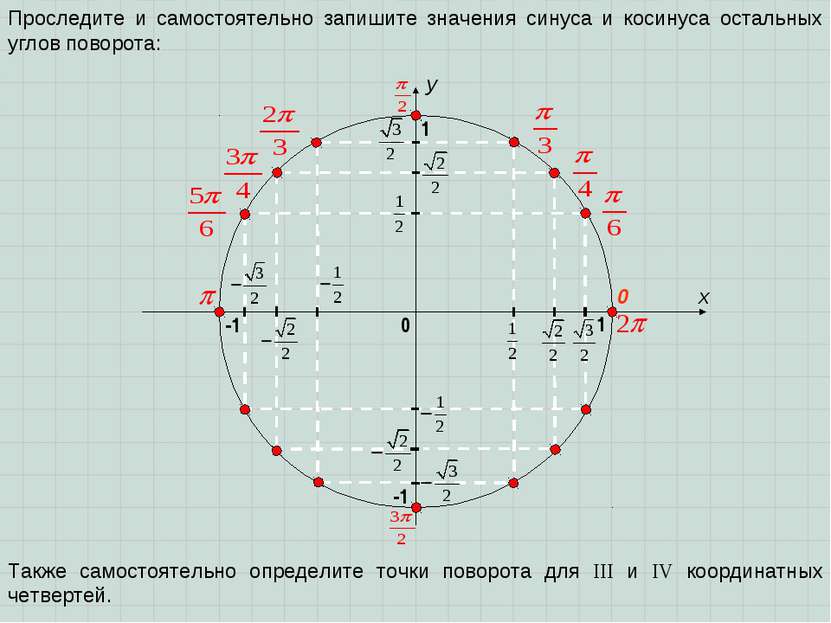
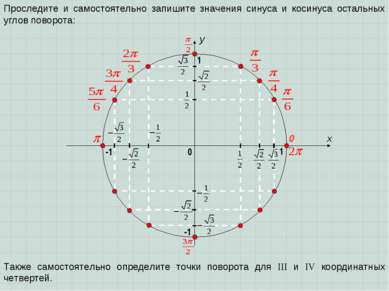x y 0 1 0 1 Проследите и самостоятельно запишите значения синуса и косинуса остальных углов поворота: -1 -1 Также самостоятельно определите точки поворота для III и IV координатных четвертей.
Cлайд 10
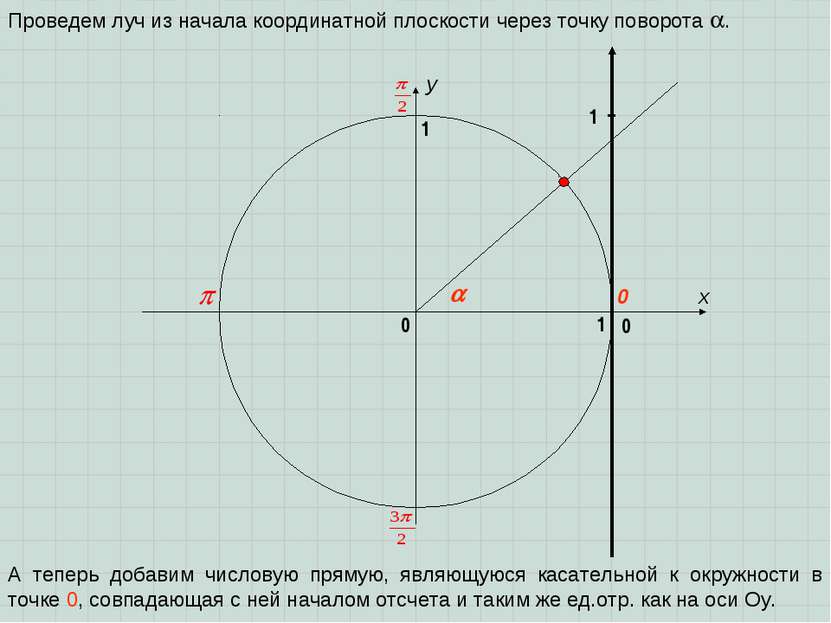
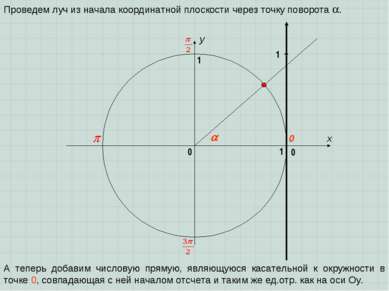x y 0 1 0 1 Проведем луч из начала координатной плоскости через точку поворота . А теперь добавим числовую прямую, являющуюся касательной к окружности в точке 0, совпадающая с ней началом отсчета и таким же ед.отр. как на оси Оу. 1 0
Cлайд 11
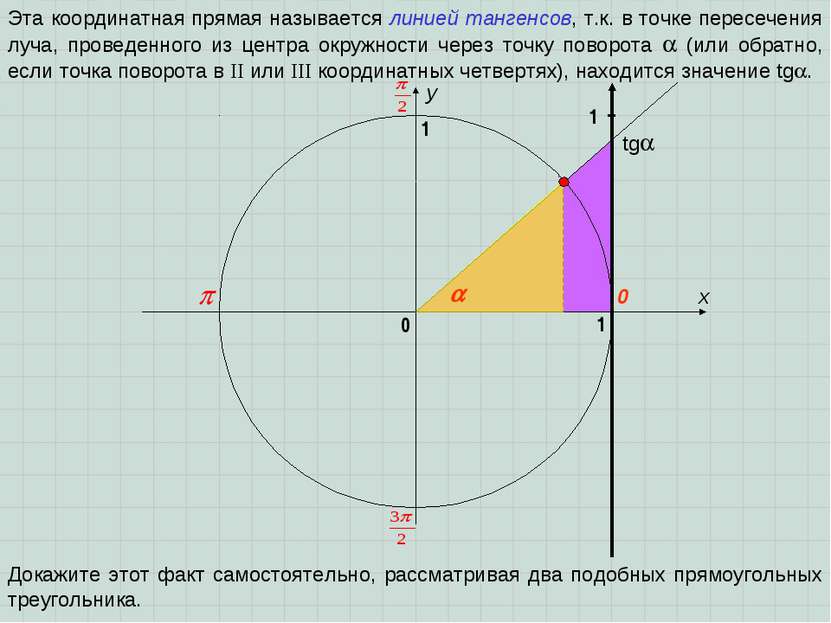
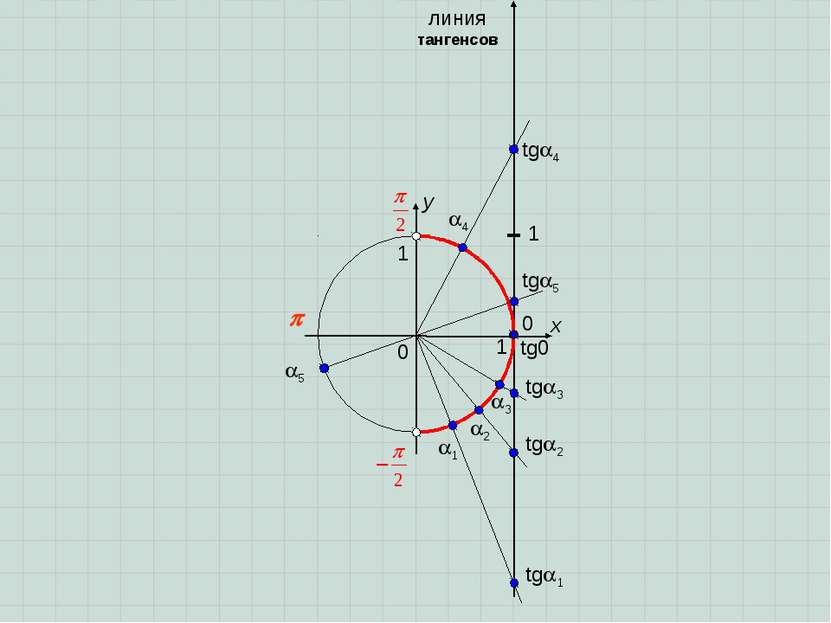
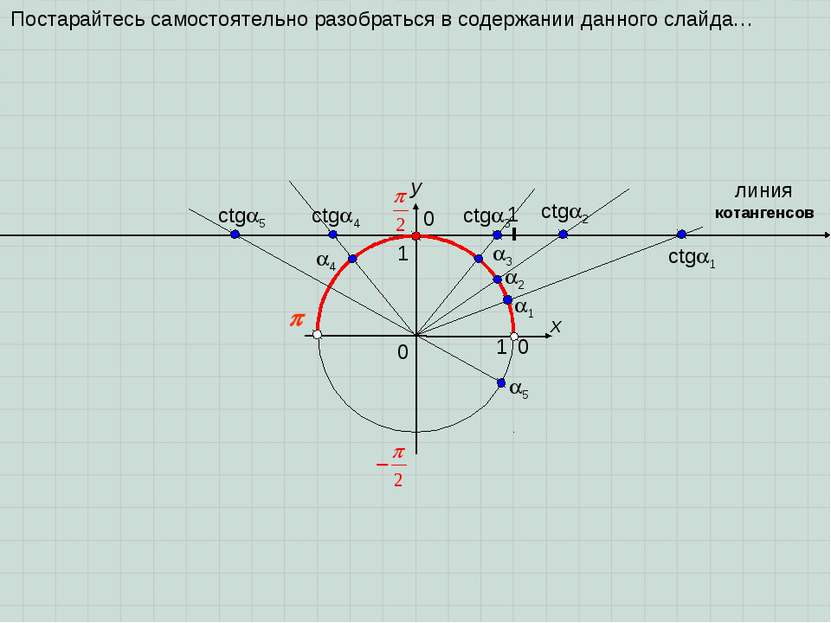
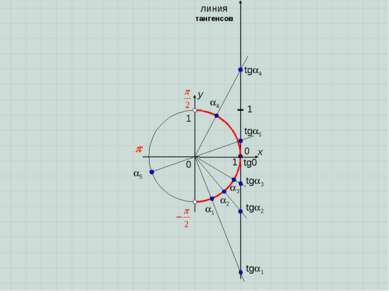
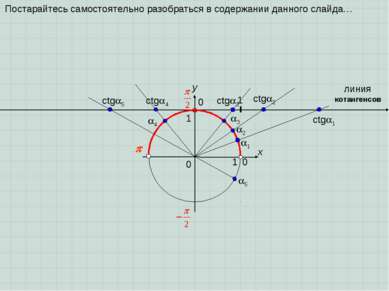
x y 0 1 0 1 Эта координатная прямая называется линией тангенсов, т.к. в точке пересечения луча, проведенного из центра окружности через точку поворота (или обратно, если точка поворота в II или III координатных четвертях), находится значение tg . Докажите этот факт самостоятельно, рассматривая два подобных прямоугольных треугольника. 1 tg
Cлайд 12
0 x y 0 1 1 1 2 3 линия тангенсов 1 tg 1 tg 2 tg 3 4 tg 4 5 tg 5 tg0
Cлайд 13
0 x y 0 1 1 1 2 3 1 ctg 2 ctg 3 линия котангенсов ctg 1 0 4 ctg 4 5 ctg 5 Постарайтесь самостоятельно разобраться в содержании данного слайда…
Cлайд 14
Итогом всей предыдущей работы может являться следующий чертеж: Выполните его аккуратно в своих тетрадях!
