X
Код презентации скопируйте его
Способы нахождения корней многочленов
Скачать эту презентацию
Презентация на тему Способы нахождения корней многочленов
Скачать эту презентациюCлайд 1
Cлайд 2
Рассмотреть решение квадратных, кубических и биквадратных уравнений; Делимость многочленов; Деление многочленов с остатком; Решение алгебраических уравнений 3-й и 4-й степени; Симметрические и возвратные уравнения; формулы Виета, Горнера и Безу. Применить полученные знания при решении задач группы С, а именно С5.
Cлайд 3
D>0, то уравнение имеет два корня. D=0, то уравнение имеет один корень. D
Cлайд 4
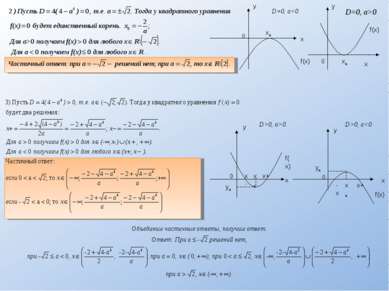
Если числа m и n таковы, что сумма равна р, а произведение равно q, то эти числа являются корнями уравнения x2+px+q=0.
Cлайд 5
Уравнения вида x4+bx2+c=0 будем называть биквадратными уравнениями. Первый способ: Биквадратное уравнение можно заменой y=x2 свести к квадратному уравнению у2+by+c=0. Второй способ.
Cлайд 6
Уравнение вида а0хn+ а1хn-1+…+ аkхn-k+…+ аkхk+…+ а1х+a0=0
Cлайд 7
Cлайд 8
Уравнения вида а0х2n+1+ а1x2n+…+ аnхn+1+ аn+1хn+…+ а2nх+a2n+1=0 называют возвратными уравнениями нечетной степени, если где λ- некоторое действительное число. Уравнения вида а0х2n+ а1x2n-1+…+ аn-1хn+1+ аnхn+…+ а2n-1х+a2n=0 называют возвратными уравнениями четной степени, если
Cлайд 9
Cлайд 10
Cлайд 11
Cлайд 12
Cлайд 13
Cлайд 14
-1 1 1 1 1 1 3 -3 -3 1 1 1 1 1 1 1 1 1 ≠0 -1 -2 0 1 2 3 ≠0 ≠0 0 -6 -4 -6 -5 -3 0 14 18 8 3 0 -11 -29 -3 0 3 ≠0 0 x1=1 x2=1 x3=1 x4=1 x5=-3
Cлайд 15
1 1 1 -1 2 2 -2 3 1 1 1 1 1 1 1 1 1 -7 -6 -5 -4 -6 -3 ≠0 ≠0 0 17 11 6 ≠0 ≠0 0 -17 -6 0 6 0 x1=1 x2=1 x3=2 x4=3
Cлайд 16
Cлайд 17
Cлайд 18
Cлайд 19
Cлайд 20
Cлайд 21
Cлайд 22
Cлайд 23
Cлайд 24
y D0. D
Cлайд 25
D>0, a>0. D>0, a0. D=0, a
Cлайд 26
В своей работе я рассмотрел, изучил и опробовал на примере одиннадцать способов решения уравнений . И я считаю, что нужно знать хотя бы самые простые способы решения уравнений высших степеней. Упростил запись и ход решения схемы Горнера. Применил полученные знания при решении задач группы С, а именно С5.
