X
Код презентации скопируйте его
Моделирование физических процессов
Скачать эту презентациюПрезентация на тему Моделирование физических процессов
Скачать эту презентациюCлайд 2
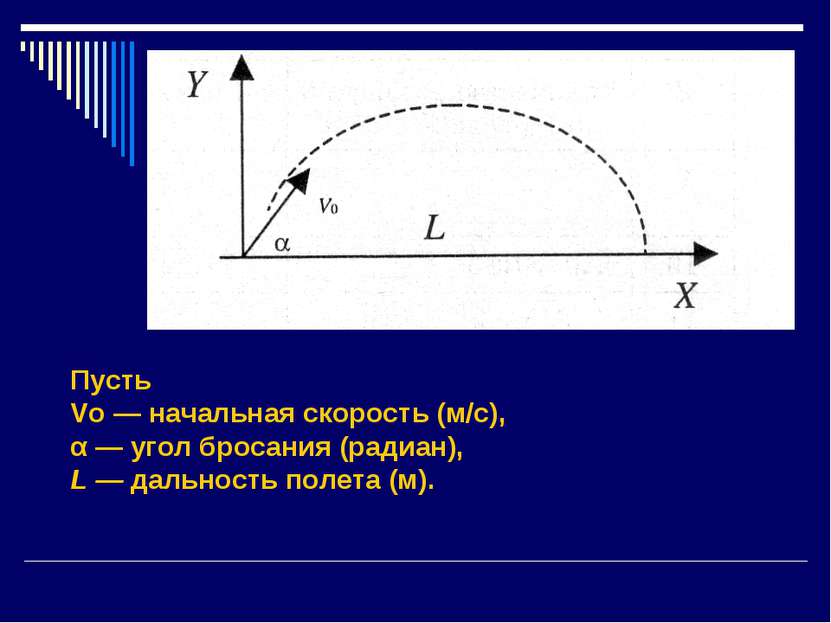
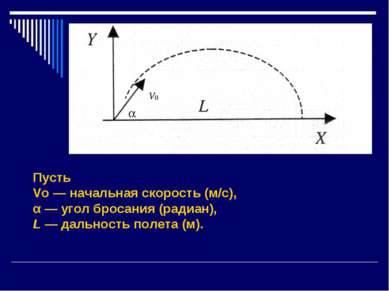
 Задача. Построить математическую модель физического процесса — движения тела, брошенного под углом к горизонту. Выяснить зависимость расстояния и времени полета тела от угла броска и начальной скорости. Угол броска и начальная скорость являются главными факторами процесса моделирования.
Задача. Построить математическую модель физического процесса — движения тела, брошенного под углом к горизонту. Выяснить зависимость расстояния и времени полета тела от угла броска и начальной скорости. Угол броска и начальная скорость являются главными факторами процесса моделирования.
Cлайд 3
 Решение. Постановка задачи. При расчетах будем использовать следующие допущения: начало системы координат расположено в точке бросания; тело движется вблизи поверхности Земли, т. е. ускорение свободного падения постоянно и равно 9,81 м/с²; сопротивление воздуха не учитывается, поэтому движение по горизонтали равномерное.
Решение. Постановка задачи. При расчетах будем использовать следующие допущения: начало системы координат расположено в точке бросания; тело движется вблизи поверхности Земли, т. е. ускорение свободного падения постоянно и равно 9,81 м/с²; сопротивление воздуха не учитывается, поэтому движение по горизонтали равномерное.
Cлайд 5
 Движение тела, брошенного под углом к горизонту, описывается следующими формулами: Vx = Vo cos α — горизонтальная составляющая начальной скорости, Vy = Vx sin α — вертикальная составляющая начальной скорости, х = Vx t — так как движение по горизонтали равномерное,
Движение тела, брошенного под углом к горизонту, описывается следующими формулами: Vx = Vo cos α — горизонтальная составляющая начальной скорости, Vy = Vx sin α — вертикальная составляющая начальной скорости, х = Vx t — так как движение по горизонтали равномерное,
Cлайд 6
 у = Vy t - – так как движение по вертикали равноускоренное с отрицательным ускорением. Искомым в этой задаче будет то значение х = L, при котором у = 0.
у = Vy t - – так как движение по вертикали равноускоренное с отрицательным ускорением. Искомым в этой задаче будет то значение х = L, при котором у = 0.
Cлайд 7
 Математическая модель. Дано: Vo — начальная скорость (м/с), α — угол бросания (радиан). Найти: L — дальность полета (м).
Математическая модель. Дано: Vo — начальная скорость (м/с), α — угол бросания (радиан). Найти: L — дальность полета (м).
Cлайд 8
 Связь: (1) L = Vx t - — дальность полета, (2) 0 = Vy t – — точка падения, (3) Vx = Vo cos α — горизонтальная проекция вектора начальной скорости, (4) Vy = Vo sin α — вертикальная проекция вектора начальной скорости, g = 9,81 — ускорение свободного падения, Vo > 0 0 < α < .
Связь: (1) L = Vx t - — дальность полета, (2) 0 = Vy t – — точка падения, (3) Vx = Vo cos α — горизонтальная проекция вектора начальной скорости, (4) Vy = Vo sin α — вертикальная проекция вектора начальной скорости, g = 9,81 — ускорение свободного падения, Vo > 0 0 < α < .
Cлайд 13
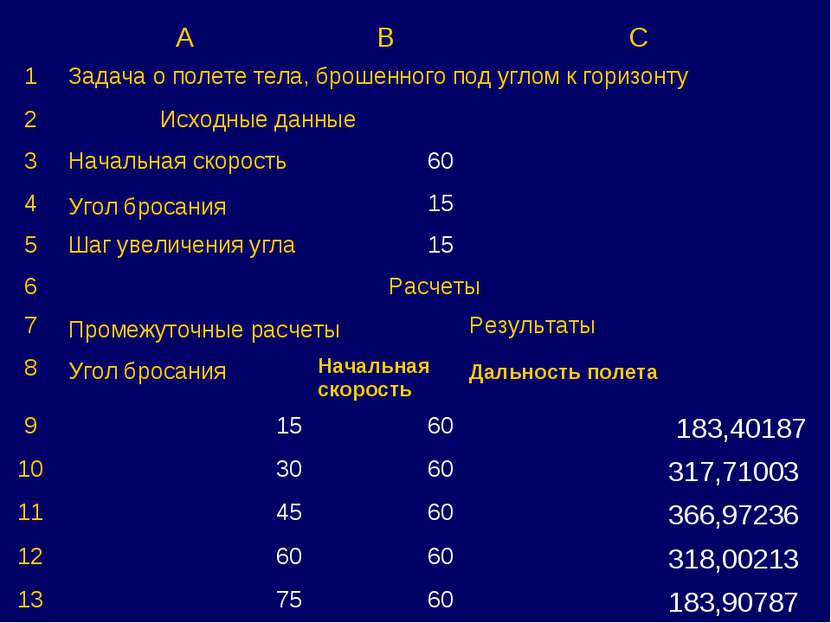
 Компьютерный эксперимент. I. Выяснить, как зависит дальность полета от угла броска. (Используем Excel) В формульном виде:
Компьютерный эксперимент. I. Выяснить, как зависит дальность полета от угла броска. (Используем Excel) В формульном виде:
Cлайд 15
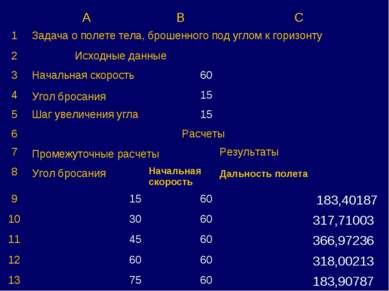 A B C 1 Задача о полете тела, брошенного под углом к горизонту 2 Исходные данные 3 Начальная скорость 60 4 Угол бросания 15 5 Шаг увеличения угла 15 6 Расчеты 7 Промежуточные расчеты Результаты 8 Угол бросания Начальная скорость Дальность полета 9 15 60 183,40187 10 30 60 317,71003 11 45 60 366,97236 12 60 60 318,00213 13 75 60 183,90787
A B C 1 Задача о полете тела, брошенного под углом к горизонту 2 Исходные данные 3 Начальная скорость 60 4 Угол бросания 15 5 Шаг увеличения угла 15 6 Расчеты 7 Промежуточные расчеты Результаты 8 Угол бросания Начальная скорость Дальность полета 9 15 60 183,40187 10 30 60 317,71003 11 45 60 366,97236 12 60 60 318,00213 13 75 60 183,90787