X
Код презентации скопируйте его
Формальная логика
Скачать эту презентацию
Презентация на тему Формальная логика
Скачать эту презентациюCлайд 1
Формальная логика Котлярова В.Ю., учитель информатики, МБОУ СОШ №1 им. Н.К.Крупской, города Нижний Тагил
Cлайд 2
Слово «ЛОГИКА» означает - совокупность правил, которым подчиняется процесс мышления Законы Логики отражают в сознании человека свойства, связи и отношения объектов окружающего мира Логика как наука позволяет строить формальные модели окружающего мира (отстраняясь от их содержательной стороны)
Cлайд 3
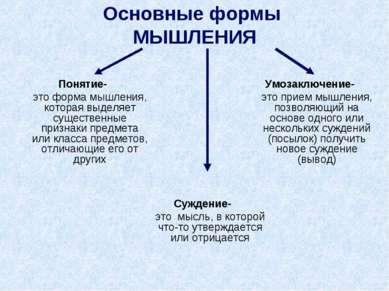Основные формы МЫШЛЕНИЯ Понятие- это форма мышления, которая выделяет существенные признаки предмета или класса предметов, отличающие его от других Суждение- это мысль, в которой что-то утверждается или отрицается Умозаключение- это прием мышления, позволяющий на основе одного или нескольких суждений (посылок) получить новое суждение (вывод)
Cлайд 4
Примеры Квадрат «Принтер предназначен для ввода информации» Ураганный ветер Доказательство теоремы «Дважды два равно четырем» Понятие Суждение ложное Понятие Умозаключение Суждение истинное
Cлайд 5
Формальная логика это наука о законах и формах мышления Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем, которые лежат в основе работы любого компьютера
Cлайд 6
Суждения в математической логике называют высказываниями или логическими выражениями Высказывание – это повествовательное предложение, о котором можно сказать, истинно оно или ложно. Примеры: Каждый ромб – параллелограмм (истинно) Каждый параллелограмм – ромб (ложно) Каждый треугольник – равнобедренный треугольник (ложно) Каждый равнобедренный треугольник – треугольник (истинно)
Cлайд 7
Сложное (составное) высказывание - получается из простых или сложных высказываний с использованием союзов «И», «ИЛИ» и частицы «НЕ» Простые ИЛИ сложные высказывания также называют логическими выражениями
Cлайд 8
Пример: Составь сложно высказывание с союзом И, ИЛИ Простое высказывание: «На улице светит солнце» Простое высказывание: «На улице пасмурная погода» Сложное высказывание с союзом «И»: «На улице светит солнце И на улице пасмурная погода» ЛОЖНО Сложное высказывание с союзом «ИЛИ»: «На улице светит солнце ИЛИ на улице пасмурная погода» ИСТИННО
Cлайд 9
Логическое выражение - это символическая запись, состоящая из логических величин (констант или переменных), объединенных логическими операциями Существуют разные варианты обозначения истинности или ложности переменных
Cлайд 10
Логические операции и их свойства
Cлайд 11
Таблица истинности - это таблица со всеми возможными значениями входных переменных и соответствующими им значениями логической функции Логическая функция - это в которой переменные принимают только два значения: логическая единица и логический нуль
Cлайд 12
Инверсия Одноместная логическая операция Частица «НЕ» Иначе называется: Логическим отрицанием Обозначение: А, А Результат ИНВЕРСИИ будет ложным, если исходное выражение истинно, и наоборот. А А 0 1 1 0
Cлайд 13
Конъюнкция Двухместная логическая операция Союз «И» Иначе называется: Логическим умножением Обозначение: А&B, А B, АxB, АB Результат КОНЪЮНКЦИИ будет истинным, тогда и только тогда, когда истинны оба исходных логических выражения одновременно. А В А&B 0 0 0 0 1 0 1 0 0 1 1 1
Cлайд 14
Дизъюнкция Двухместная логическая операция Союз «ИЛИ» Иначе называется: Логическим сложением Обозначение: АVB, А+B Результат ДИЗЪЮНКЦИИ будет истинным, тогда и только тогда, когда истинно хотя бы одно из исходных логических выражений. А В АvB 0 0 0 0 1 1 1 0 1 1 1 1
Cлайд 15
Импликация Условная двухместная логическая операция Связка «ЕСЛИ…, ТО…» Иначе называется: Логическим следованием Обозначение: А=>B Результат ИМПЛИКАЦИИ будет ложным, тогда и только тогда, когда условие истинно, а следствие ложно. А В А=>B 0 0 1 0 1 1 1 0 0 1 1 1
Cлайд 16
Эквивалентность Двухместная логическая операция Связка «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» Иначе называется: Равнозначностью Обозначение: АB Результат ЭКВИВАЛЕНТНОСТИ будет истинным, тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. А В АB 0 0 1 0 1 0 1 0 0 1 1 1
Cлайд 17
Литература Е.С.Кутугина «Арифметические и логические основы построения компьютера». Издание третье.Томск, 2007 год.
