X
Код презентации скопируйте его
Способы решения уравнений с помощью компьютера
Скачать эту презентацию
Презентация на тему Способы решения уравнений с помощью компьютера
Скачать эту презентациюCлайд 1
Способы решения уравнений с помощью компьютера. Урок информатики 11 класс Разработала: учитель информатики МБОУ г. Астрахани «СОШ№54» Кононенко Н.В.
Cлайд 2
Цели урока: расширение и систематизация знаний учащихся о применении компьютера для решения задач, способах решения алгебраических уравнений с помощью компьютера. Совершенствование навыков составления и реализации программ на языке Турбо Паскаль, навыков использования программы Excel для решения задач. Создание условий для развития исследовательской, творческой, познавательной деятельности учащихся.
Cлайд 3
Задача: решить уравнение вида Какими способами можно решить уравнение? Что значит решить уравнение аналитически? Что значит решить уравнение графически?
Cлайд 4
Из каких этапов складывается решение задач с помощью ПК? Постановка задачи Разработка формальной модели Построение компьютерной модели Компьютерный эксперимент Анализ результатов Корректировка модели
Cлайд 5
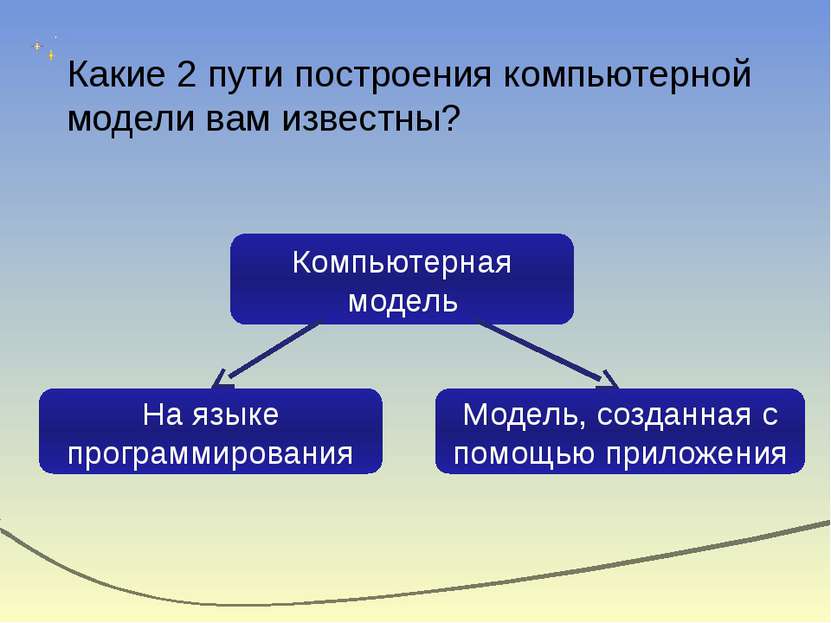
Какие 2 пути построения компьютерной модели вам известны? Компьютерная модель На языке программирования Модель, созданная с помощью приложения
Cлайд 6
Из каких этапов складывается графическое решение уравнения с помощью программы Excel? Построение таблицы значений Построение графиков функций Определение корней уравнения(точек пересечения графиков)
Cлайд 7
Решим уравнение вида sin(2*α)=0.5*(sin(α)+cos(α)) Этапы решения уравнения с помощью численных методов: отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения; вычисление корня с заданной точностью.
Cлайд 8
Численные методы приближенного вычисления корней уравнения: Метод половинного деления Метод касательных Метод хорд Метод секущих Метод хорд и касательных
Cлайд 9
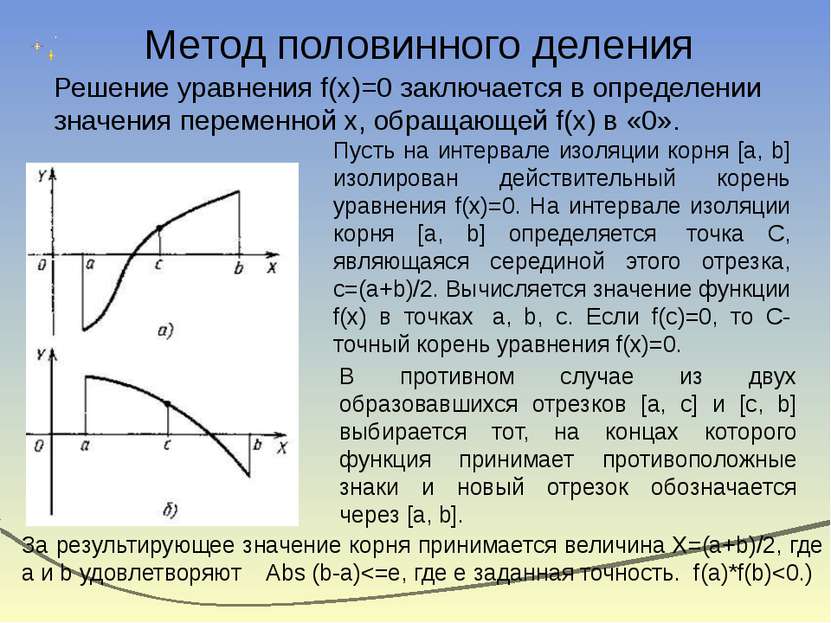
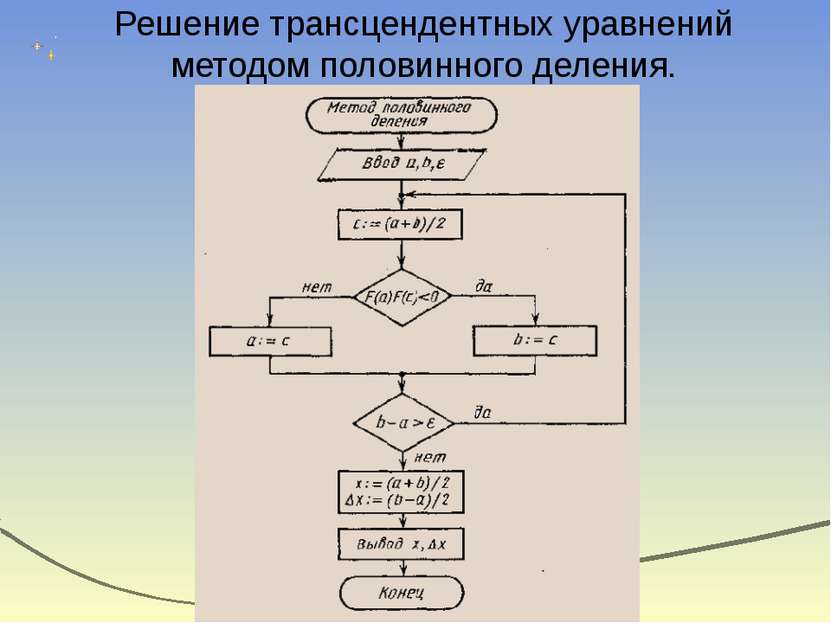
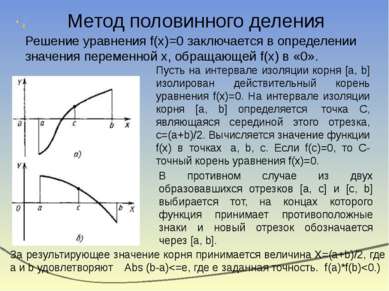Метод половинного деления Решение уравнения f(x)=0 заключается в определении значения переменной х, обращающей f(x) в «0». Пусть на интервале изоляции корня [a, b] изолирован действительный корень уравнения f(x)=0. На интервале изоляции корня [a, b] определяется точка С, являющаяся серединой этого отрезка, c=(a+b)/2. Вычисляется значение функции f(x) в точках a, b, c. Если f(c)=0, то С-точный корень уравнения f(x)=0. В противном случае из двух образовавшихся отрезков [a, c] и [c, b] выбирается тот, на концах которого функция принимает противоположные знаки и новый отрезок обозначается через [a, b]. За результирующее значение корня принимается величина X=(a+b)/2, где a и b удовлетворяют Abs (b-a)
Cлайд 10
Решение трансцендентных уравнений методом половинного деления.
Cлайд 11
Практическое закрепление. 1 группа: Отделяет корни уравнения: составляет таблицу значений функции на интервале от 0 до 1,95 с шагом 0,15 и выделяет соседние значения аргументов для которых значения функции имеют разные знаки, то есть значения аргументов между которыми находится нуль функции. 2 группа: Определяет корни графически на интервале от 0 до 1,95 с шагом 0,15. 3 группа: В среде Турбо Паскаль реализует составленную программу и определяет корни с точность 0,001.
Cлайд 12
Подведение итогов занятия Какие способы решения уравнений рассмотрели на уроке? Из каких этапов складывается графическое решение с использованием программы Excel? Какие численные методы используются для решения уравнений? В чем сущность метода половинного деления? Какой способ организации действий использован в составленной программе? В чем преимущество численных методов перед графическим методом отыскания корней? Что не учитывает программа составленная на уроке?
Cлайд 13
Домашнее задание: модернизировать программу, предусмотрев возможность отыскания интервалов, содержащих корень.
