X
Код презентации скопируйте его
Неопределённость знаний и измерение информации
Скачать эту презентацию
Презентация на тему Неопределённость знаний и измерение информации
Скачать эту презентациюCлайд 1
Верещагина Ю.Ю. МОУ СОШ с. Золотая Долина Партизанского района Приморского края
Cлайд 2
Содержательный подход к измерению информации Количество информации в сообщении зависит от того, насколько новым является это сообщение для получателя. Информации в сообщении будет тем больше, чем больше это сообщение пополняет наши знания.
Cлайд 3
Вероятностный подход Пример 1: Родители переживая за сына-студента, посылают ему телеграмму с вопросом об экзамене: «Сдал?». В ответ приходит телеграмма: «Да!». Посылая свою телеграмму, родители знали, что получат всего один из двух вариантов ответа – либо «да», либо «нет». Но какой именно, они не знали. Их неопределённость знания ответа была равна 2.
Cлайд 4
Пример 2: Человек бросает монету, загадывая, что выпадет: орёл или решка. Бросая монету, человек знает, что получит один из двух возможных вариантов. Его неопределённость знания результатов броска была равна 2. Ни один из этих вариантов не имеет преимущества перед другим.
Cлайд 5
В таких ситуациях, когда варианты событий не имеют друг перед другом преимущества, говорят, что события эти равновероятные. Вероятность – это возможность того, что событие произойдёт. Неопределённость знания о некотором событии – это количество возможных равновероятных результатов события.
Cлайд 6
Сообщение о том, что произошло одно событие из двух равновероятных, несёт 1 бит информации. (Закодируем: «да» или «нет» - «1» или «0»; «орёл» или «решка» - «1» или «0»). 1 или 0
Cлайд 7
Примеры: Подбрасывание монеты («орёл» или «решка») – неопределённость знаний равна 2, т.к. есть всего два возможных результата бросания. Бросание игрального кубика - неопределённость знаний равна 6, т.к. кубик с шестью гранями может с равной вероятностью упасть на любую из них.
Cлайд 8
2i=N N – число равновероятных событий i – количество информации в сообщении
Cлайд 9
Не одинаковая вероятность Пример: В коробке имеется 50 шаров. Из них 40 белых и 10 чёрных. Вероятность того, что при вытаскивании «не глядя» попадётся белый шар больше, чем вероятность попадания чёрного. - вероятность попадания чёрного шара; - вероятность попадания белого шара.
Cлайд 10
Расчёт количества информации - вероятность события, где K - количество интересующих нас событий, N - общее число возможных исходов (событий) какого-то процесса. Количество информации или
Cлайд 11
В задаче о шарах определим количество информации в сообщении о попадании белого шара и чёрного шара:
Cлайд 12
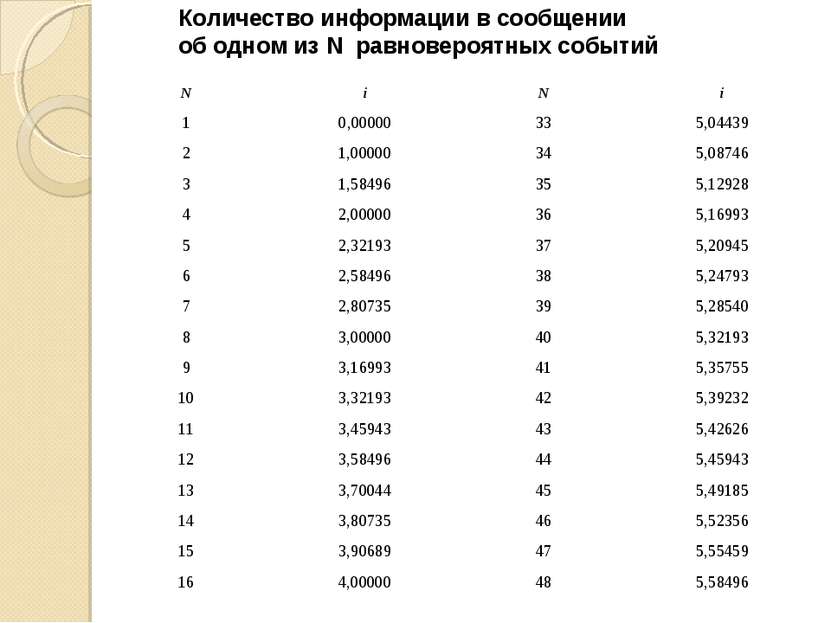
Количество информации в сообщении об одном из N равновероятных событий N i N i 1 0,00000 33 5,04439 2 1,00000 34 5,08746 3 1,58496 35 5,12928 4 2,00000 36 5,16993 5 2,32193 37 5,20945 6 2,58496 38 5,24793 7 2,80735 39 5,28540 8 3,00000 40 5,32193 9 3,16993 41 5,35755 10 3,32193 42 5,39232 11 3,45943 43 5,42626 12 3,58496 44 5,45943 13 3,70044 45 5,49185 14 3,80735 46 5,52356 15 3,90689 47 5,55459 16 4,00000 48 5,58496
Cлайд 13
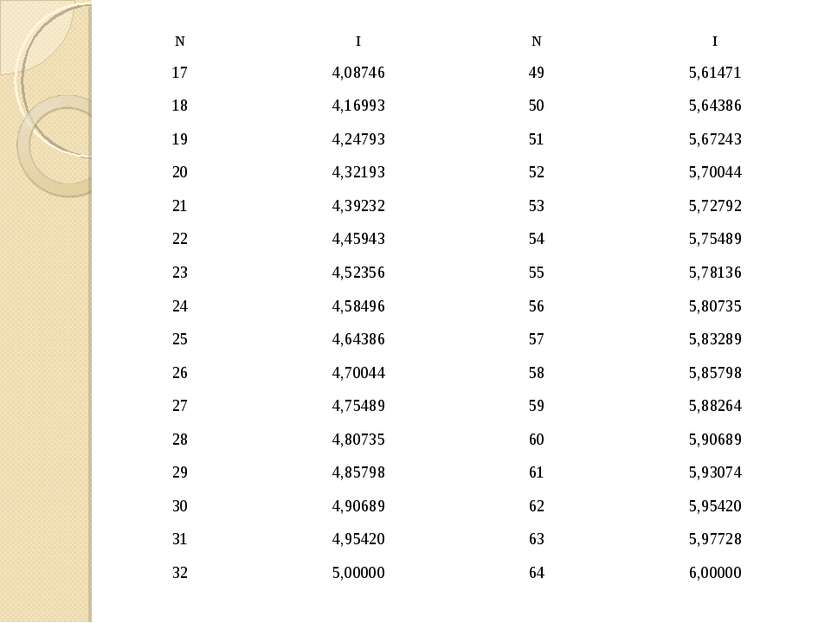
N I N I 17 4,08746 49 5,61471 18 4,16993 50 5,64386 19 4,24793 51 5,67243 20 4,32193 52 5,70044 21 4,39232 53 5,72792 22 4,45943 54 5,75489 23 4,52356 55 5,78136 24 4,58496 56 5,80735 25 4,64386 57 5,83289 26 4,70044 58 5,85798 27 4,75489 59 5,88264 28 4,80735 60 5,90689 29 4,85798 61 5,93074 30 4,90689 62 5,95420 31 4,95420 63 5,97728 32 5,00000 64 6,00000
Cлайд 14
Источники: 1. Задачник-практикум. Т.1. / Под редакцией И.Г. Семакина, Е.К. Хеннера, БИНОМ, 2004.
