X
Код презентации скопируйте его
Этот удивительный Мир симметрии
Скачать эту презентацию
Презентация на тему Этот удивительный Мир симметрии
Скачать эту презентациюCлайд 1
Этот удивительный Мир симметрии Работа: Гибадуллиной Карины, члена творческого объединения «Экос». Руководители: Миннигалеева А.Н., учитель биологии.
Cлайд 2
«Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство». Г. Вейль. «СИММЕТРИЯ - такое расположение частей предмета или организма, при котором по обе стороны срединной линии все части представляют полное и точное повторение». Брокгауз. «Быть прекрасным - значит быть симметричным и соразмерным». Платон. Симметрия
Cлайд 3
Цель работы: рассмотреть проявление симметрии в разных областях науки. Задачи работы: проведение анализа школьного материала; выявление упоминания материала о симметрии в различных областях науки ; развитие межпредметных связей в школьном курсе Цели и задачи
Cлайд 4
Симметрия в математике
Cлайд 5
Центральная симметрия. Две точки А и А1 называются симметричными относительно точки О, если О - середина отрезка АА1. Точка О считается симметричной самой себе.
Cлайд 6
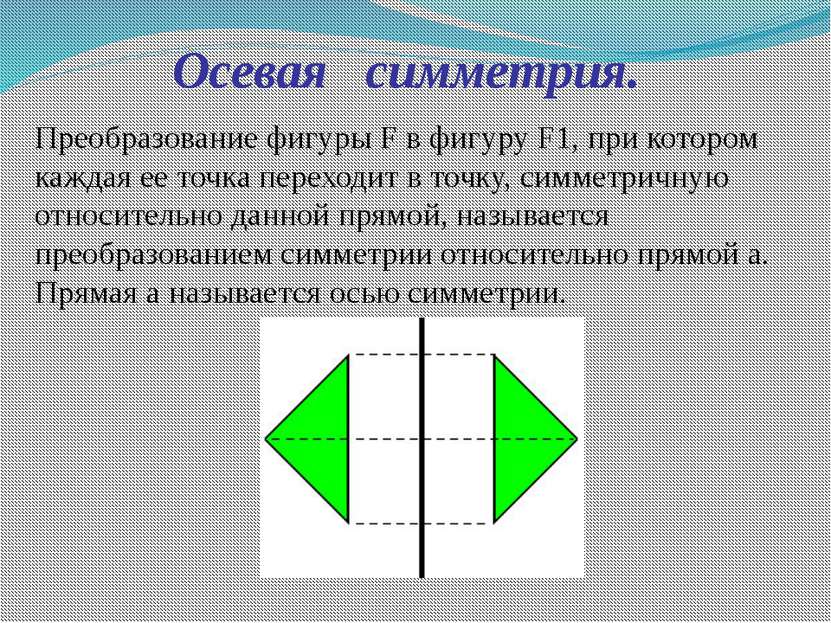
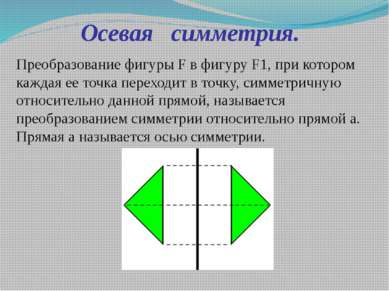Преобразование фигуры F в фигуру F1, при котором каждая ее точка переходит в точку, симметричную относительно данной прямой, называется преобразованием симметрии относительно прямой а. Прямая а называется осью симметрии. Осевая симметрия.
Cлайд 7
Зеркально-поворотная симметрия. Если во внутрь квадрата вписать с поворотом другой квадрат, то это и будет пример зеркально - поворотной симметрии.
Cлайд 8
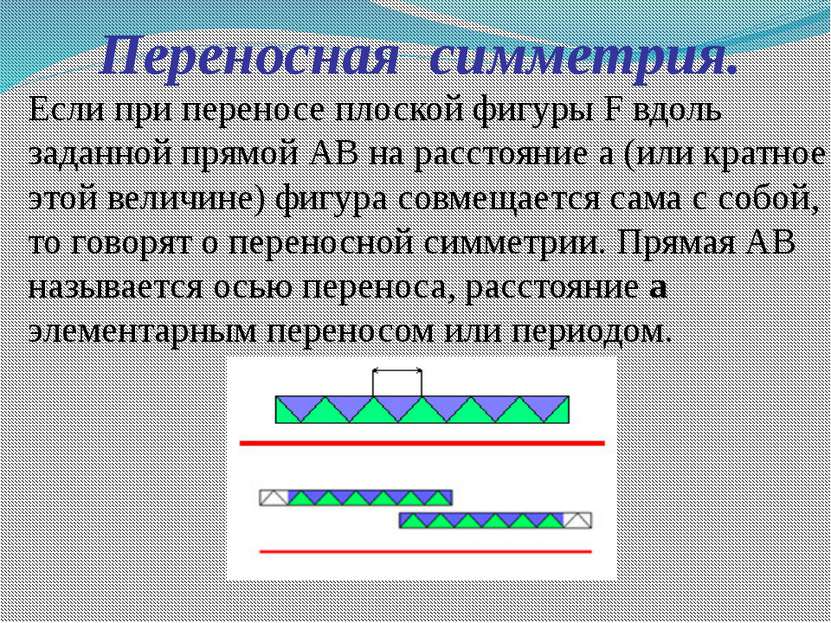
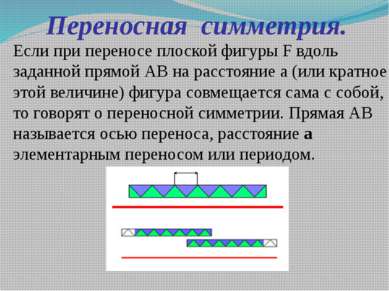Переносная симметрия. Если при переносе плоской фигуры F вдоль заданной прямой АВ на расстояние а (или кратное этой величине) фигура совмещается сама с собой, то говорят о переносной симметрии. Прямая АВ называется осью переноса, расстояние а элементарным переносом или периодом.
Cлайд 9
Симметрия в биологии
Cлайд 10
Симметрия у растений. Симметрия конуса Вертикальная плоскость симметрии.
Cлайд 11
Радиальная и билатеральная симметрия. Цветки, имея парные части, считаются цветками с двойной симметрией
Cлайд 12
Пятерная симметрия обычна для двудольных растений Тройная симметрия обычна для однодольных растений
Cлайд 13
Симметрия у животных
Cлайд 14
Радиальная или лучистая симметрия Билатеральная симметрия
Cлайд 15
Билатеральная симметрия
Cлайд 16
Симметрия у человека
Cлайд 17
Двусторонняя симметрия
Cлайд 18
Симметрия в ХИМИИ.
Cлайд 19
Молекула воды имеет плоскость симметрии - прямая вертикальная линия
Cлайд 20
Молекулы ДНК (дезоксирибонуклеиновая кислота)
Cлайд 21
Молекула метана СН4
Cлайд 22
Симметрия в ФИЗИКЕ.
Cлайд 23
Принцип относительности Галилея и Эйнштейна.
Cлайд 24
Симметрия электрического и магнитного поля
Cлайд 25
Симметричное распространение электромагнитных волн.
Cлайд 26
Конечное число типов кристаллов.
Cлайд 27
Симметрия в архитектуре
Cлайд 28
Cлайд 29
Заключение Симметрия! Я гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой башне, в малой мошке, Ты в ёлочке, что у лесной дорожки, С тобою в дружбе и тюльпан и роза, И снежный рой- творение мороза. Н.К.Антонович, г. Новосибирск
