X
Код презентации скопируйте его
Гипотеза пуанкаре и терстона
Скачать эту презентациюПрезентация на тему Гипотеза пуанкаре и терстона
Скачать эту презентациюCлайд 2
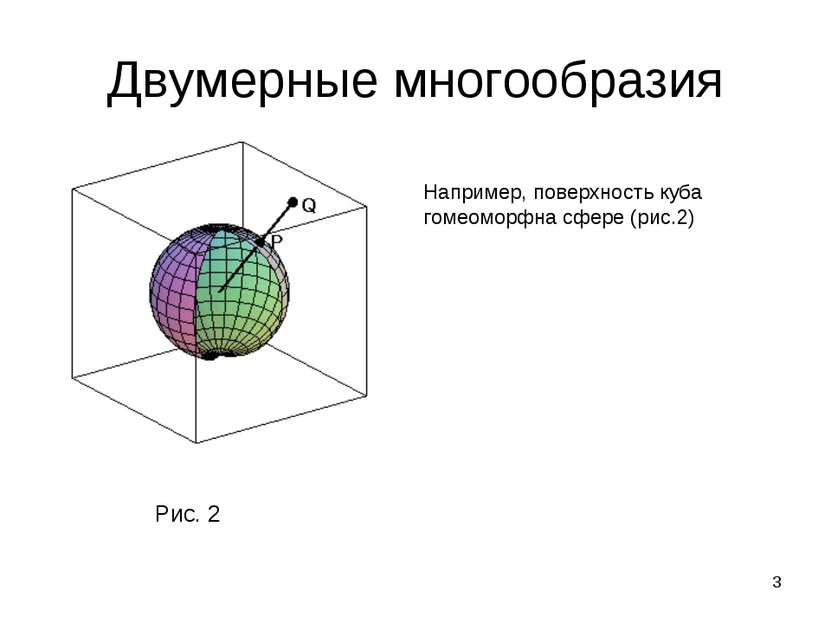
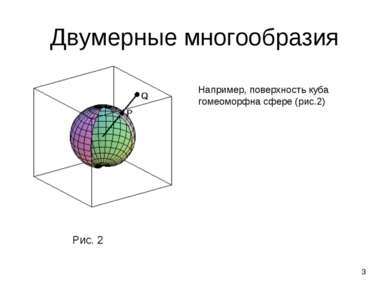
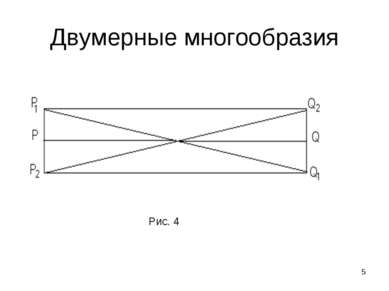
 * Двумерные многообразия Пусть и – два множества в евклидовом пространстве произвольной размерности. Если задано отображение , которое каждой точке множества ставит в соответствие точку множества и 1) отображение взаимно-однозначно, то есть различные точки переходят в различные; 2) отображение непрерывно, то есть близкие точки переходят в близкие; 3) обратное отображение непрерывно, то множества и – гомеоморфны, а отображение называется гомеоморфизмом. Рис. 1 Например, внутренность круга гомеоморфна всей плоскости (рис.1)
* Двумерные многообразия Пусть и – два множества в евклидовом пространстве произвольной размерности. Если задано отображение , которое каждой точке множества ставит в соответствие точку множества и 1) отображение взаимно-однозначно, то есть различные точки переходят в различные; 2) отображение непрерывно, то есть близкие точки переходят в близкие; 3) обратное отображение непрерывно, то множества и – гомеоморфны, а отображение называется гомеоморфизмом. Рис. 1 Например, внутренность круга гомеоморфна всей плоскости (рис.1)
Cлайд 7
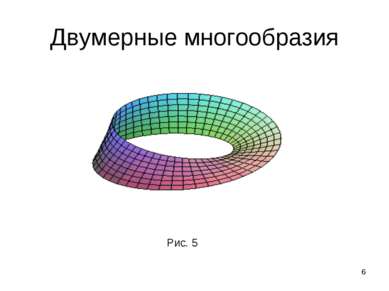
 * Двумерные многообразия Любая компактная двумерная поверхность гомеоморфна либо сфере с p ручками, либо сфере с q листами Мебиуса, причем сферы с ручками не гомеоморфны сферам с листами Мебиуса, так как второй ряд поверхностей образуют неориенти-руемые поверхности. Сферы с различным числом ручек и различным числом листов Мебиуса также негомеоморфны между собой. Рис. 6
* Двумерные многообразия Любая компактная двумерная поверхность гомеоморфна либо сфере с p ручками, либо сфере с q листами Мебиуса, причем сферы с ручками не гомеоморфны сферам с листами Мебиуса, так как второй ряд поверхностей образуют неориенти-руемые поверхности. Сферы с различным числом ручек и различным числом листов Мебиуса также негомеоморфны между собой. Рис. 6
Cлайд 12
 * Фундаментальная группа Рис. 11 Две петли и , проходящие через фиксированную точку P , называются гомотопными, если их можно непрерывно деформировать одна в другую. И мы уже можем рассматривать класс гомотопных петель.
* Фундаментальная группа Рис. 11 Две петли и , проходящие через фиксированную точку P , называются гомотопными, если их можно непрерывно деформировать одна в другую. И мы уже можем рассматривать класс гомотопных петель.
Cлайд 15
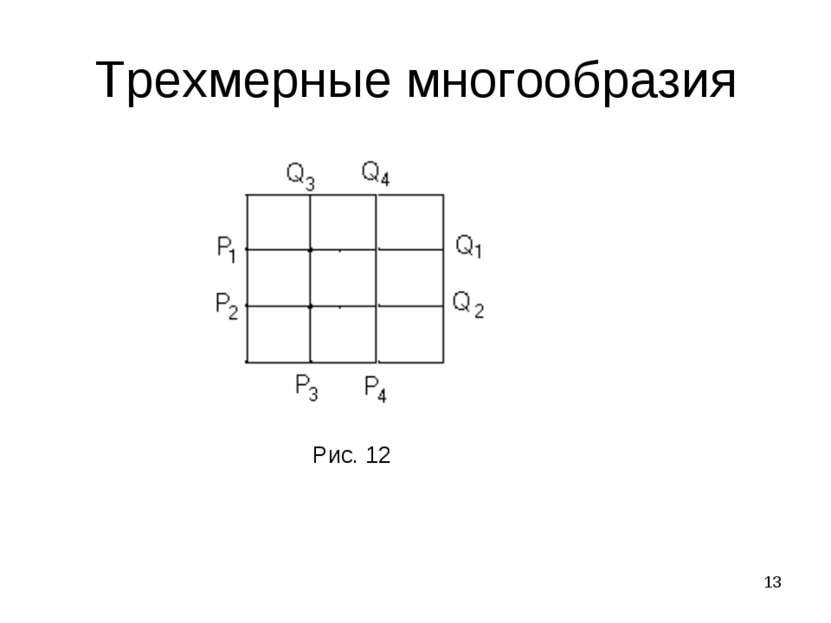
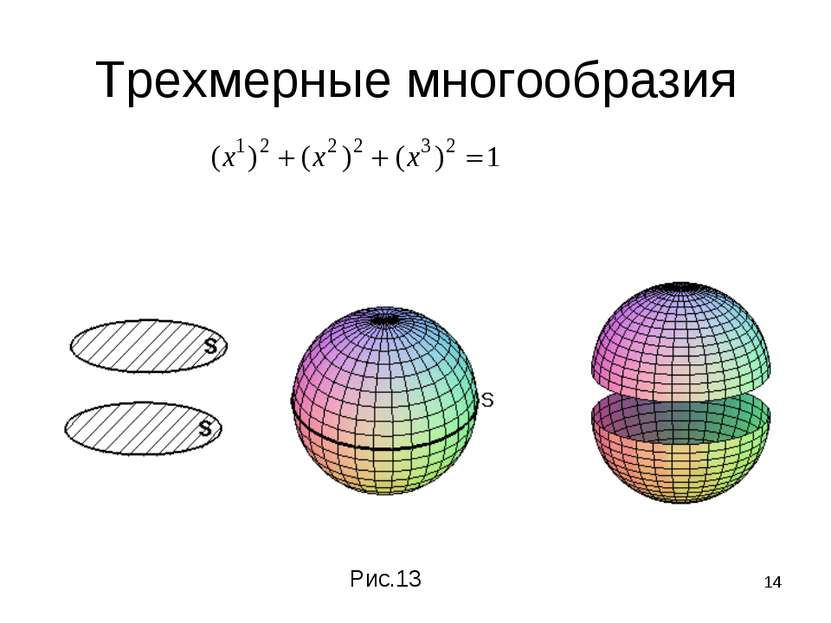
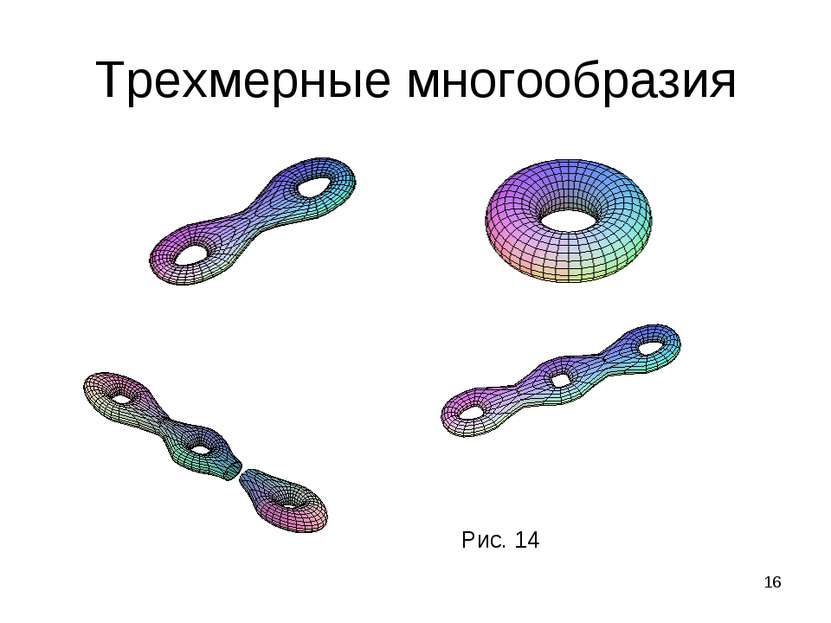
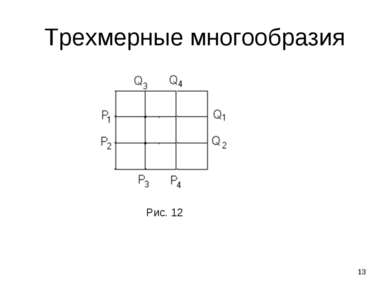
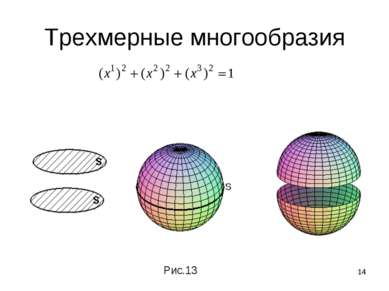
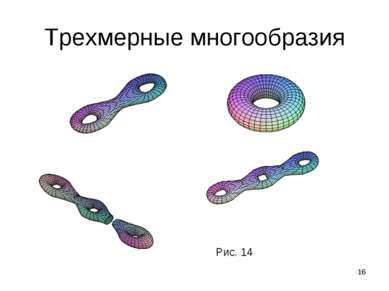
 * Трехмерные многообразия Каждое компактное ориентируемое 3-мерное многообразие раскладывается в связную сумму где сомножители - замкнутые неприводимые трехмерные многообразия, -декартово произведение окружности на двумерную сферу и в связную сумму входит r –компонент. множители имеют бесконечную фундаментальную группу, множители - конечную фундаментальную группу.
* Трехмерные многообразия Каждое компактное ориентируемое 3-мерное многообразие раскладывается в связную сумму где сомножители - замкнутые неприводимые трехмерные многообразия, -декартово произведение окружности на двумерную сферу и в связную сумму входит r –компонент. множители имеют бесконечную фундаментальную группу, множители - конечную фундаментальную группу.
Cлайд 17
 * Трехмерные многообразия Любое трехмерное компактное неприводимое многообразие можно разрезать конечным числом несжимающихся торов на компактные многообразия, границей которых есть торы.Каж-дое из этих многообразий или торонеприводимо или является многообразием Зейферта. Гипотеза Пуанкаре состоит в следующем. Пусть – ком-пактное трехмерное односвязное многообразие (т.е. любая петля на многообразии стягивается в точку). Верно ли, что это многообразие гомеоморфно трехмерной сфере ?
* Трехмерные многообразия Любое трехмерное компактное неприводимое многообразие можно разрезать конечным числом несжимающихся торов на компактные многообразия, границей которых есть торы.Каж-дое из этих многообразий или торонеприводимо или является многообразием Зейферта. Гипотеза Пуанкаре состоит в следующем. Пусть – ком-пактное трехмерное односвязное многообразие (т.е. любая петля на многообразии стягивается в точку). Верно ли, что это многообразие гомеоморфно трехмерной сфере ?
Cлайд 18
 * Однородные трехмерные геометрии В трехмерном случае всего 8 стандартных геометрий, которые 1) в окрестности каждой точки выглядят одинаково, пространство является однородным; 2) задаются на односвязном многообразии; 3) и для каждой геометрии существует трехмерное компактное многообразие, на котором она задается. Существование только 8 геометрий приписывается Терстону, но это следует из результатов Бианки. Перечислим их: 1) – метрика стандартной единичной сферы в ; 2) – евклидово пространство; 3) – трехмерное пространство Лобачевского;
* Однородные трехмерные геометрии В трехмерном случае всего 8 стандартных геометрий, которые 1) в окрестности каждой точки выглядят одинаково, пространство является однородным; 2) задаются на односвязном многообразии; 3) и для каждой геометрии существует трехмерное компактное многообразие, на котором она задается. Существование только 8 геометрий приписывается Терстону, но это следует из результатов Бианки. Перечислим их: 1) – метрика стандартной единичной сферы в ; 2) – евклидово пространство; 3) – трехмерное пространство Лобачевского;
Cлайд 19
 * Однородные трехмерные геометрии Метрики прямого произведения: 4) ; 5) ; Возьмем пространство единичных окружностей в касательных пространствах к плоскости Лобачевского . В нем вводится естественная метрика Сасаки. Универсальное накрывающее пространство и есть 6) ; 7) Nil ; Это трехмерная группа Гейзенберга, состоящая из матриц ,
* Однородные трехмерные геометрии Метрики прямого произведения: 4) ; 5) ; Возьмем пространство единичных окружностей в касательных пространствах к плоскости Лобачевского . В нем вводится естественная метрика Сасаки. Универсальное накрывающее пространство и есть 6) ; 7) Nil ; Это трехмерная группа Гейзенберга, состоящая из матриц ,
Cлайд 20
 * Однородные трехмерные геометрии которые образуют группу относительно операции умножения и на ней задана метрика Sol . Это трехмерная группа, на которой задана метрика . Заметим, что только сфера является односвязным компактным многообразием, на котором задана стандартная геометрия.
* Однородные трехмерные геометрии которые образуют группу относительно операции умножения и на ней задана метрика Sol . Это трехмерная группа, на которой задана метрика . Заметим, что только сфера является односвязным компактным многообразием, на котором задана стандартная геометрия.
Cлайд 21
 * Геометрическая гипотеза Терстона Неприводимое трехмерное замкнутое многообразие разрезается несжимающимися торами на куски, на которых можно задать одну из стандартных геометрий.
* Геометрическая гипотеза Терстона Неприводимое трехмерное замкнутое многообразие разрезается несжимающимися торами на куски, на которых можно задать одну из стандартных геометрий.