X
Код презентации скопируйте его
Амидекстр
Скачать эту презентацию
Презентация на тему Амидекстр
Скачать эту презентациюCлайд 1
Прямоугольный параллелепипед. Работу выполнила Ученица 5 «В» класса Мендыгалиева Алина МОУ «Гимназия» №6
Cлайд 2
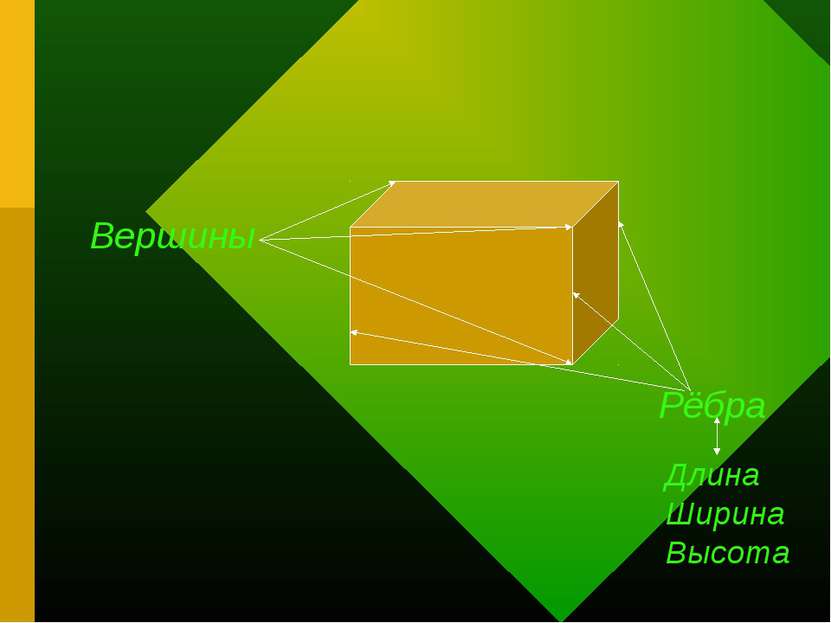
Параллелепипед Параллелепипед – шестигранник, все грани которого (основания) – параллелограммы. Параллелепипед имеет 8 вершин и 12 рёбер. Грани параллелепипеда, не имеющие общих вершин, называются противоположными.
Cлайд 3
Вершины Рёбра Длина Ширина Высота
Cлайд 4
Параллелепипед Они равны и лежат в параллельных плоскостях. Диагонали параллелепипеда, то есть отрезки, соединяющие вершины параллелепипеда, не принадлежащие какой – либо одной грани, пересекаются в одной точке и делятся ею по полам.
Cлайд 5
Параллелепипед Параллелепипед называется прямым или прямоугольным, если все его грани – прямоугольники; это - прямая четырёхугольная призма. Параллелепипед, все грани которого квадраты, называется кубом.
Cлайд 6
Параллелепипед Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называются его измерениями. Квадрат длинны диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Cлайд 7
Параллелепипед Объём параллелепипеда равен произведению площади основания (какой – либо его грани) на высоту (расстояние между основанием и противоположной гранью). Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
Cлайд 8
Параллелепипед Название «параллелепипед» происходит от греческого слова «параллелос», означающего «параллельный», и греческого слова «эпипедос», означающего «плоскость», «поверхность». Слово встречалось у древнегреческих ученых Евклида и Герона.
Cлайд 9
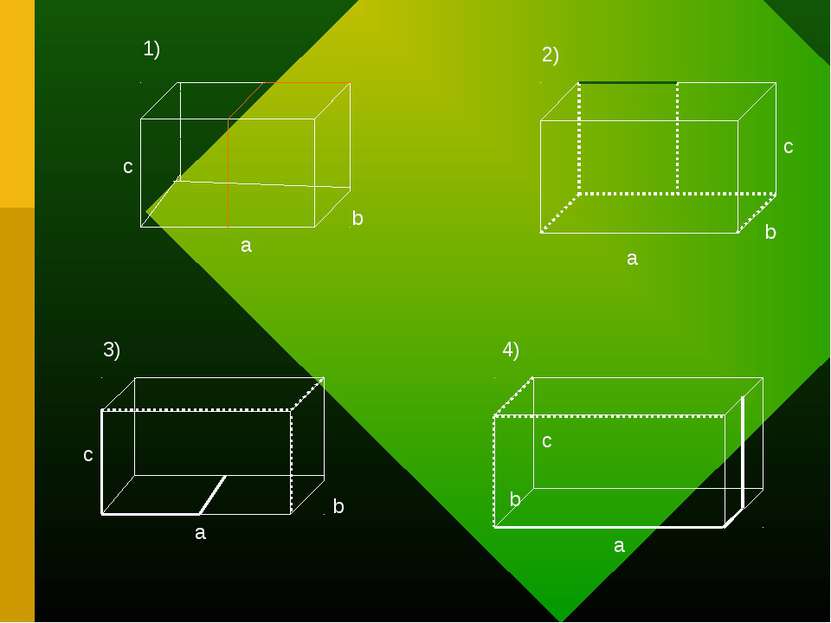
Объём прямоугольного параллелепипеда. Найди объём V1 прямоугольного параллелепипеда с размерами a, b и c, сумму Р длин всех его рёбер и длину l жирной линии, у которой концы и точки перегиба – вершины параллелепипеда или середины его рёбер. Найди объём V2 параллелепипеда с размерами в два раза меньше.
Cлайд 10
Представь положение жирной линии в пространстве и согни её из проволоки.
Cлайд 11
1) с а b 2) b а с 3) а b с b а с 4)
Cлайд 12
a b c V1 V2 P l 1 2,4 1,6 0,8 2 3,2 2,8 0,6 3 1,4 3,6 2,2 4 2,6 1,2 1,6
Cлайд 13
