X
Код презентации скопируйте его
Признаки равенства и подобия треугольников
Скачать эту презентацию
Презентация на тему Признаки равенства и подобия треугольников
Скачать эту презентациюCлайд 1
О равенстве треугольников О подобии треугольников Признаки равенства и подобия треугольников Оглавление EXIT
Cлайд 2
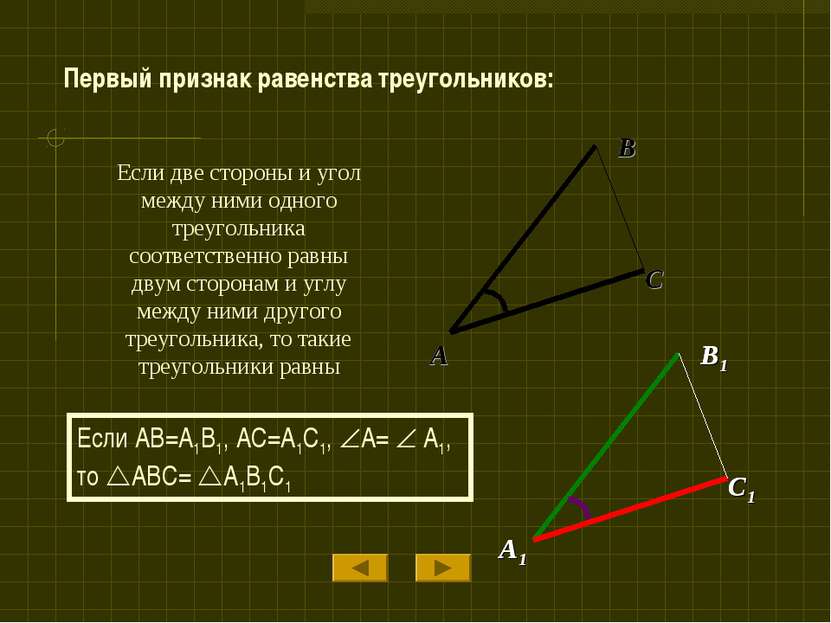
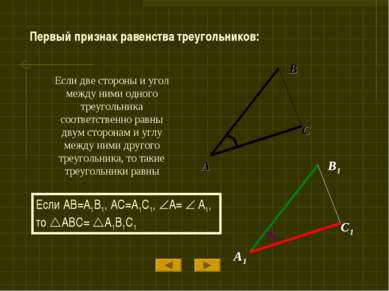Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны Если AB=A1B1, AC=A1C1, A= A1, то ABC= A1B1C1 Первый признак равенства треугольников:
Cлайд 3
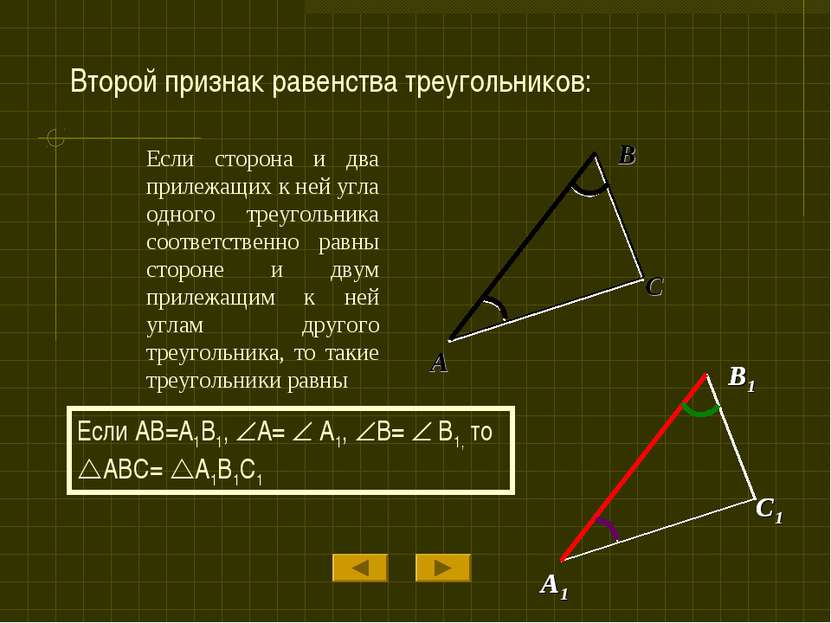
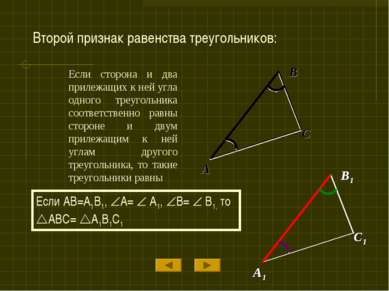Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны Если AB=A1B1, A= A1, B= B1, то ABC= A1B1C1 Второй признак равенства треугольников: A1 B1 C1 B C A
Cлайд 4
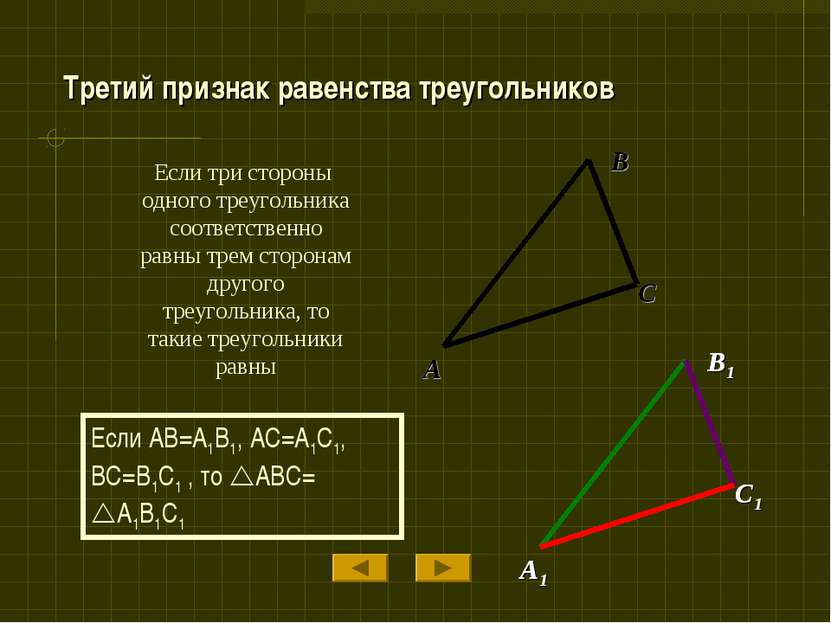
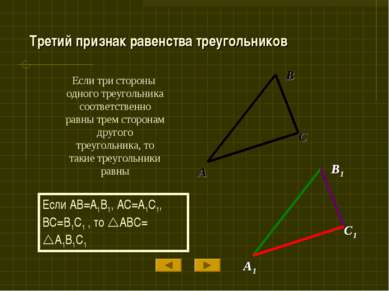Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны B A C Если AB=A1B1, AC=A1C1, BC=B1C1 , то ABC= A1B1C1 Третий признак равенства треугольников B1 A1 C1
Cлайд 5
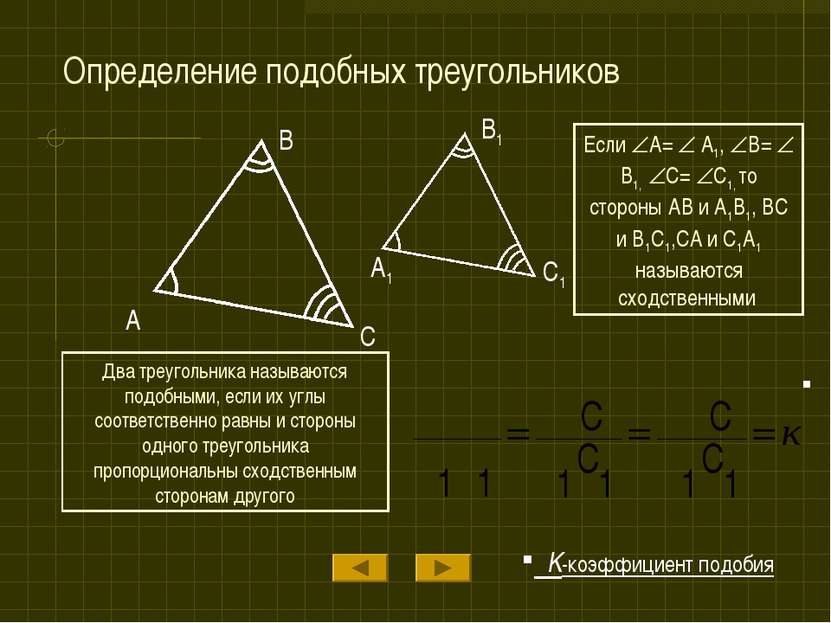
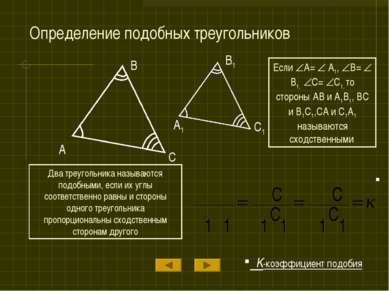Определение подобных треугольников A B C A1 B1 C1 Если A= A1, B= B1, C= C1, то стороны AB и A1B1, BC и B1C1,CA и C1A1 называются сходственными Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого K-коэффициент подобия
Cлайд 6
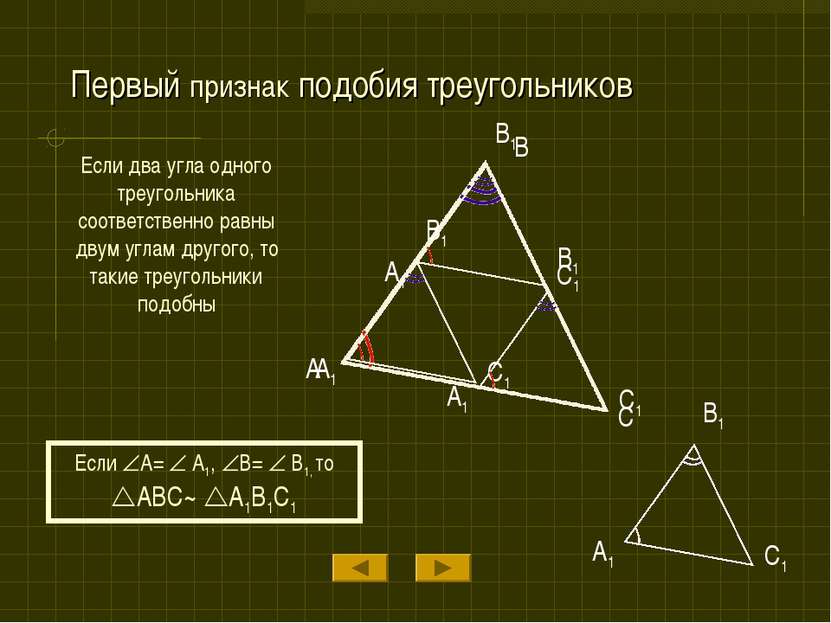
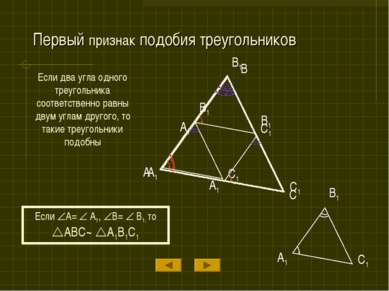Первый признак подобия треугольников Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны A B C A1 B1 C1 Если A= A1, B= B1, то ABC~ A1B1C1
Cлайд 7
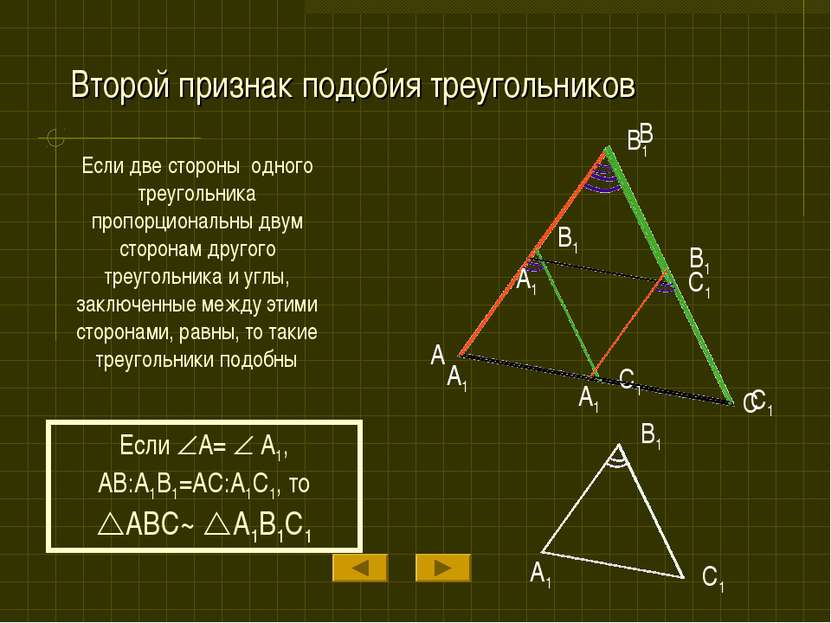
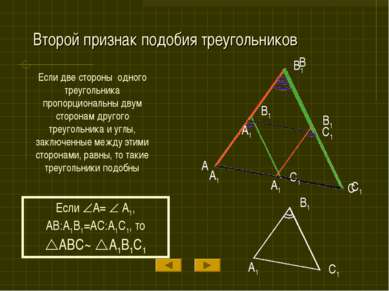Второй признак подобия треугольников Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны A B C Если A= A1, AB:A1B1=AC:A1C1, то ABC~ A1B1C1
Cлайд 8
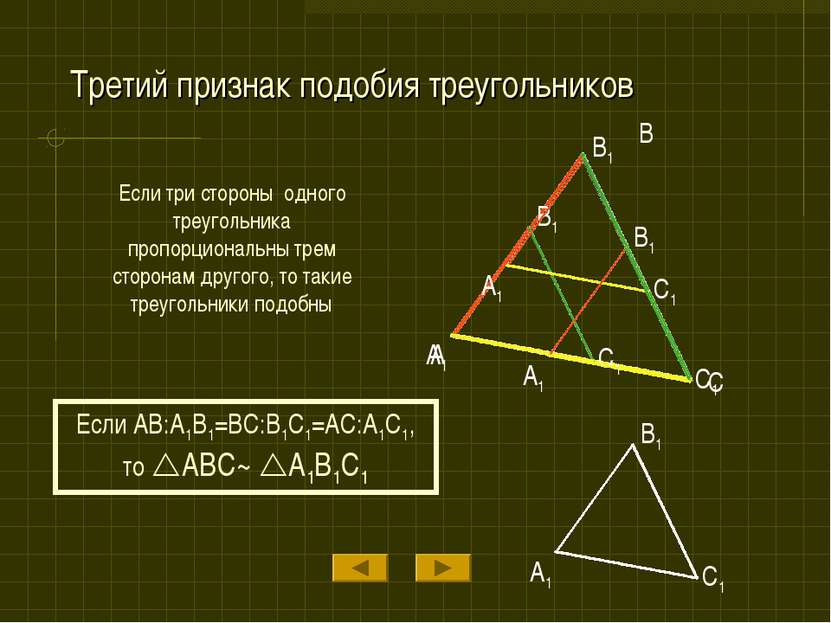
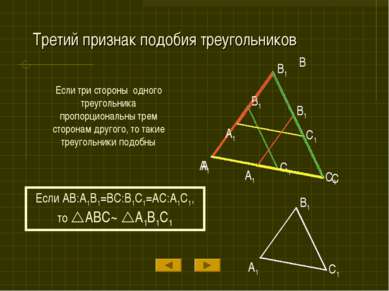Третий признак подобия треугольников Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны Если AB:A1B1=BC:B1C1=AC:A1C1, то ABC~ A1B1C1
Cлайд 9
Задачи На равенство треугольников ОТВЕТЫ На подобие треугольников
Cлайд 10
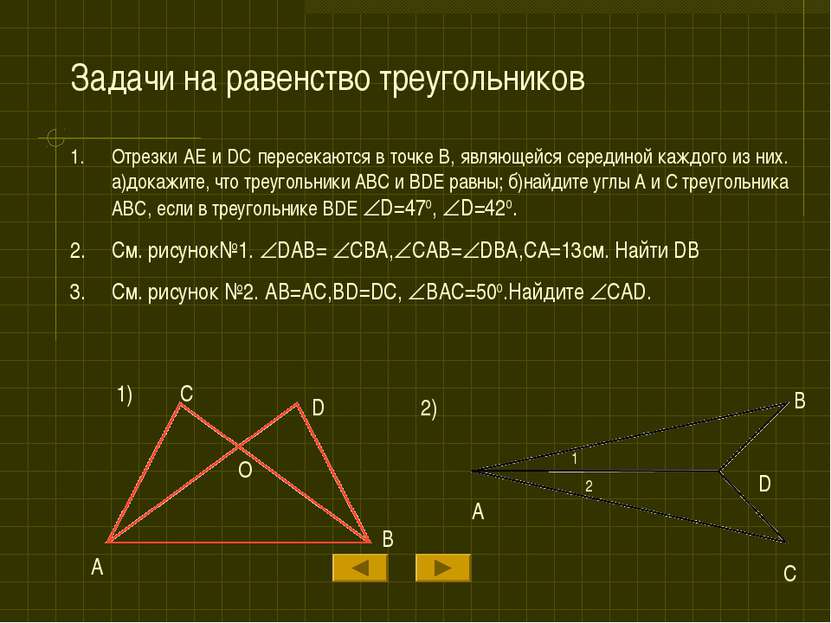
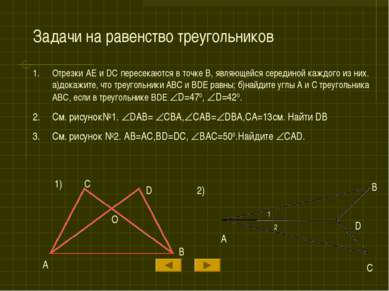Задачи на равенство треугольников Отрезки AE и DC пересекаются в точке B, являющейся серединой каждого из них. а)докажите, что треугольники ABC и BDE равны; б)найдите углы A и C треугольника ABC, если в треугольнике BDE D=470, D=420. См. рисунок№1. DAB= CBA, CAB= DBA,CA=13см. Найти DB См. рисунок №2. AB=AC,BD=DC, BAC=500.Найдите CAD. 1) C A O D B 2) A B C D 1 2
Cлайд 11
Задачи на подобие треугольников Диагонали трапеции ABCD с основаниями AB и CD пересекаются в точке О. Найдите AB, если OB=4 см, OD=10 см, DC=25 см. Основания трапеции равны 5см и 8 см. Боковые стороны, продолжены до пересечения в точке M. Найдите расстояние от точки M до концов меньшего основания. Точки M,N,P лежат соответственно на сторонах AB,BC,CA треугольника ABC, причем MN ‖ AC, NP ‖ AB. Найдите стороны четырехугольника AMNP, если AB=10 см, AC=15 см, PN:MN=2:3.
Cлайд 12
Ответы Задачи на равенство треугольников б)420,470 13 см 250 Задачи на подобие треугольников 10 см 6 см и 6,5 см 5 см;5 см;7.5 см;7.5 см
Cлайд 13
Оглавление: Признаки равенства и подобия треугольников Равенство: Первый признак равенства треугольников Второй признак равенства треугольников Третий признак равенства треугольников Подобие: Определение подобных треугольников Первый признак подобия треугольников Второй признак подобия треугольников Третий признак подобия треугольников 4. Задачи на равенство 5. Задачи на подобие 6. Ответы
Cлайд 14
О программе Учебник включает в себя определения и признаки равенства и подобия треугольников, задачи на эти темы и ответы к ним. Страницы учебника можно перелистывать подряд, как книгу или выбрать интересующую Вас тему и работать только с ней. Я надеюсь, что моя презентация окажется полезной. Хотя бы чуть - чуть. Спасибо за то, что вы ее хотя бы посмотрели! (а если чему-то научились — шоколадка за вами) Экзаменационный проект по информатике (оценка пока неизвестна) Шакировой Саиды, ученицы 11 «Б» класса МОУ «Лицей» с. Ельники Руководитель Побожьев С.К. Shakiroff EXIT
