X
Код презентации скопируйте его
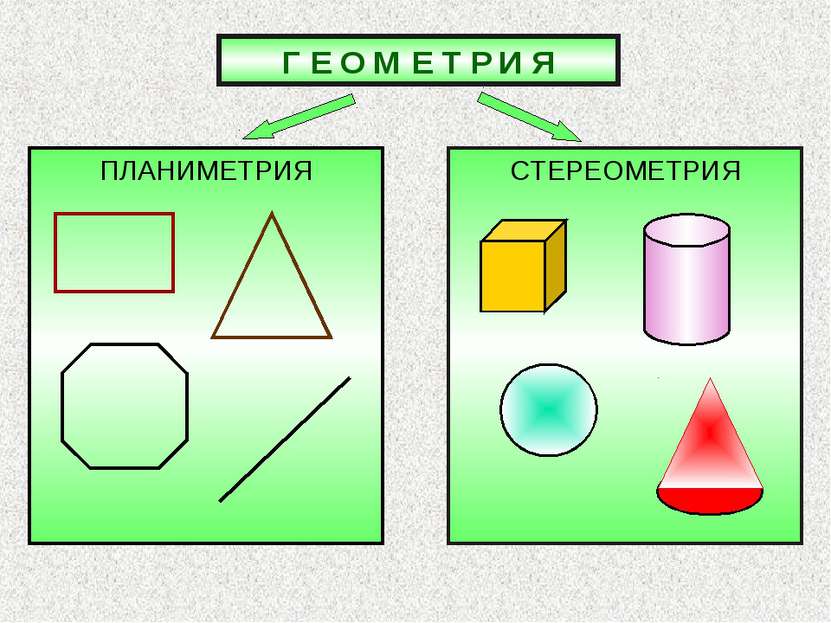
Что изучает геометрия 7 класс
Скачать эту презентацию
Презентация на тему Что изучает геометрия 7 класс
Скачать эту презентациюCлайд 1
Урок геометрии 7 класс Учитель Мухина Людмила Петровна
Cлайд 2
Cлайд 3
Cлайд 4
Геология – наука о составе, строении и истории Земли и земной коры Геодезия – наука об определении формы и размеров Земли Геоботаника – наука о растительном покрове Земли Геоакустика – наука о распространении упругих волн в земной коре
Cлайд 5
ГЕО - Земля МЕТРЕО – измеряю ИЗМЕРЕНИЕ ЗЕМЛИ или ЗЕМЛЕМЕРИЕ
Cлайд 6
ГЕОМЕТРИЯ – древняя математическая наука Место рождения - Древний Египет
Cлайд 7
Древняя Греция (VII-V вв.до н.э.) Древнегреческий философ Платон Евклид «НАЧАЛА» Александрия (около 300 г. до н.э.)
Cлайд 8
Получил традиционное для аристократического юноши хорошее воспитание (физическое и мусическое). В юности слушал софиста гераклитовской ориентации Кратила, в 20 лет познакомился с Сократом, начал регулярно посещать его беседы и отказался от реальной политической карьеры. Отличался крайней застенчивостью и замкнутостью. После смерти Сократа (399) Платон уезжает в Мегары. Принимает участие в Коринфской войне, в походах в Танагру (395) и Коринф (394). В 387 посещает Южную Италию, Локры Эпизефирские — родину древнейших записанных законов Залевка (из Локр происходит пифагореец Тимей, именем которого назван знаменитый диалог Платона, путешествие вообще задумывалось прежде всего ради знакомства с пифагорейцами). В Сицилии (Сиракуза), он знакомится с Дионом, приближенным правителя Сиракуз Дионисия I Старшего. По возвращении из Сицилии (387) основал в Афинах свою философскую школу — в гимнасии Академия. Знакомство с Дионом, попавшим под обаяние личности Платона и его образа мыслей, способствовало тому, что в 367-366 и 361 Платон совершил еще две поездки в Сицилию. ПЛАТОН (428 или 427 до н. э. — 348 или 347), древнегреческий философ. Ученик Сократа, ок. 387 основал в Афинах школу. Происходил из аристократической семьи, принимавшей активное участие в политической жизни Афин (род его отца Аристона, по преданию, восходил к мифическому царю Кодру; среди предков матери, Периктионы, — законодатель Солон; после победы спартанцев в Пелопоннесской войне дядя Платона, Хармид, — один из Десяти ставленников Лисандра в Пирее в 404-403, Критий — один из Тридцати тиранов в Афинах).
Cлайд 9
Сведения о времени и месте его рождения до нас не дошли, однако известно, что Евклид жил в Александрии и расцвет его деятельности приходится на время царствования в Египте Птолемея I Сотера. Известно также, что Евклид был моложе учеников Платона (427—347 до н. э.), но старше Архимеда (ок. 287—212 до н. э.), так как, с одной стороны, был платоником и хорошо знал философию Платона (именно поэтому он закончил «Начала» изложением т. н. платоновых тел, т. е. пяти правильных многогранников), а с другой стороны — его имя упоминается в первом из двух писем Архимеда к Досифею «О шаре и цилиндре». С именем Евклида связывают становление александрийской математики (геометрической алгебры) как науки. Из дошедших до нас сочинений Евклида наиболее знамениты «Начала», состоящие из 15 книг. В 1-й книге формулируются исходные положения геометрии, а также содержатся основополагающие теоремы планиметрии, среди которых теорема о сумме углов треугольника и теорема Пифагора. Во 2-й книге излагаются основы геометрической алгебры. 3-я книга посвящена свойствам круга, его касательных и хорд. В 4-й книге рассматриваются правильные многоугольники, причем построение правильного пятнадцатиугольника принадлежит, видимо, самому Евклиду. Книга 5-я и 6-я посвящены теории отношений и ее применению к решению алгебраических задач. Книга 7-я, 8-я и 9-я посвящены теории целых и рациональных чисел, разработанной пифагорейцами не позднее 5 в. до н. э. ЕВКЛИД (умер между 275 и 270 до н. э.), древнегреческий математик. Работал в Александрии в 3 в. до н. э. Главный труд «Начала» (15 книг), содержащий основы античной математики, элементарной геометрии, теории чисел, общей теории отношений и метода определения площадей и объемов, включавшего элементы теории пределов, оказал огромное влияние на развитие математики. Работы по астрономии, оптике, теории музыки.
Cлайд 10
ГЕОМЕТРИЯ - наука, занимающаяся изучением геометрических фигур
Cлайд 11
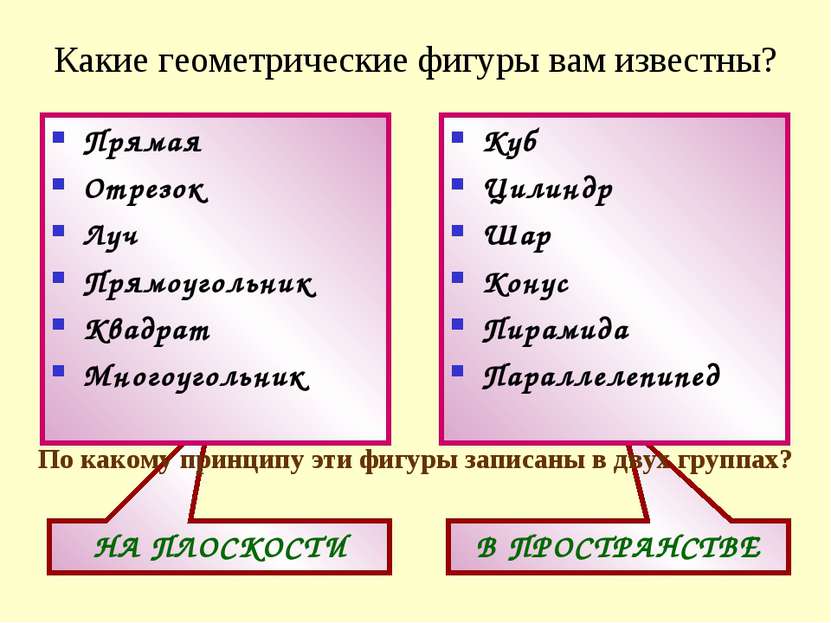
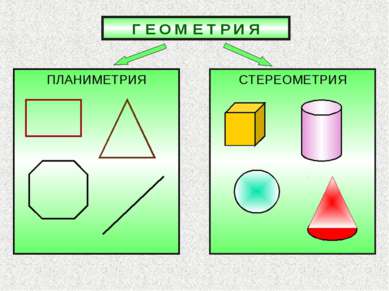
В ПРОСТРАНСТВЕ НА ПЛОСКОСТИ Какие геометрические фигуры вам известны? Прямая Отрезок Луч Прямоугольник Квадрат Многоугольник Куб Цилиндр Шар Конус Пирамида Параллелепипед По какому принципу эти фигуры записаны в двух группах?
Cлайд 12
Г Е О М Е Т Р И Я ПЛАНИМЕТРИЯ СТЕРЕОМЕТРИЯ
Cлайд 13
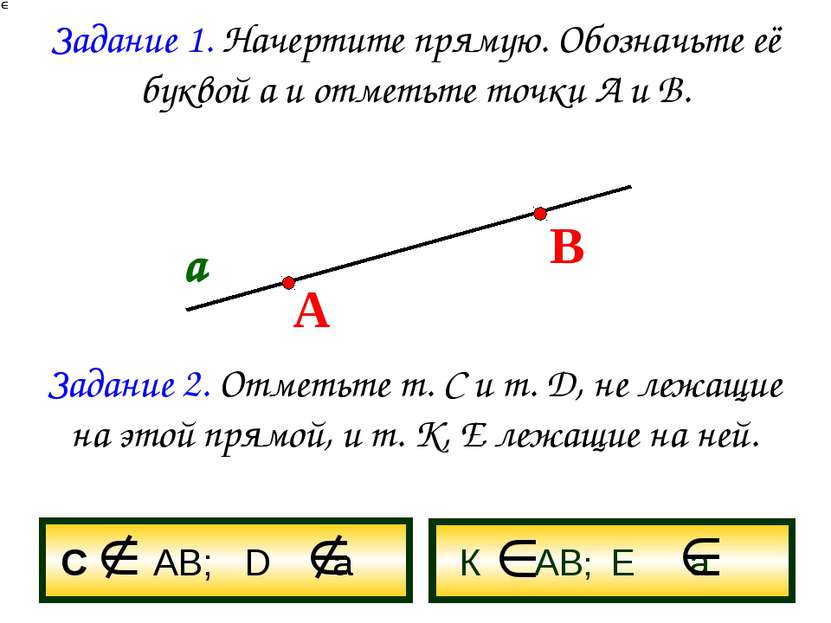
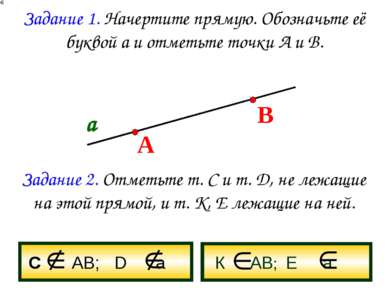Задание 1. Начертите прямую. Обозначьте её буквой а и отметьте точки А и В. а А В Задание 2. Отметьте т. С и т. D, не лежащие на этой прямой, и т. К, Е лежащие на ней. С АВ; D а К АВ; Е а
Cлайд 14
Задание 3. Сколько прямых можно провести через заданную точку А? Чертёж1 Задание 4. Сколько прямых можно провести через две точки? Чертёж2
Cлайд 15
Задание 5. Начертите прямые MN и КР , пересекающиеся в т.О М N К Р О
Cлайд 16
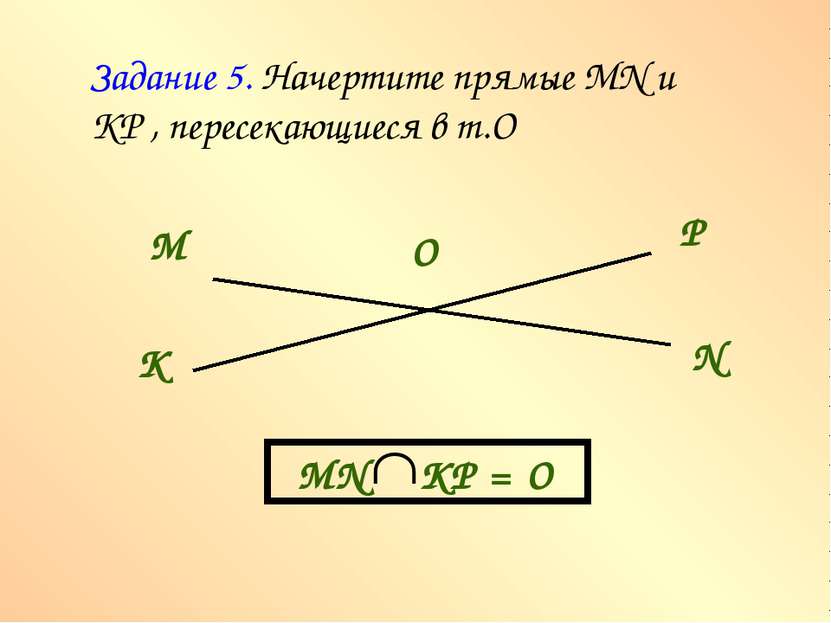
Задание 6. На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Чертёж 3 Чертёж 4
Cлайд 17
Задание 7. Сколько точек пересечения могут иметь три прямые?
Cлайд 18
3. Сколько прямых можно провести через две точки? одну две много 4. Сколько общих точек могут иметь две прямые? одну две много 1. Что означает слово «геометрия»? измерение землемерие теломерие 5. Какое наибольшее число прямых можно провести через различные пары из трёх точек? три шесть много 2. Сколько прямых можно провести через одну точку? одну две много
Cлайд 19
Домашнее задание: § 1, 2 Задачи 1, 3, 4, 7
