X
Код презентации скопируйте его
Решение прямоугольных треугольников
Скачать эту презентацию
Презентация на тему Решение прямоугольных треугольников
Скачать эту презентациюCлайд 1
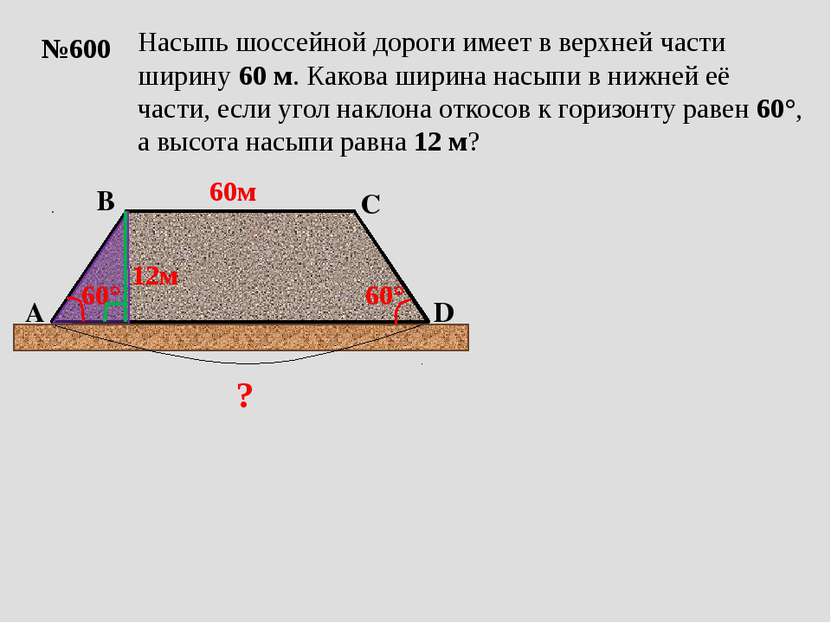
Решение прямоугольных треугольников Решение типовых задач Учебник «Геометрия 7-9» Л.В. Атанасян Урок геометрии в 8 классе Учитель математики высшей квалификационной категории МБОУО гимназия №36 г. Иваново Бычкова Оксана Владимировна
Cлайд 2
b α ? 1 α=38°; b=4 sinα cosα tgα 1 A C B
Cлайд 3
1 a α ? 2 α=27°; a=6 sinα cosα tgα 1 A C B
Cлайд 4
1 c α ? 3 α=54°; с=2 sinα cosα tgα 1 A C B
Cлайд 5
с α ? 4 α=77°; с=1 sinα cosα tgα 1 A C B
Cлайд 6
b α ? 5 α=25°; b=10 sinα cosα tgα 1 A C B
Cлайд 7
a α ? 6 α=32°; a=4 sinα cosα tgα 1 A C B
Cлайд 8
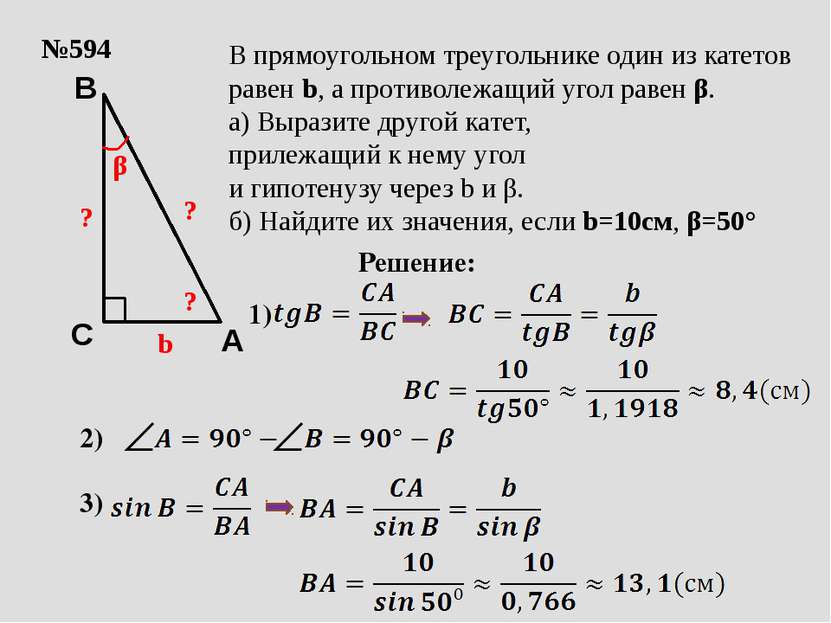
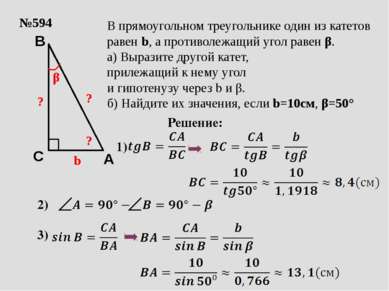№594 b β ? В прямоугольном треугольнике один из катетов равен b, а противолежащий угол равен β. а) Выразите другой катет, прилежащий к нему угол и гипотенузу через b и β. б) Найдите их значения, если b=10см, β=50° Решение: ? 1) 2) 3) ? A C B
Cлайд 9
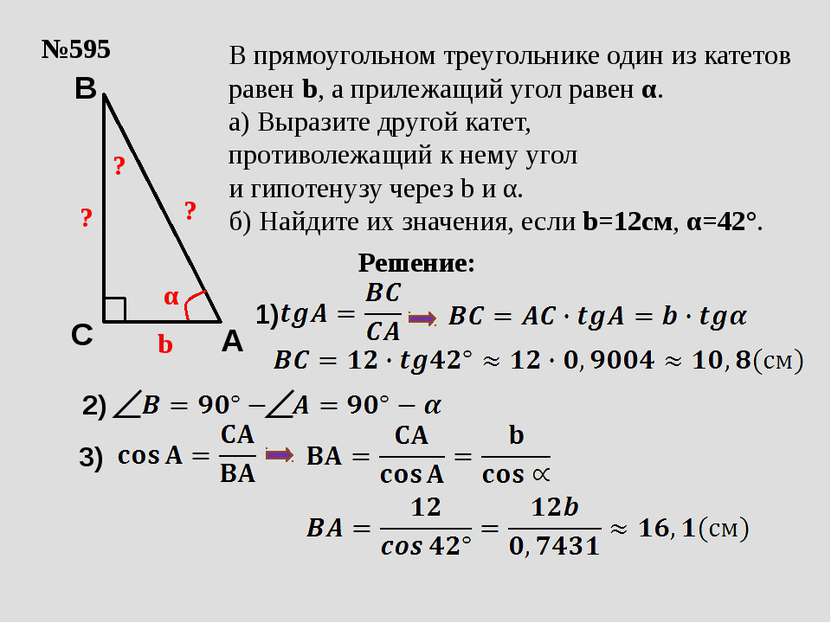
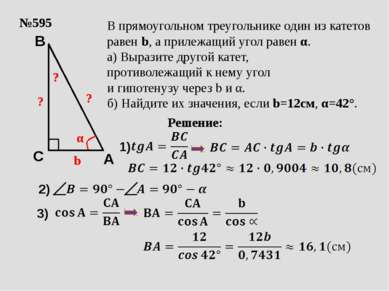№595 b α ? В прямоугольном треугольнике один из катетов равен b, а прилежащий угол равен α. а) Выразите другой катет, противолежащий к нему угол и гипотенузу через b и α. б) Найдите их значения, если b=12см, α=42°. Решение: ? ? A C B 1) 3) 2)
Cлайд 10
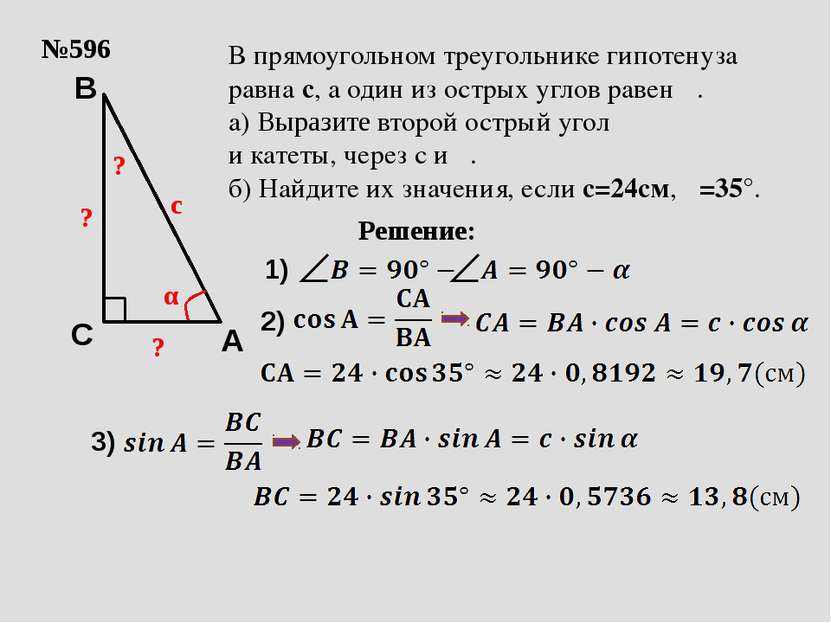
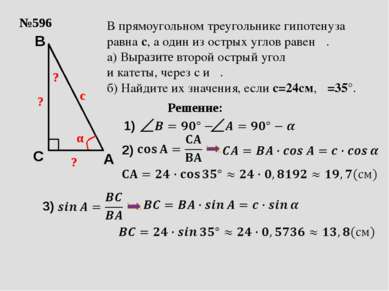№596 с α ? В прямоугольном треугольнике гипотенуза равна с, а один из острых углов равен α. а) Выразите второй острый угол и катеты, через с и α. б) Найдите их значения, если с=24см, α=35°. Решение: ? ? A C B 2) 3) 1)
Cлайд 11
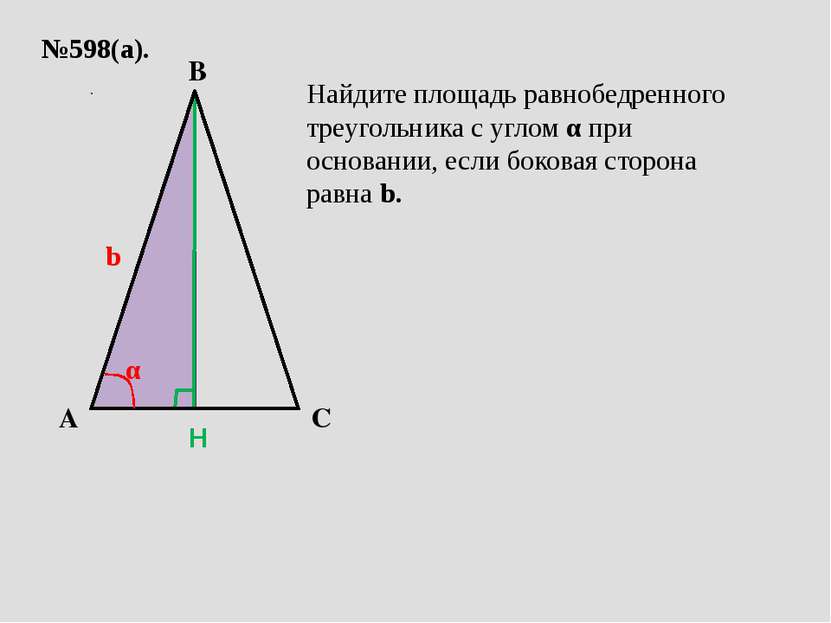
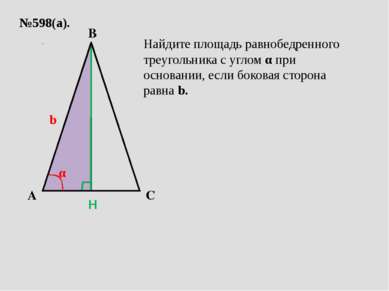№598(а). A C B b α Найдите площадь равнобедренного треугольника с углом α при основании, если боковая сторона равна b. H
Cлайд 12
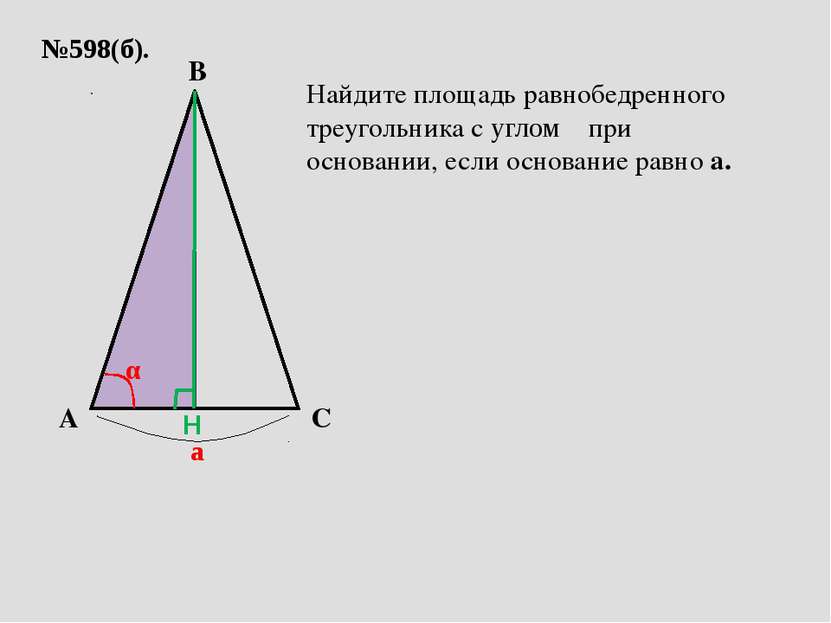
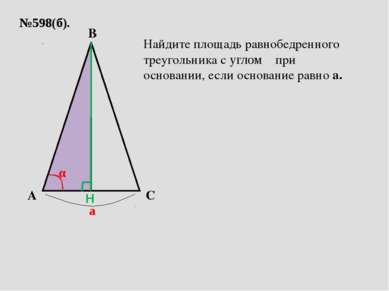№598(б). A C B а α Найдите площадь равнобедренного треугольника с углом α при основании, если основание равно а. H
Cлайд 13
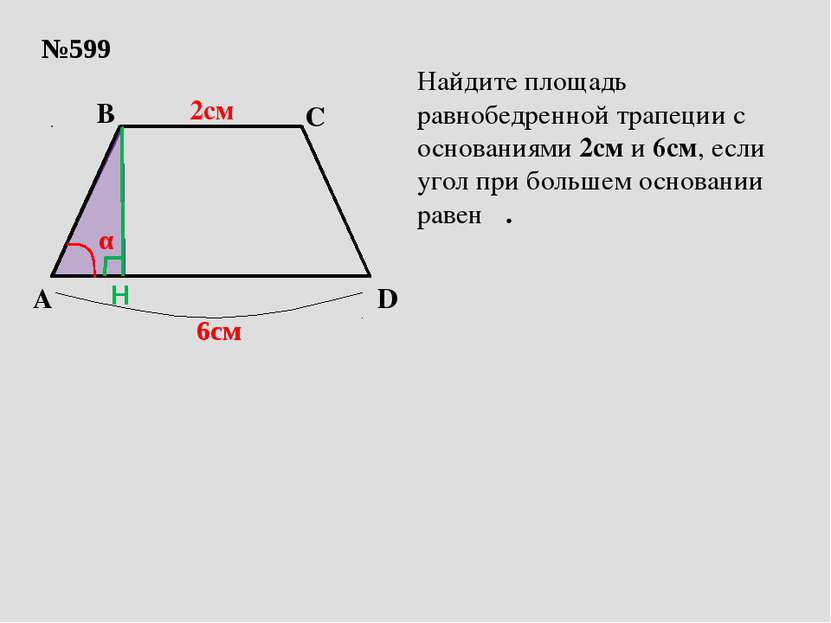
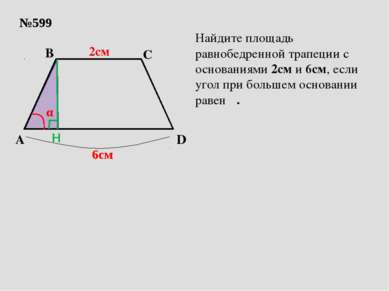№599 A B D C 2см 6см α Найдите площадь равнобедренной трапеции с основаниями 2см и 6см, если угол при большем основании равен α. H
Cлайд 14
№600 A B D C 60м ? Насыпь шоссейной дороги имеет в верхней части ширину 60 м. Какова ширина насыпи в нижней её части, если угол наклона откосов к горизонту равен 60°, а высота насыпи равна 12 м? 12м 60° 60° H
Cлайд 15
Домашнее задание П.66 , №597, №603 Спасибо за урок Информационные ресурсы Геометрия. 7—9 классы : учеб. для общеобразоват. учреждений /Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.— 20-е изд. — М. : Просвещение, 2010.
