X
Код презентации скопируйте его
Законы Кеплера (11 класс)
Скачать эту презентацию
Презентация на тему Законы Кеплера (11 класс)
Скачать эту презентациюCлайд 1
Презентация по физике на тему: Законы Кеплера Работа ученика 11 класса ГБОУ СОШ №1465 имени Н.Г. Кузнецова Шопорова Максима Учитель физики Л.Ю. Круглова
Cлайд 2
Оглавление Краткая биография стр.3 Формулировки стр.4-7 Формулы 8-11 Галерея
Cлайд 3
Перед рассказом про законы Кеплера, хотелось бы рассказать про их создателя Йоганна Кеплера. Перед рассказом про законы Кеплера, хотелось бы рассказать про их создателя Йоганна Кеплера. Иоганн Кеплер немецкий математик, астроном, механик, оптик и астролог, первооткрыватель законов движения планет Солнечной системы и просто молодец. Родился в 27 декабря 1571 года, Вейль-дер-Штадт. Интерес к астрономии появился у Кеплера ещё в детские годы, когда его мать показала впечатлительному мальчику яркую комету (1577), а позднее — лунное затмение (1580). Первоначально Кеплер планировал стать протестантским священником, но благодаря незаурядным математическим способностям был приглашён в 1594 году читать лекции по математике в университете города Граца. Так начался путь Кеплера, как ученого. Кеплер выпустил около 15 книг по астрономии. Несомненно Кеплер вложил большой вклад в развитие астрономии как XVI века, так и нынешней, ибо его законы лежат в основе многих теорий. Благодаря исследованиям Кеплера, ученый Бонавентура Кавальери разработал «Метод Неделимых». Завершением этого процесса стало открытие математического анализа. 15 ноября 1630 года Йоганн Кеплер умирает в городе Регенсбург от простуды.
Cлайд 4
Законы Кеплера Законы Кеплера — три эмпирических соотношения, интуитивно подобранных Иоганном Кеплером на основе анализа астрономических наблюдений Тихо Браге. Описывают идеализированную гелиоцентрическую орбиту планеты. В рамках классической механики выводятся из решения задачи двух тел предельным переходом / → 0, где , — массы планеты и Солнца соответственно. Законы были открыты в конце 16 века, когда шла борьба между геоцентрической системой Птолемея и гелиоцентрической системой Коперника.
Cлайд 5
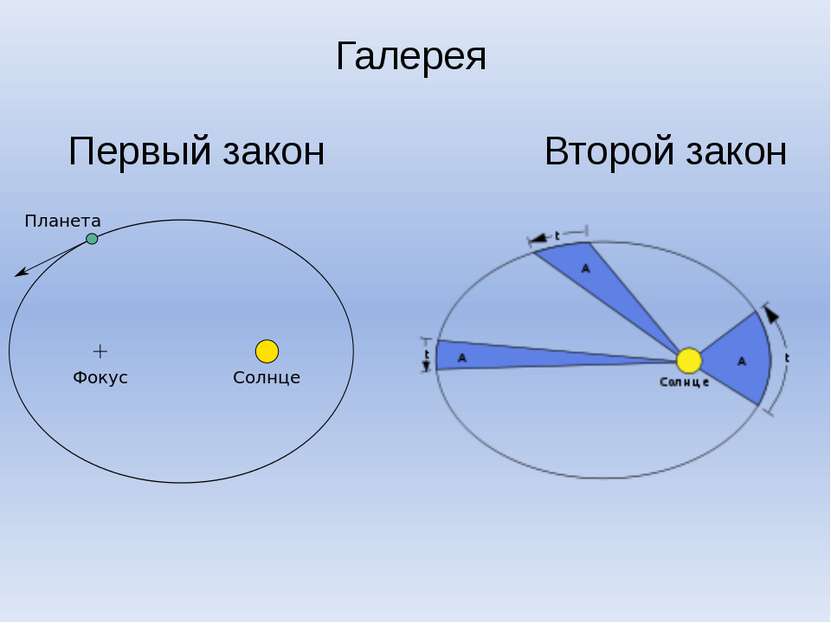
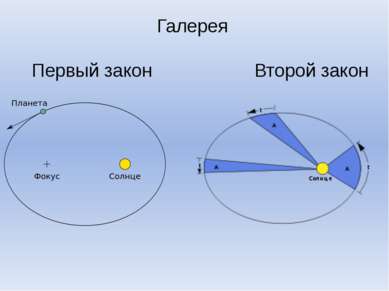
1-й закон Кеплера «Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце» Форма эллипса и степень его сходства с окружностью характеризуется отношением е=с/а , где с — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), а — большая полуось. Величина называется эксцентриситемом эллипса. При с=0, и, следовательно е=0 , эллипс превращается в окружность.
Cлайд 6
2-й закон Кеплера(закон площадей) «Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади» Применительно к нашей Солнечной системе, с этим законом связаны два понятия: перигелий— ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии. Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.
Cлайд 7
Третий закон Кеплера (гармонический закон) «Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет» Справедливо не только для планет, но и для их спутников. Ньютон установил, что грав. притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты. Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.
Cлайд 8
Формулы к законам Кеплера Первый закон: е=с\а – расстояние от центра до эллипса.
Cлайд 9
2-й закон По определению угловой момент L точечной частицы с массой m и скоростью v записывается в виде: .где r — радиус-вектор частицы а p=mv — импульс частицы. Площадь, заметаемая радиус-вектором r за время dt из геометрических соображений равна , где представляет собой угол между направлениями и . По определению .В результате мы имеем .Продифференцируем обе части уравнения по времени поскольку векторное произведение параллельных векторов равно нулю. Заметим, что F всегда параллелен r, поскольку сила радиальная, и p всегда параллелен v по определению. Таким образом можно утверждать, что |L|, а следовательно и пропорциональная ей скорость заметания площади ds\dt — константа.
Cлайд 10
2-ой закон Кеплера Второй закон Кеплера утверждает, что радиус-вектор обращающегося тела заметает равные площади за равные промежутки времени. Если теперь мы возьмём очень малые промежутки времени в момент, когда планета находится в точках A и B (перигелий и афелий), то мы сможем аппроксимировать площадь треугольниками с высотами, равными расстоянию от планеты до Солнца, и основанием, равным произведению скорости планеты на время.
Cлайд 11
, где Т1 и Т2 - периоды обращения двух планет вокруг Солнца, а а1 и а2 — длины больших полуосей их орбит. , где Т1 и Т2 - периоды обращения двух планет вокруг Солнца, а а1 и а2 — длины больших полуосей их орбит. Третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты: ,где М-масса солнца, а м1 и м2- массы планет
Cлайд 12
Галерея Первый закон Второй закон
