X
Код презентации скопируйте его
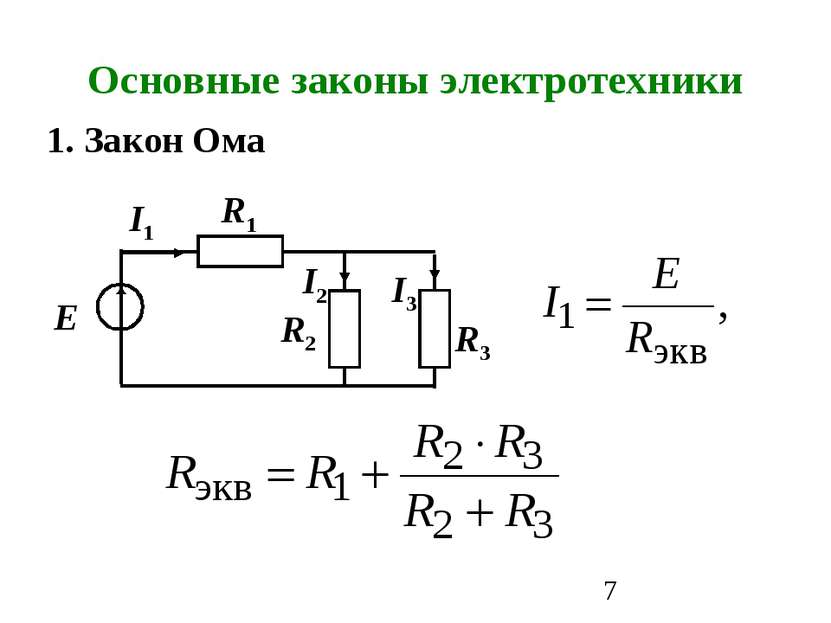
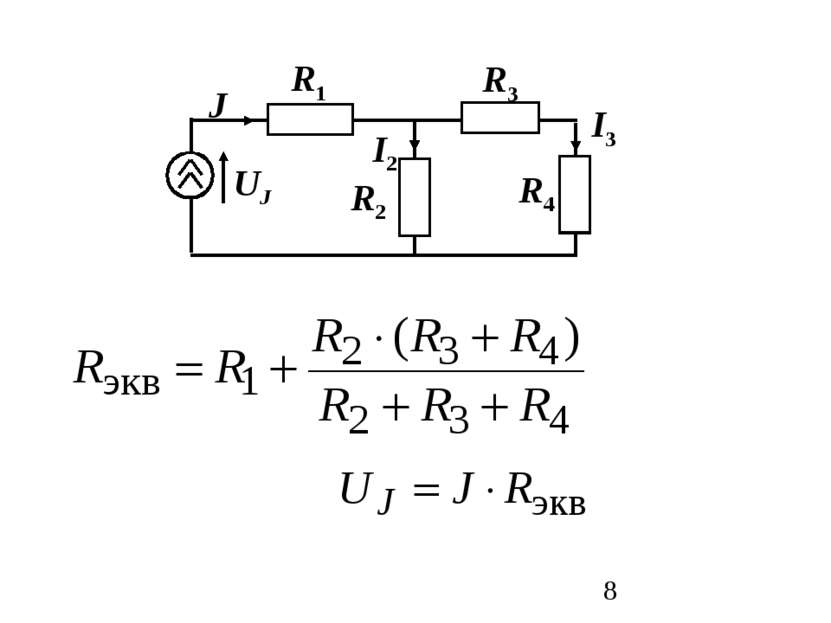
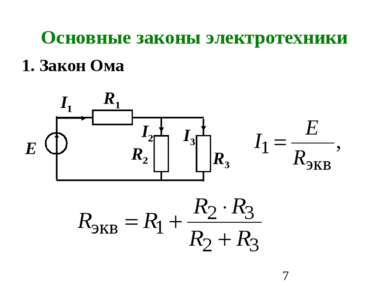
Основные законы электротехники
Скачать эту презентациюПрезентация на тему Основные законы электротехники
Скачать эту презентациюCлайд 2
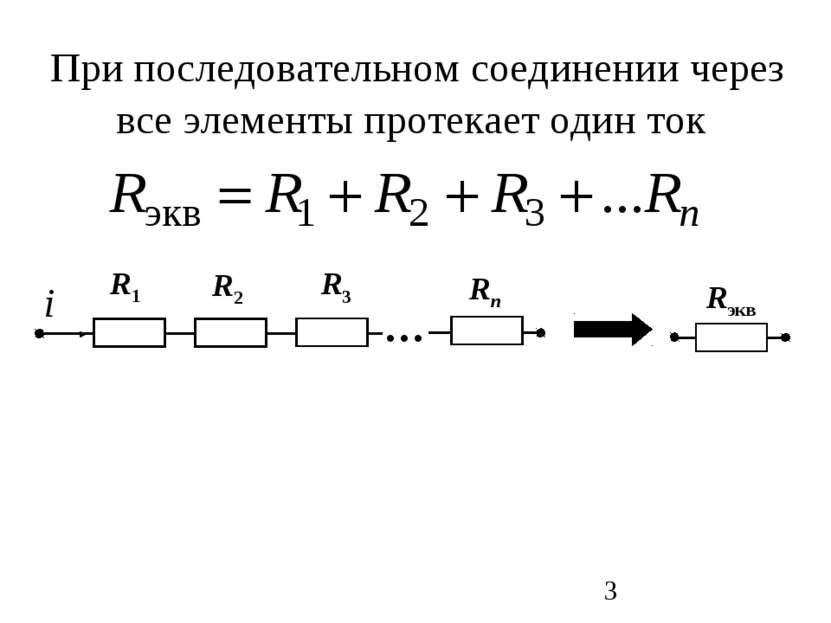
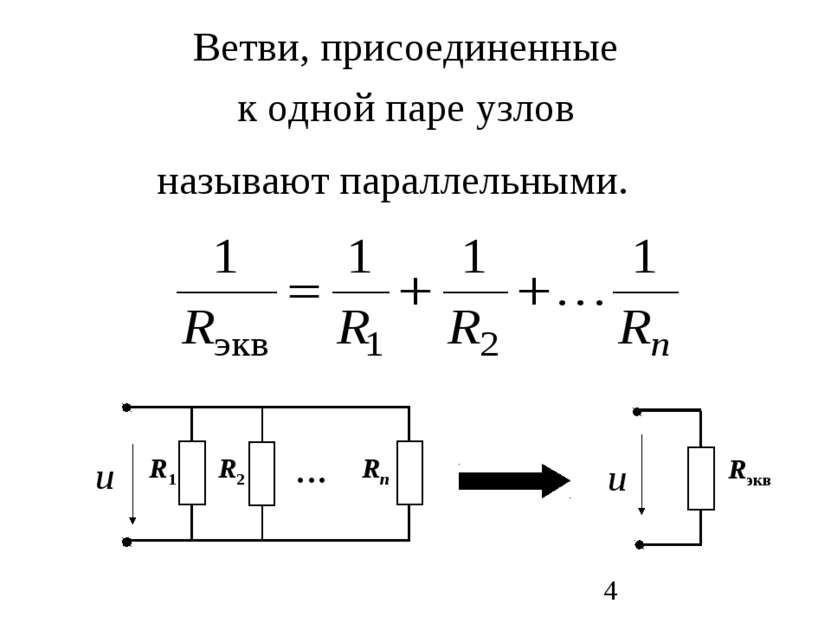
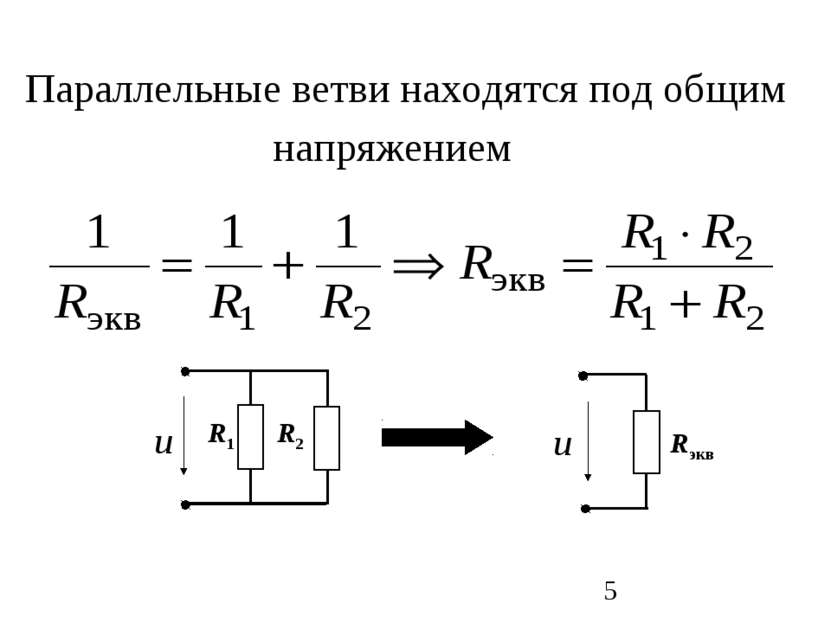
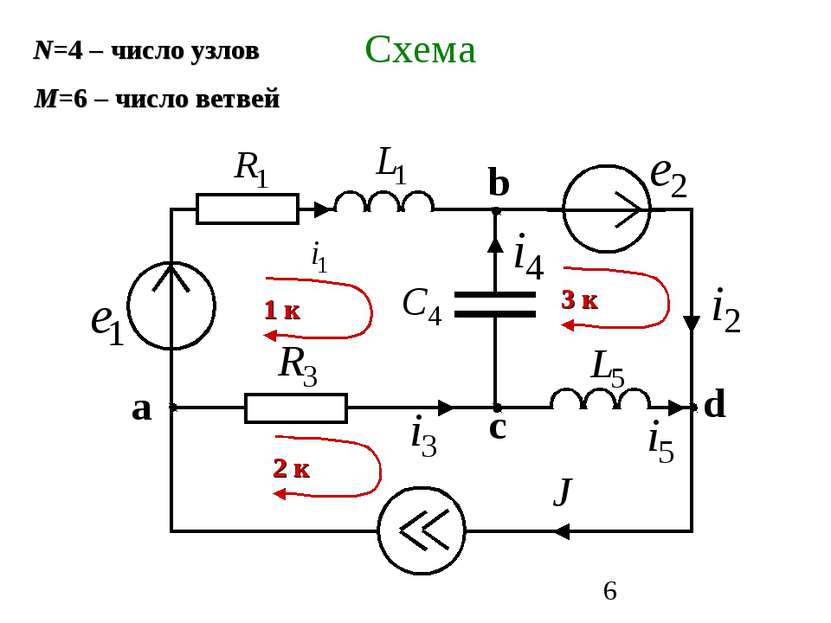
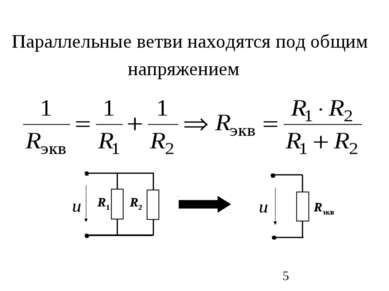
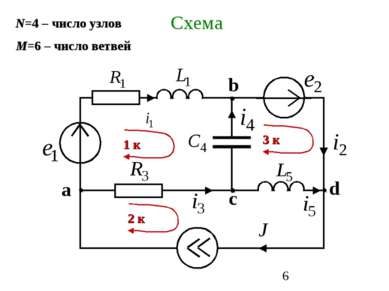
 Схема – это графическое изображение электрической цепи. Ветвь – это участок схемы, вдоль которого течет один и тот же ток. Узел – это место соединения трех или большего числа ветвей Контур – это замкнутый путь, проходящий по нескольким ветвям Независимый контур – это контур, у которого хотя бы одна ветвь не принадлежит другим контурам
Схема – это графическое изображение электрической цепи. Ветвь – это участок схемы, вдоль которого течет один и тот же ток. Узел – это место соединения трех или большего числа ветвей Контур – это замкнутый путь, проходящий по нескольким ветвям Независимый контур – это контур, у которого хотя бы одна ветвь не принадлежит другим контурам
Cлайд 9
 Законы Кирхгофа Кирхгоф (Kirchhoff) Густав Роберт 1824-1887г. немецкий физик, член Берлинской АН, член-корреспондент Петербургской АН. В возрасте двадцати одного года, сформулировал основные законы для расчета токов и напряжений в электрических цепях
Законы Кирхгофа Кирхгоф (Kirchhoff) Густав Роберт 1824-1887г. немецкий физик, член Берлинской АН, член-корреспондент Петербургской АН. В возрасте двадцати одного года, сформулировал основные законы для расчета токов и напряжений в электрических цепях
Cлайд 10
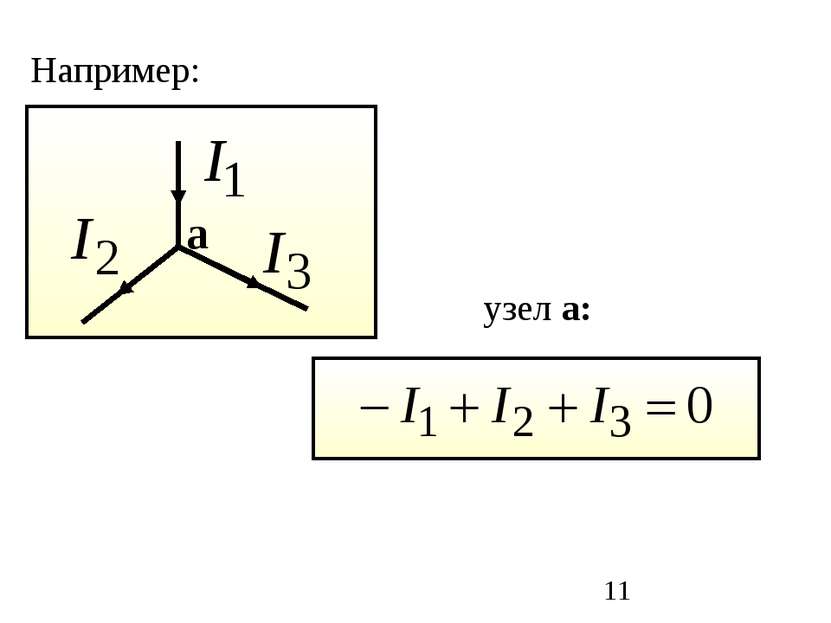
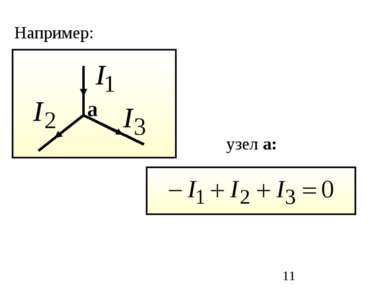
 Первый закон Кирхгофа: алгебраическая сумма токов в узле равняется нулю (токи, вытекающие из узла, считаются положительными, а втекающие – отрицательными): Физический смысл этого закона прост: если бы он не выполнялся, в узле непрерывно накапливался бы электрический заряд, а этого никогда не происходит.
Первый закон Кирхгофа: алгебраическая сумма токов в узле равняется нулю (токи, вытекающие из узла, считаются положительными, а втекающие – отрицательными): Физический смысл этого закона прост: если бы он не выполнялся, в узле непрерывно накапливался бы электрический заряд, а этого никогда не происходит.
Cлайд 12
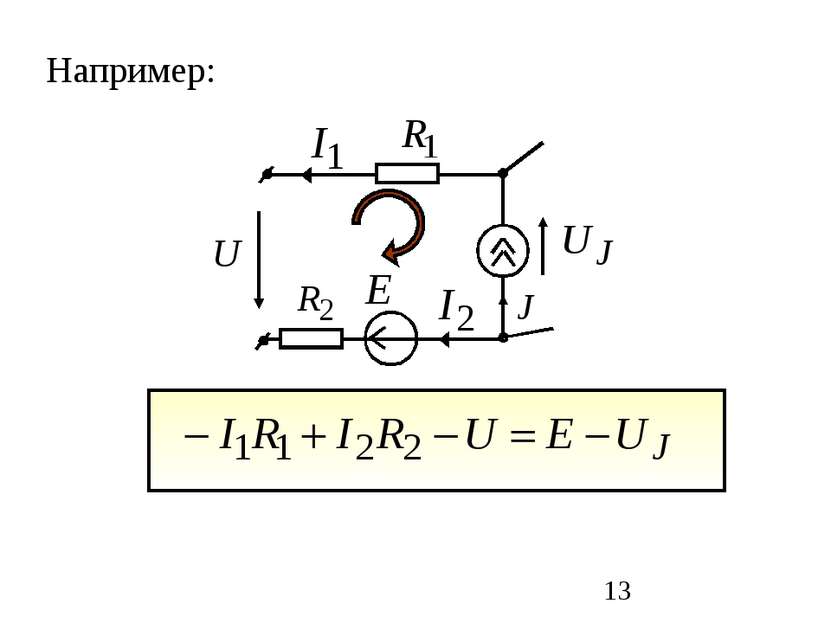
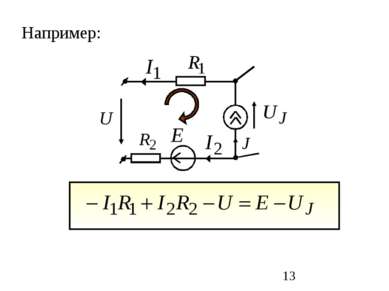
 Второй закон Кирхгофа: в контуре алгебраическая сумма падений напряжения на пассивных элементах равна алгебраической сумме ЭДС и напряжений на зажимах источников тока. с “+” берутся все слагаемые, положительное направление которых совпадает с выбранным обходом контура:
Второй закон Кирхгофа: в контуре алгебраическая сумма падений напряжения на пассивных элементах равна алгебраической сумме ЭДС и напряжений на зажимах источников тока. с “+” берутся все слагаемые, положительное направление которых совпадает с выбранным обходом контура:
Cлайд 14
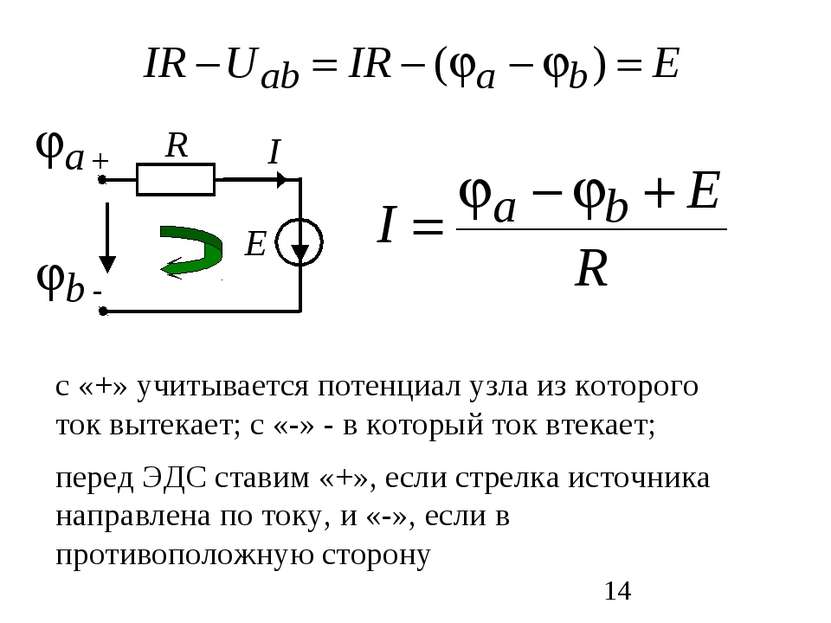
 Е R I с «+» учитывается потенциал узла из которого ток вытекает; с «-» - в который ток втекает; перед ЭДС ставим «+», если стрелка источника направлена по току, и «-», если в противоположную сторону + -
Е R I с «+» учитывается потенциал узла из которого ток вытекает; с «-» - в который ток втекает; перед ЭДС ставим «+», если стрелка источника направлена по току, и «-», если в противоположную сторону + -
Cлайд 15
 1. Метод законов Кирхгофа Решение системы уравнений, составленных по законам Кирхгофа, позволяет определить все токи и напряжения в рассматриваемой цепи
1. Метод законов Кирхгофа Решение системы уравнений, составленных по законам Кирхгофа, позволяет определить все токи и напряжения в рассматриваемой цепи
Cлайд 20
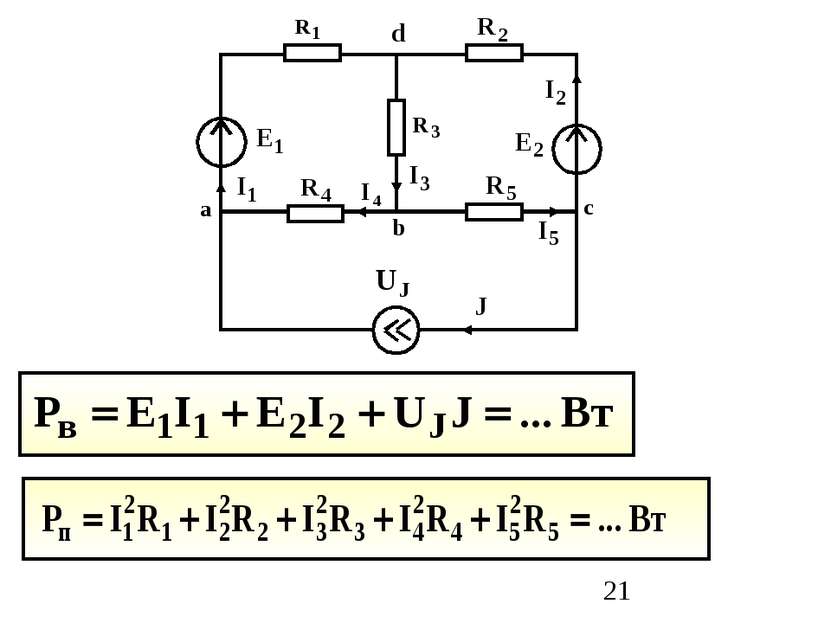
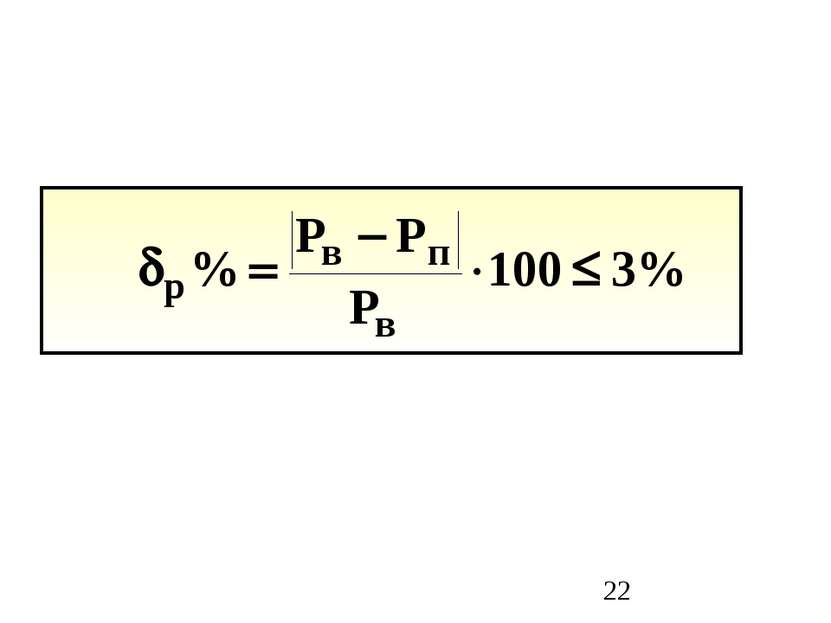
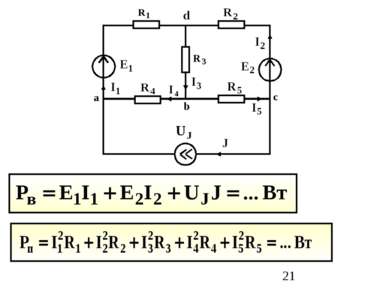
 Для любого момента времени сумма вырабатываемых мощностей источников равна сумме потребляемых мощностей во всех пассивных элементах рассматриваемой цепи Теорема Телледжена:
Для любого момента времени сумма вырабатываемых мощностей источников равна сумме потребляемых мощностей во всех пассивных элементах рассматриваемой цепи Теорема Телледжена:
Cлайд 24
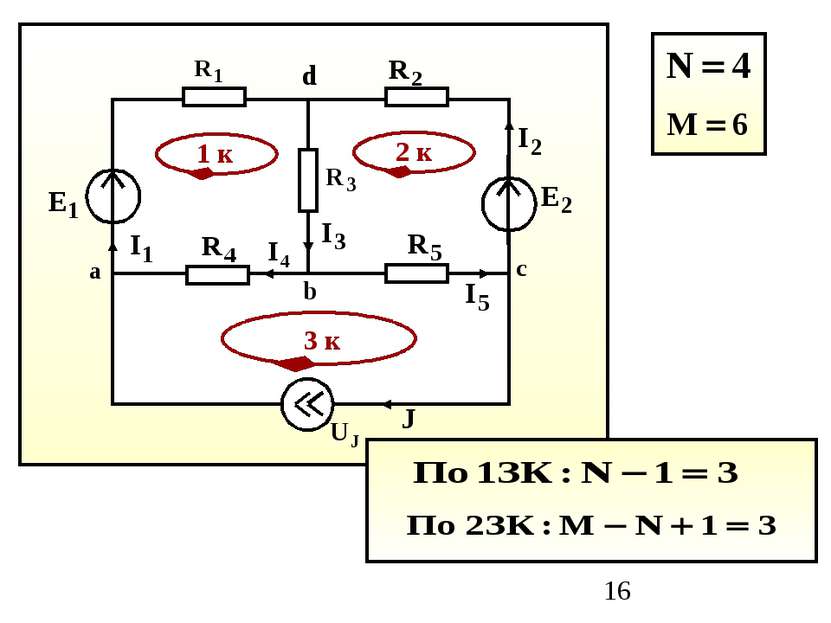
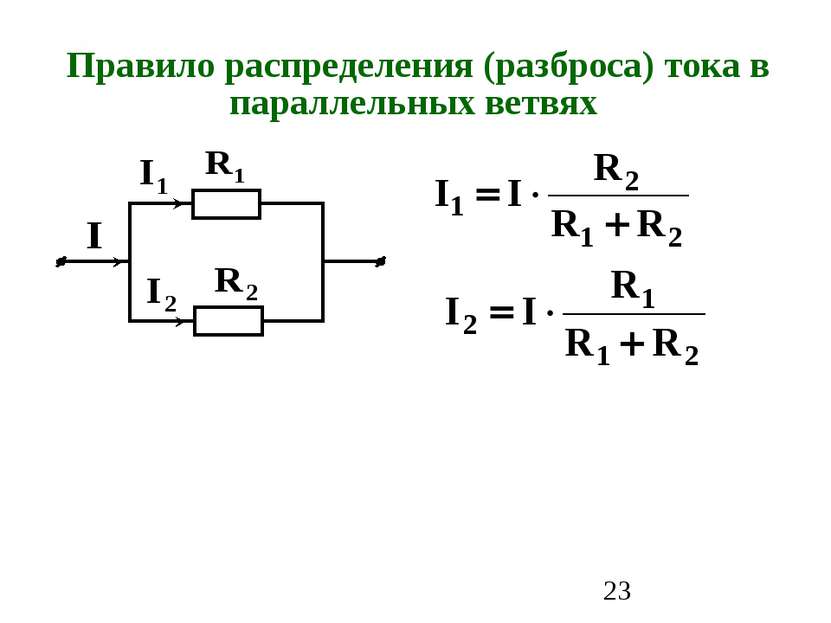
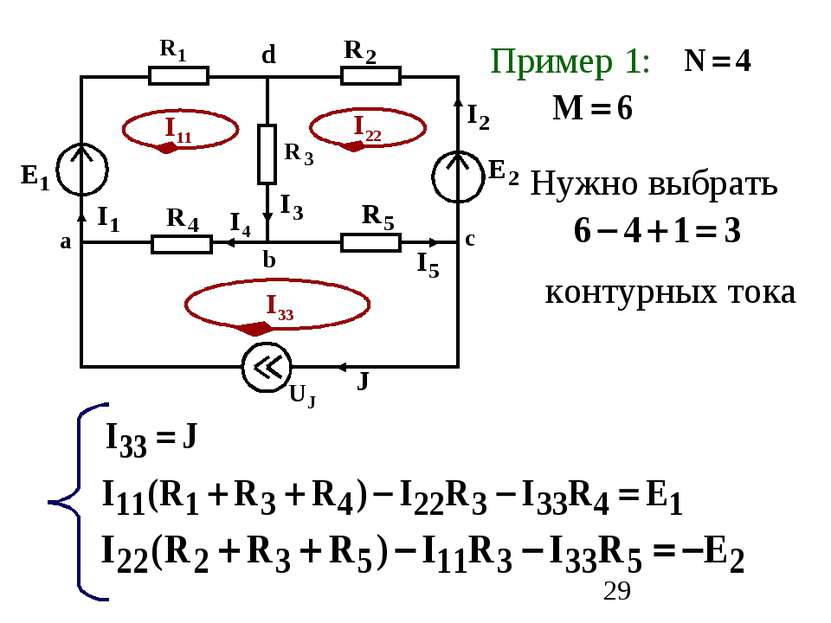
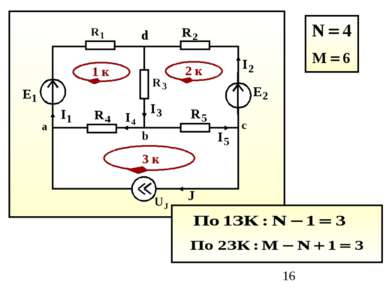
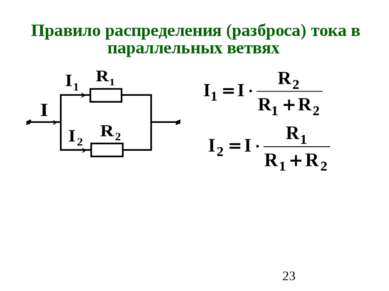
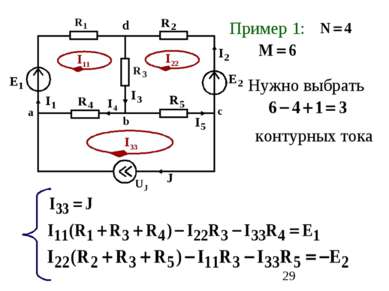
 2. Метод контурных токов Основан на решении уравнений, составленных по второму закону Кирхгофа и позволяет уменьшить порядок системы уравнений Контурный ток – это ток, текущий в независимом контуре. Число уравнений равно числу независимых контуров: M-N+1
2. Метод контурных токов Основан на решении уравнений, составленных по второму закону Кирхгофа и позволяет уменьшить порядок системы уравнений Контурный ток – это ток, текущий в независимом контуре. Число уравнений равно числу независимых контуров: M-N+1
Cлайд 26
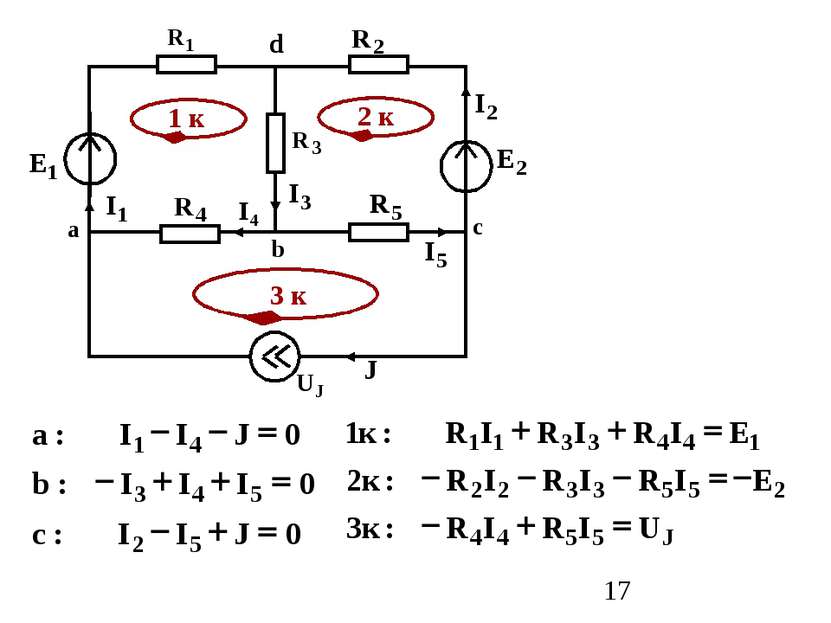
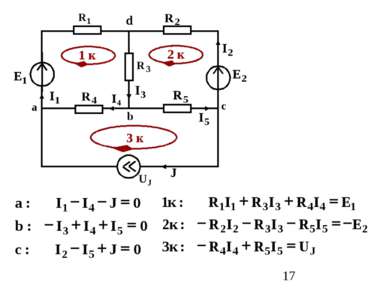
 Алгоритм составления уравнений Контурный ток рассматриваемого контура умножается на сумму сопротивлений этого контура. 2. К этому произведению дописываются произведения всех соседних контурных токов на общие сопротивления (c “+” если контурные токи обтекают общее сопротивление в одном направлении). 3. В правой части уравнения записывается алгебраическая сумма ЭДС контура (с “+”, если направление ЭДС совпадает с направлением контурного тока.
Алгоритм составления уравнений Контурный ток рассматриваемого контура умножается на сумму сопротивлений этого контура. 2. К этому произведению дописываются произведения всех соседних контурных токов на общие сопротивления (c “+” если контурные токи обтекают общее сопротивление в одном направлении). 3. В правой части уравнения записывается алгебраическая сумма ЭДС контура (с “+”, если направление ЭДС совпадает с направлением контурного тока.
Cлайд 27
 Важно!!! Для контура с источником тока уравнение не составляется, так как контурный ток будет равен току источника тока, через источник тока должен проходить только один контурный ток.
Важно!!! Для контура с источником тока уравнение не составляется, так как контурный ток будет равен току источника тока, через источник тока должен проходить только один контурный ток.
Cлайд 28
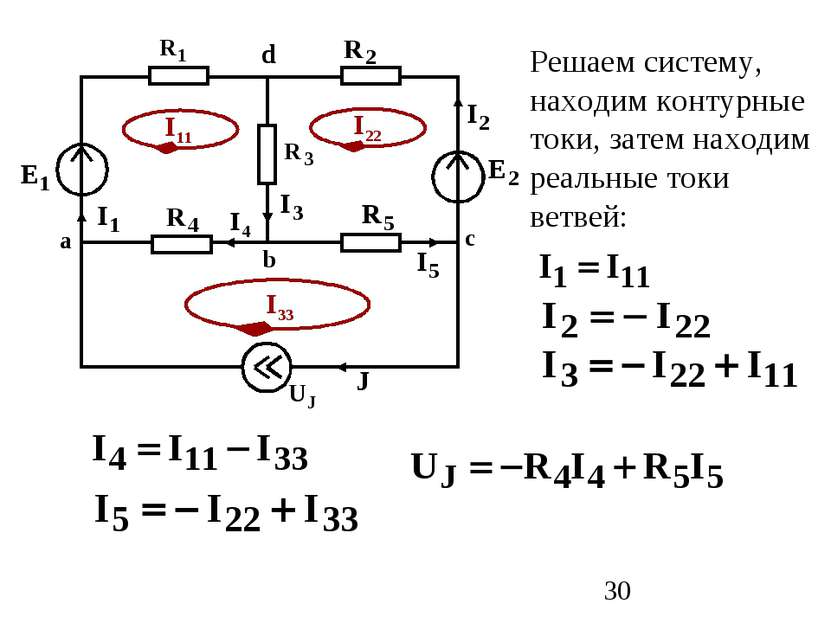
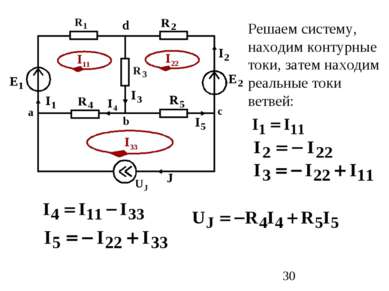
 Порядок расчета Обозначаются токи ветвей Выбираются контурные токи Составляется система уравнений по алгоритму Находятся контурные токи Через контурные токи находятся реальные токи схемы
Порядок расчета Обозначаются токи ветвей Выбираются контурные токи Составляется система уравнений по алгоритму Находятся контурные токи Через контурные токи находятся реальные токи схемы
Cлайд 31
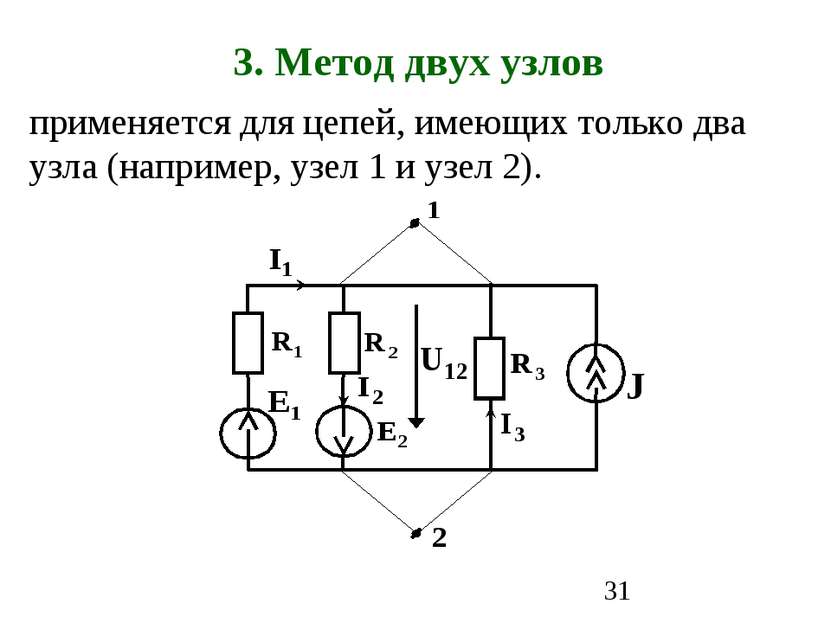
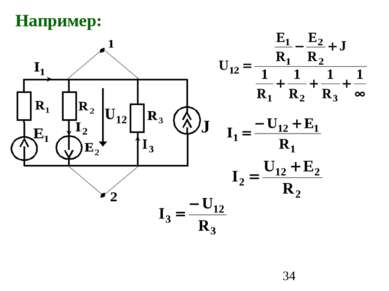
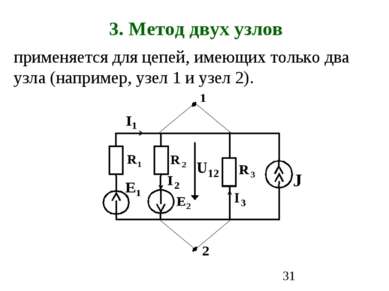 3. Метод двух узлов применяется для цепей, имеющих только два узла (например, узел 1 и узел 2).
3. Метод двух узлов применяется для цепей, имеющих только два узла (например, узел 1 и узел 2).
Cлайд 32
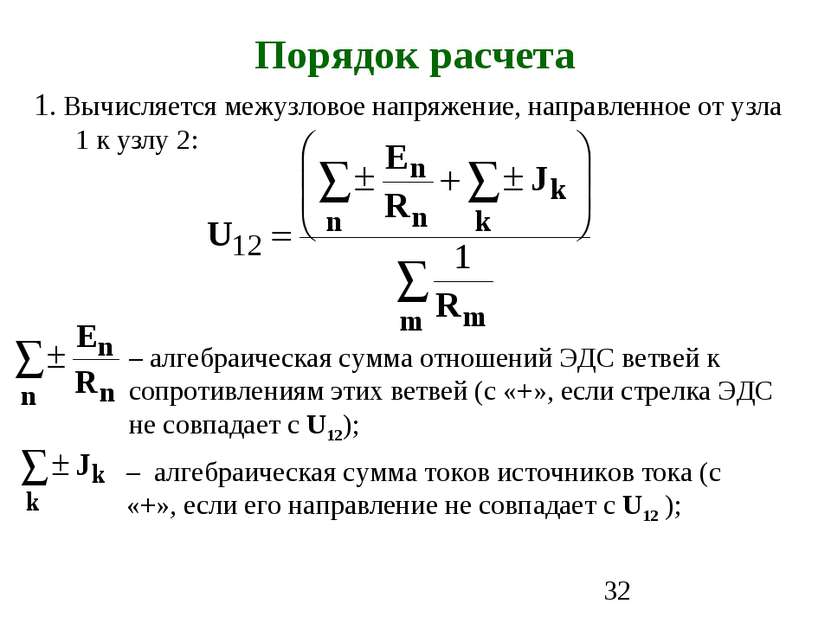
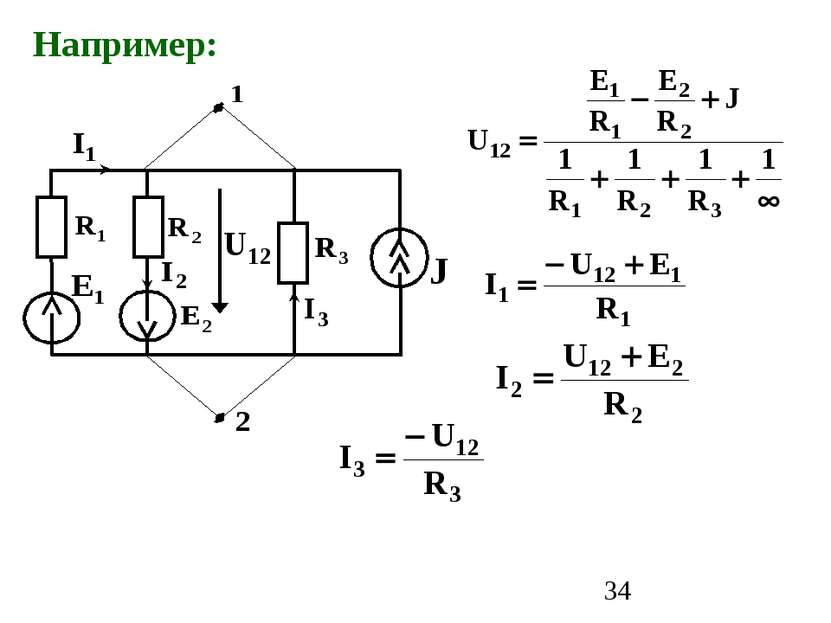
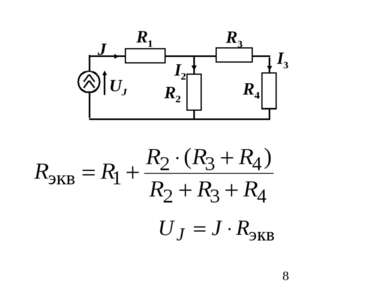
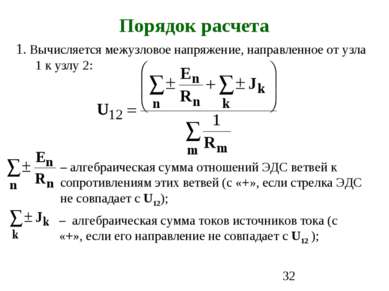 1. Вычисляется межузловое напряжение, направленное от узла 1 к узлу 2: – алгебраическая сумма отношений ЭДС ветвей к сопротивлениям этих ветвей (с «+», если стрелка ЭДС не совпадает с U12); – алгебраическая сумма токов источников тока (с «+», если его направление не совпадает с U12 ); Порядок расчета
1. Вычисляется межузловое напряжение, направленное от узла 1 к узлу 2: – алгебраическая сумма отношений ЭДС ветвей к сопротивлениям этих ветвей (с «+», если стрелка ЭДС не совпадает с U12); – алгебраическая сумма токов источников тока (с «+», если его направление не совпадает с U12 ); Порядок расчета