X
Код презентации скопируйте его
Квадратные уравнения 8 класс
Скачать эту презентацию
Презентация на тему Квадратные уравнения 8 класс
Скачать эту презентациюCлайд 1
АЛГЕБРА, 8 класс Тема урока: «Квадратные уравнения» МОУ Клявлинская СОШ №2 Автор: Венюкова Л.А.
Cлайд 2
Если ты услышишь, что кто-то не любит математику, не верь. Её нельзя не любить - её можно только не знать.
Cлайд 3
уравнение вида ах2 + вх +с = 0, где х –переменная, а, в и с некоторые числа, причем а 0. ОПРЕДЕЛЕНИЕ: Квадратным уравнением называется
Cлайд 4
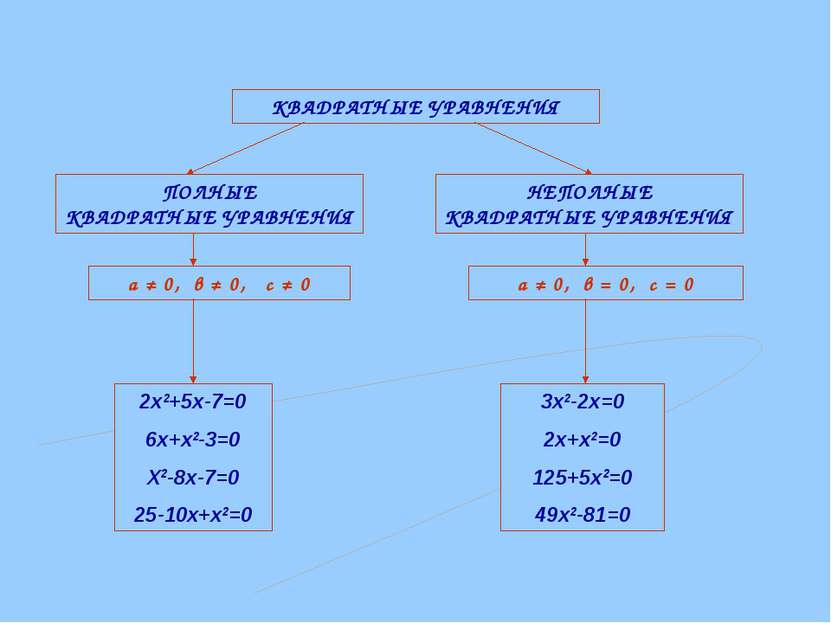
ПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ КВАДРАТНЫЕ УРАВНЕНИЯ а ≠ 0, в ≠ 0, с ≠ 0 а ≠ 0, в = 0, с = 0 2х2+5х-7=0 6х+х2-3=0 Х2-8х-7=0 25-10х+х2=0 3х2-2х=0 2х+х2=0 125+5х2=0 49х2-81=0
Cлайд 5
а) 6х2 – х + 4 = 0 б) 12х - х2 + 7 = 0 в) 8 + 5х2 = 0 г) х – 6х2 = 0 д) - х + х2 = 15 а = 6, в = -1, с = 4; а = -1, в = 12, с = 7; а = 5, в = 0, с = 8; а = -6, в =1, с = 0; а = 1, в =-1, с = -15. Определите коэффициенты квадратного уравнения:
Cлайд 6
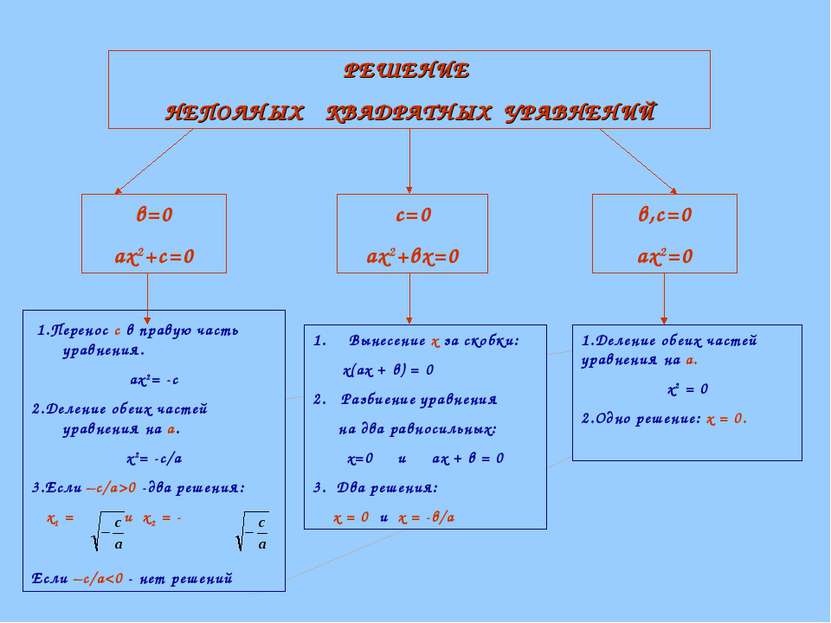
РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ в=0 ах2+с=0 с=0 ах2+вх=0 в,с=0 ах2=0 1.Перенос с в правую часть уравнения. ах2= -с 2.Деление обеих частей уравнения на а. х2= -с/а 3.Если –с/а>0 -два решения: х1 = и х2 = - Если –с/а
Cлайд 7
РЕШИ САМОСТОЯТЕЛЬНО УРАВНЕНИЯ : 1 вариант: а) б) ( х + 2)2 + ( х -3)2 = 13 2 вариант: а) 2х + х2= 0 б) 49х2 – 81 = 0 3 вариант: а) 3х2 – 2х = 0 б) 125 + 5х2 = 0
Cлайд 8
Способы решения полных квадратных уравнений Выделение квадрата двучлена. Формула: D = b2- 4ac, x1,2= График. Теорема Виета.
Cлайд 9
РЕШИ УРАВНЕНИЯ способом выделения квадрата двучлена : 1 вариант: - х + 3х2 – 70 =0 2 вариант: 2х2 -9х + 10 = 0 3 вариант: х2 – 8х -9 = 0
Cлайд 10
РЕШИ УРАВНЕНИЯ с помощью формулы : 1 вариант: а) -7х + 5х2 + 1 =0 б) (х – 1)(х + 1) = 2 (5х – 10,5) 2 вариант: а) 2х2 + 5х -7 = 0 б) –х2 = 5х - 14 3 вариант: а) х2 – 8х + 7 = 0 б) 6х – 9 = х2
Cлайд 11
РЕШИ УРАВНЕНИЯ графически : 1 вариант: 1/3х2 -х = - 2/3 2 вариант: а) х2 + 1,5х = 2,5 3 вариант: а) 6х + х2– 3 =0
Cлайд 12
Исторические сведения: Квадратные уравнения впервые встречаются в работе индийского математика и астронома Ариабхатты. Другой индийский ученый Брахмагупта (VII в) изложил общее правило решения квадратных уравнений, которое практически совпадает с современным. В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную форму. ________________________________________________ Вот задача Бхаскары: Обезьянок резвых стая, всласть поевши, развлекалась. Их в квадрате часть восьмая на полянке забавлялась. А двенадцать по лианам стали прыгать, повисая. Сколько ж было обезьянок, ты скажи мне, в этой стае?
Cлайд 13
Решение задачи Бхаскары: Пусть было x обезьянок, тогда на поляне забавлялось – . Составим уравнение: + 12 = х Ответ: х1= 16 , х2= 48 обезьянок.
