X
Код презентации скопируйте его
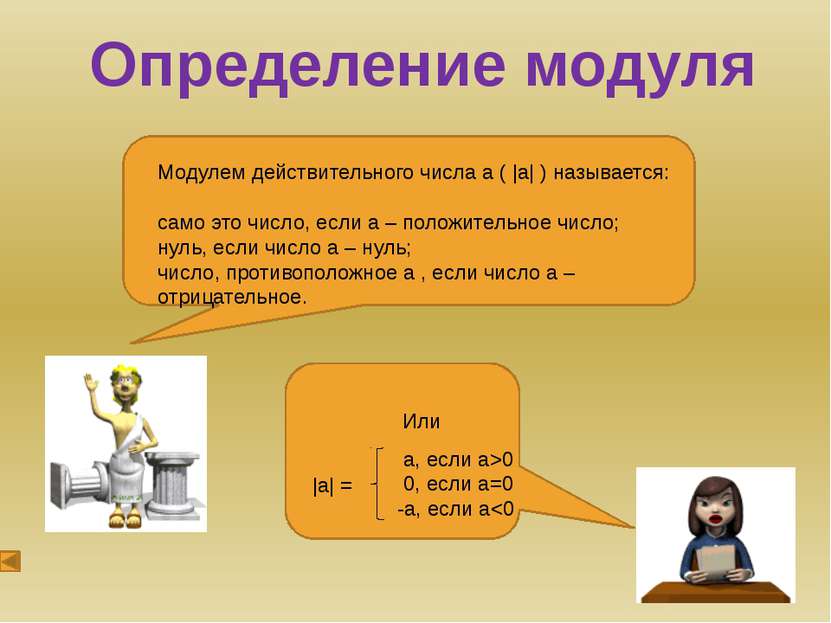
Решение уравнений и неравенств, содержащих модуль, методом интервалов
Скачать эту презентациюПрезентация на тему Решение уравнений и неравенств, содержащих модуль, методом интервалов
Скачать эту презентациюCлайд 8
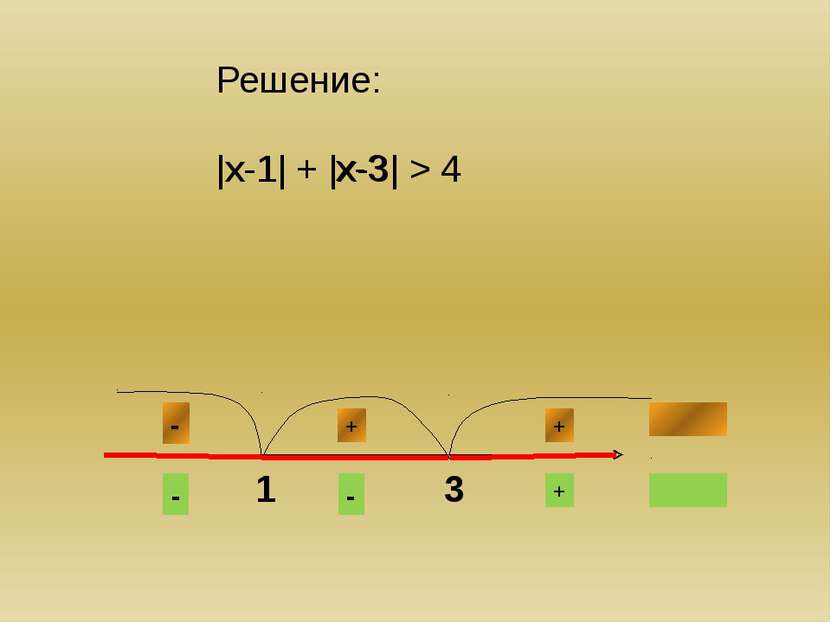
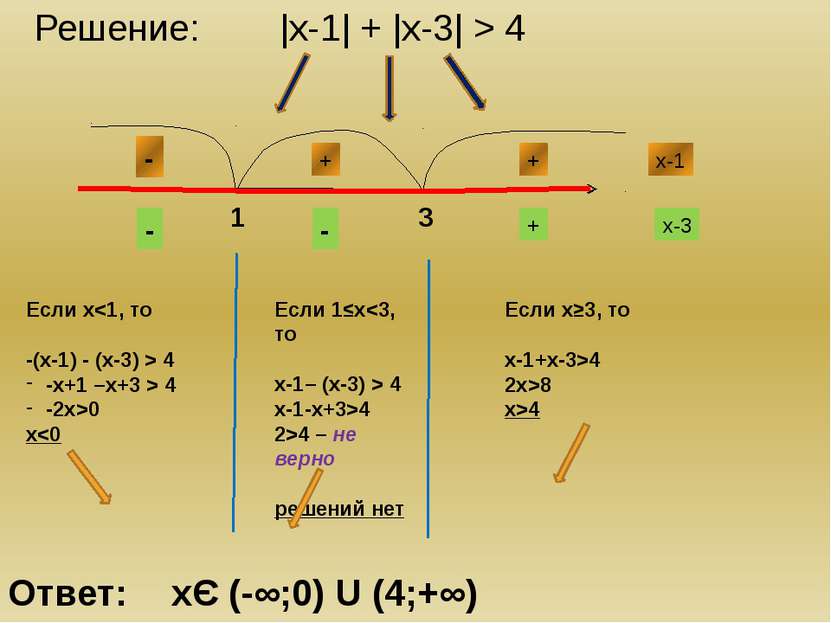
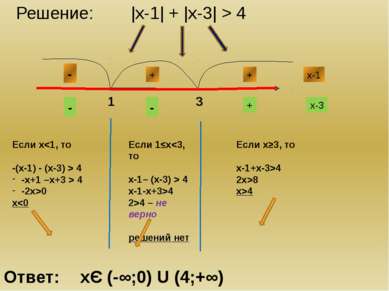
 Решение: |х-1| + |х-3| > 4 Если х 4 -х+1 –х+3 > 4 -2х>0 х4 2>4 – не верно решений нет Если х≥3, то х-1+х-3>4 2х>8 х>4 Ответ: хЄ (-∞;0) U (4;+∞) х-1 - + + х-3 + - -
Решение: |х-1| + |х-3| > 4 Если х 4 -х+1 –х+3 > 4 -2х>0 х4 2>4 – не верно решений нет Если х≥3, то х-1+х-3>4 2х>8 х>4 Ответ: хЄ (-∞;0) U (4;+∞) х-1 - + + х-3 + - -
Cлайд 9
 Общий алгоритм найти нули подмодульных выражений и отметить их на числовой прямой определить знаки подмодульных выражений на полученных промежутках на каждом промежутке решить уравнение ( неравенство ) объединить полученные решения
Общий алгоритм найти нули подмодульных выражений и отметить их на числовой прямой определить знаки подмодульных выражений на полученных промежутках на каждом промежутке решить уравнение ( неравенство ) объединить полученные решения
Cлайд 10
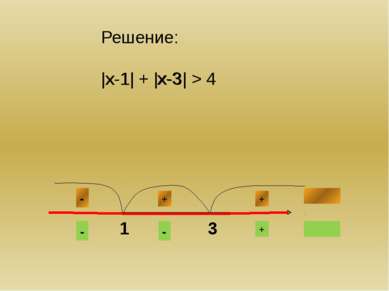 Большое количество ошибок при решении задач с модулями вызвано тем, что многие, освобождаясь от модуля, забывают учесть условия, при которых модуль был раскрыт с тем или иным знаком.
Большое количество ошибок при решении задач с модулями вызвано тем, что многие, освобождаясь от модуля, забывают учесть условия, при которых модуль был раскрыт с тем или иным знаком.