X
Код презентации скопируйте его
Исследование математических моделей
Скачать эту презентациюПрезентация на тему Исследование математических моделей
Скачать эту презентациюCлайд 2
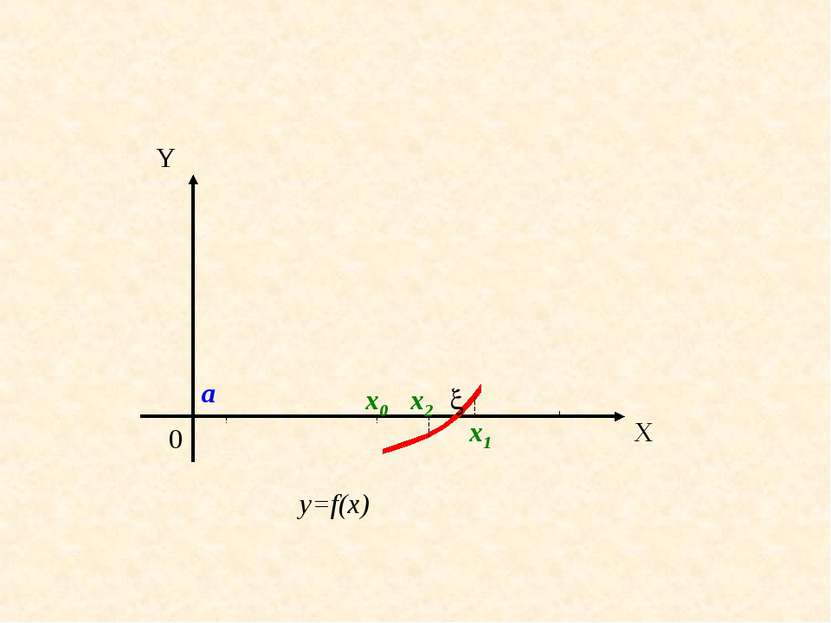
 Пусть задана функция f(x). Требуется найти корни уравнения f (x)=0 (1) Задача нахождения корней уравнения (1) обычно решается в два этапа. На первом этапе изучается расположение корней и проводится их разделение, то есть выделяются области, содержащие только один корень. На втором этапе, используя начальное приближение, строится итерационный процесс для уточнений корня.
Пусть задана функция f(x). Требуется найти корни уравнения f (x)=0 (1) Задача нахождения корней уравнения (1) обычно решается в два этапа. На первом этапе изучается расположение корней и проводится их разделение, то есть выделяются области, содержащие только один корень. На втором этапе, используя начальное приближение, строится итерационный процесс для уточнений корня.
Cлайд 3
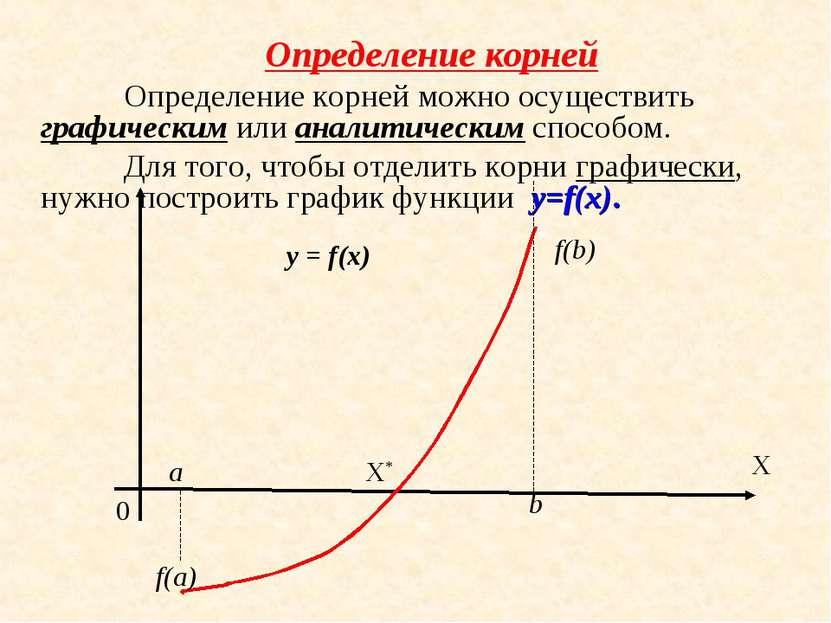
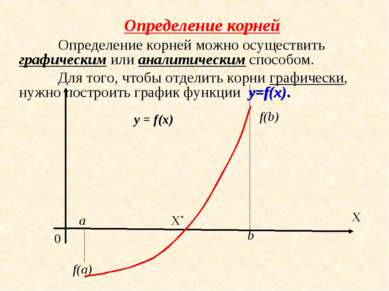 Определение корней Определение корней можно осуществить графическим или аналитическим способом. Для того, чтобы отделить корни графически, нужно построить график функции y=f(x). X 0 a b f(a) f(b) X* y = f(x)
Определение корней Определение корней можно осуществить графическим или аналитическим способом. Для того, чтобы отделить корни графически, нужно построить график функции y=f(x). X 0 a b f(a) f(b) X* y = f(x)
Cлайд 4
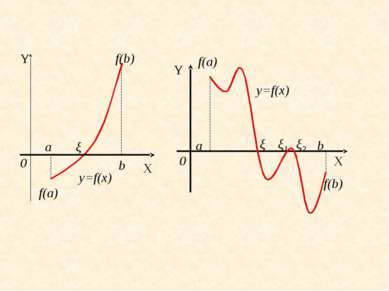
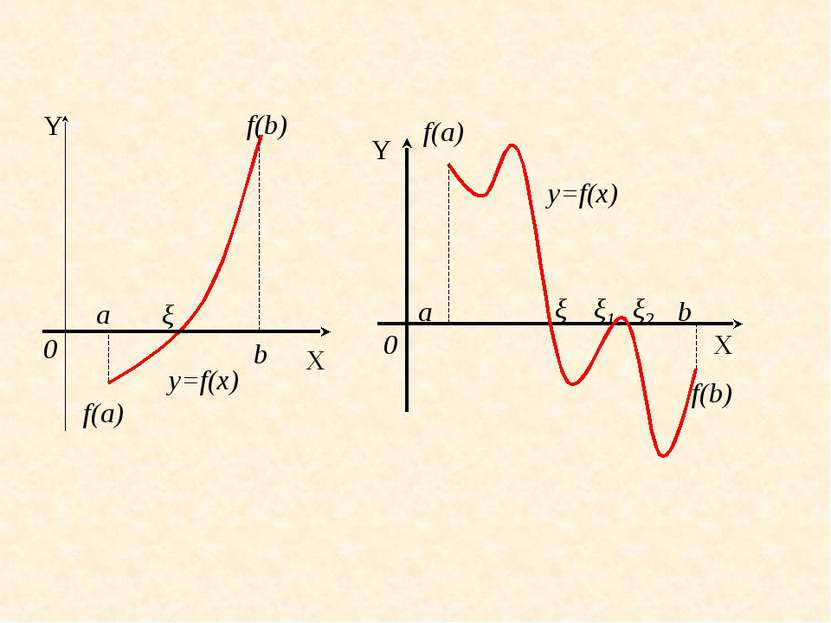
 Для определения корней аналитически используем следующее утверждение: если функция f(x) принимает значения разных знаков на концах отрезка [a, b], т.е. f(a) f(b)
Для определения корней аналитически используем следующее утверждение: если функция f(x) принимает значения разных знаков на концах отрезка [a, b], т.е. f(a) f(b)
Cлайд 6
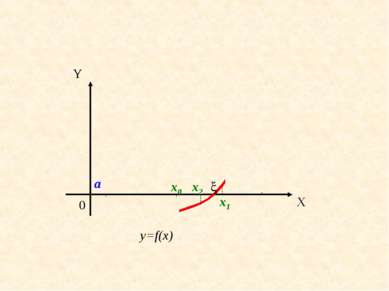
![Метод половинного деления Предположим что в интервале [a, b] расположен один ... Метод половинного деления Предположим что в интервале [a, b] расположен один ...](https://bigslide.ru/images/18/17115/389/img5.jpg) Метод половинного деления Предположим что в интервале [a, b] расположен один корень уравнения (1). Найдем точку c= (b+a) /2. Это x0. Далее, если f( c)* f( a) >0, то b = c, если f( c)* f( b) >0, то a = c. Аналогично находим следующие приближения xn (n=1,2,…) Если выполняется одно из условий : | f(xn+1) | или | xn-xn+1 | , где - заданная точность вычислений, то корень уравнения f(x)=0 найден =x*= xn+1 и процесс вычисления заканчивается.
Метод половинного деления Предположим что в интервале [a, b] расположен один корень уравнения (1). Найдем точку c= (b+a) /2. Это x0. Далее, если f( c)* f( a) >0, то b = c, если f( c)* f( b) >0, то a = c. Аналогично находим следующие приближения xn (n=1,2,…) Если выполняется одно из условий : | f(xn+1) | или | xn-xn+1 | , где - заданная точность вычислений, то корень уравнения f(x)=0 найден =x*= xn+1 и процесс вычисления заканчивается.




![Метод половинного деления Предположим что в интервале [a, b] расположен один ... Метод половинного деления Предположим что в интервале [a, b] расположен один ...](https://bigslide.ru/images/18/17115/831/img5.jpg)