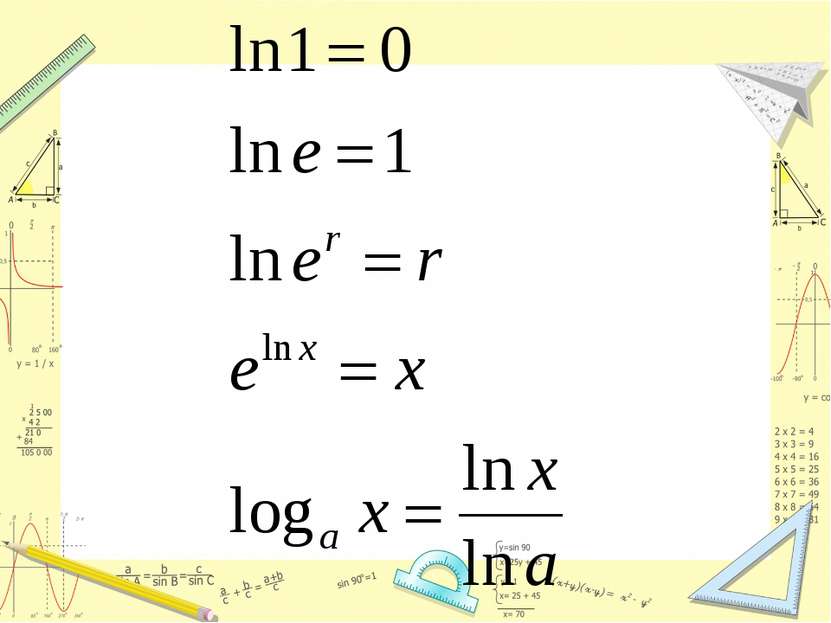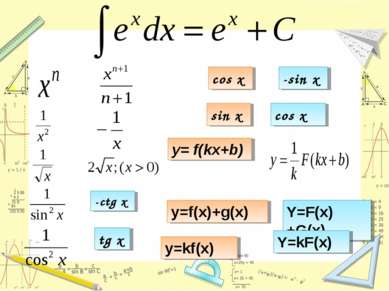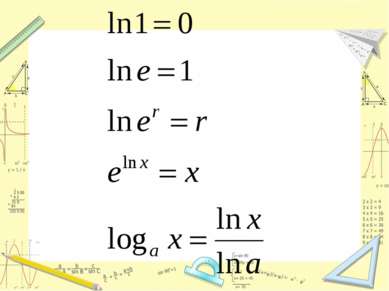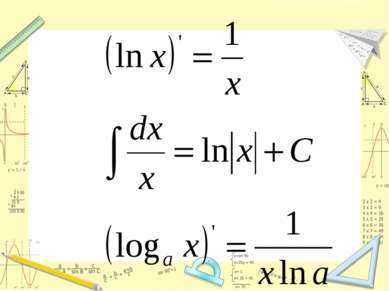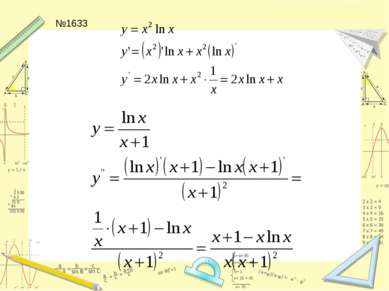X
Код презентации скопируйте его
Натуральные логарифмы
Скачать эту презентацию
Презентация на тему Натуральные логарифмы
Скачать эту презентациюCлайд 1
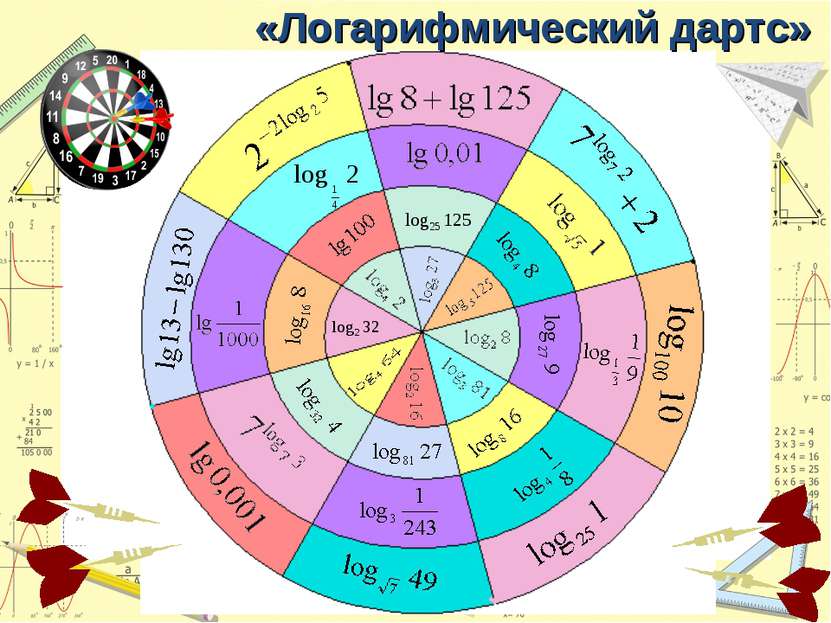
Натуральные логарифмы Расширить понятие логарифма, для этого введя понятие натурального логарифма, выяснить взаимное расположение графиков функции натурального логарифма и показательной, научиться использовать свойства для вычисления натуральных логарифмов Математика
Cлайд 2
«Логарифмический дартс»
Cлайд 3
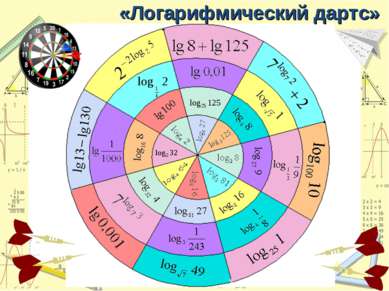
7 121 0,04 4 0,1 3 -4 4 -2 0 -5 7 4 2 4 4 -5 1 11 2 12 3 13 4 14 5 15 6 16 7 17 8 18 9 19 10
Cлайд 4
Cлайд 5
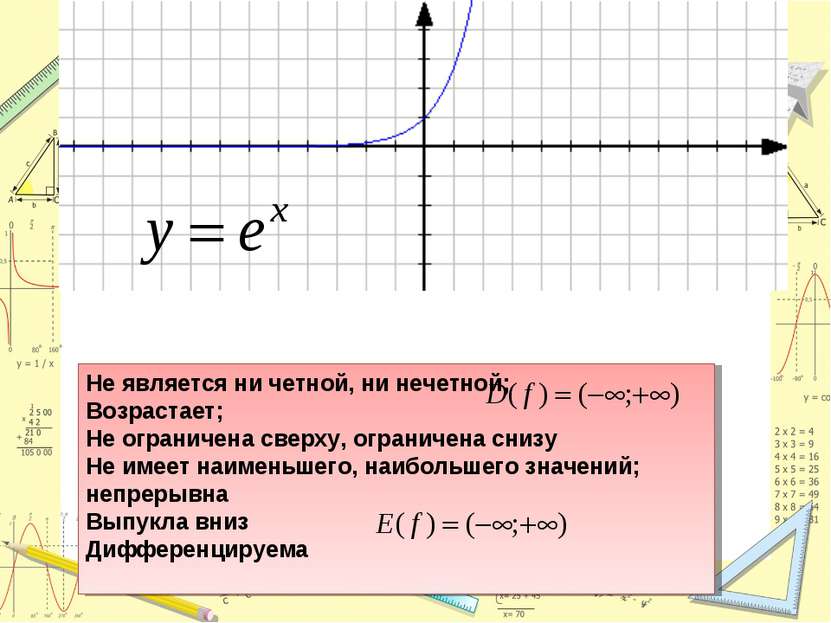
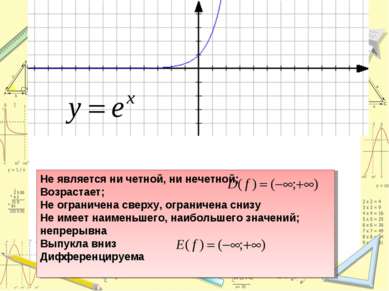Не является ни четной, ни нечетной; Возрастает; Не ограничена сверху, ограничена снизу Не имеет наименьшего, наибольшего значений; непрерывна Выпукла вниз Дифференцируема
Cлайд 6
Функция Производная
Cлайд 7
-ctg x tg x cos x -sin x sin x cos x y= f(kx+b) y=f(x)+g(x) Y=F(x)+G(x) y=kf(x) Y=kF(x)
Cлайд 8
=F(b) – F(a).
Cлайд 9
Cлайд 10
Логарифм по основанию е называется натуральным логарифмом Десятичные логарифмы для наших потребностей являются весьма удобными. Однако при изучении высшей математики более удобными оказываются логарифмы по основанию е = 2,718281828... (см. § 134, ч. 1). Употребление этих логарифмов позволяет значительно упростить большое количество математических формул. Логарифмы по основанию е получаются при решении многих физических задач и естественным образом входят в математическое описание некоторых химических, биологических и других процессов. Этим и объясняется их название «натуральные логарифмы». Натуральный логарифм числа а обозначается ln а. Сейчас имеются достаточно полные таблицы натуральных логарифмов.
Cлайд 11
Cлайд 12
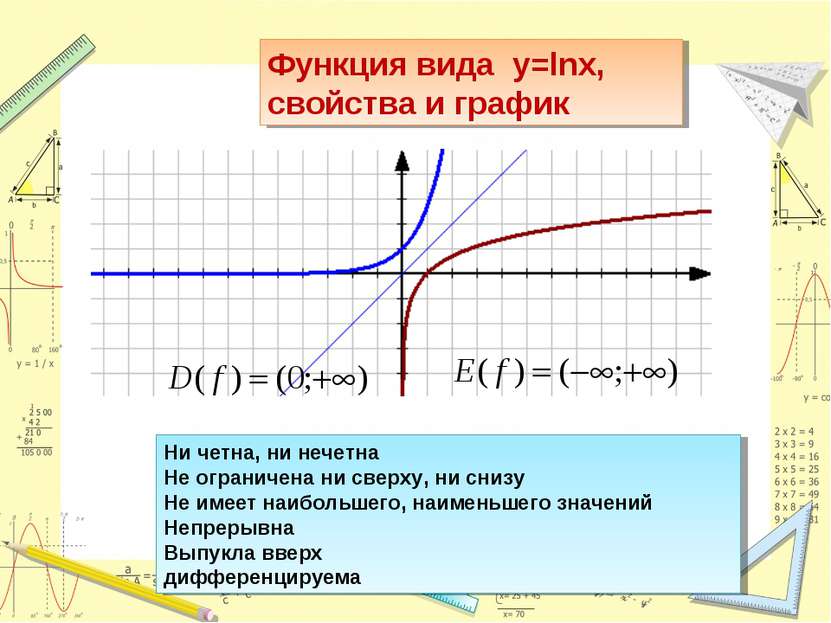
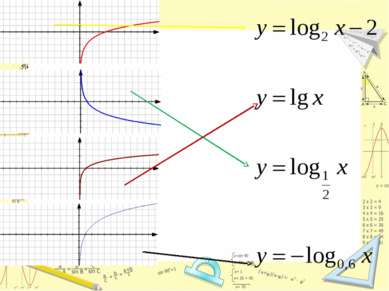
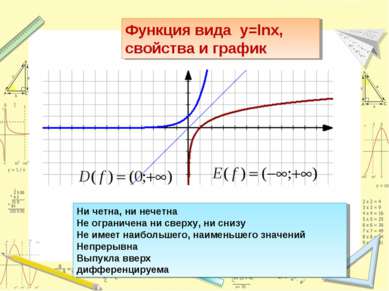Функция вида y=lnx, свойства и график Ни четна, ни нечетна Не ограничена ни сверху, ни снизу Не имеет наибольшего, наименьшего значений Непрерывна Выпукла вверх дифференцируема
Cлайд 13
Cлайд 14
1633, 1634, 1635, 1636(а,б) Дома: в,г
Cлайд 15
№1633
Cлайд 16
№1634
Cлайд 17
№1635
Cлайд 18
№1636
Cлайд 19
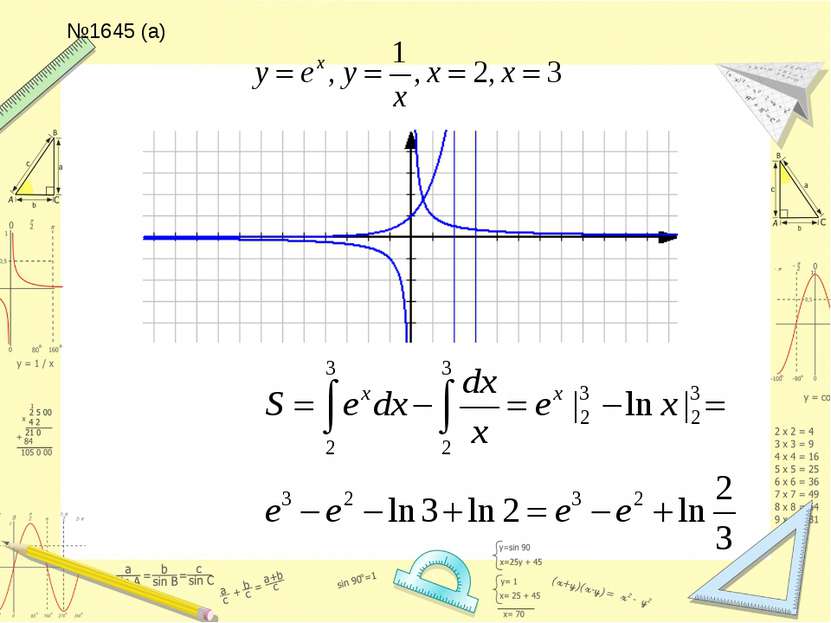
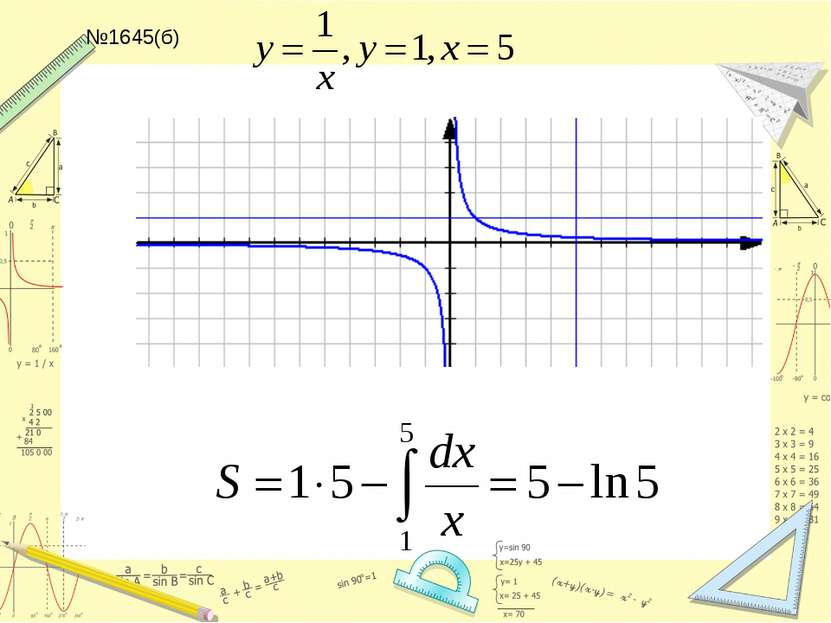
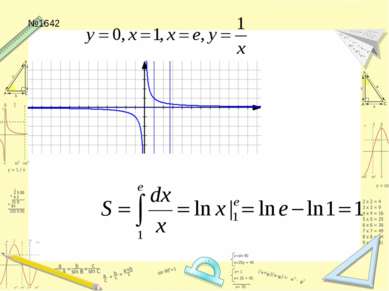
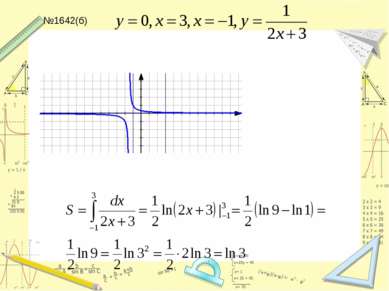
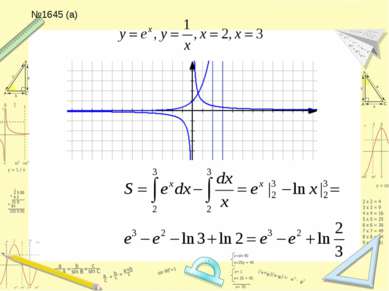
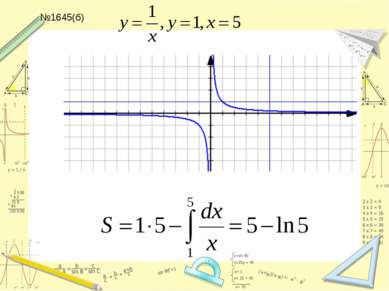
Составить уравнение касательной к графику функции y=lnx в точке x=e №1623,1637,1641 (а,б) в,г - дома
Cлайд 20
№1642, 1643
Cлайд 21
Вычислить площадь фигуры, ограниченной прямыми y=0, x=1, x=e и гиперболой
Cлайд 22
№1628, 1629, 1642, 1645 (а,б) дома: в,г
Cлайд 23
№1629 (а)
Cлайд 24
№1629(б)
Cлайд 25
№1642
Cлайд 26
№1642(б)
Cлайд 27
№1645 (а)
Cлайд 28
№1645(б)
Cлайд 29
Задание на каникулы: Создать справочник по формулам (лучше напечатать, чтобы можно было размножить), презентация, видеоролик и т.п. Тригонометрические формулы Тригонометрические уравнения (общий вид, частные случаи, методы решения) Производная Применение производной к исследованию функций Функции, свойства, графики, преобразования Первообразная и интеграл Показательные уравнения и неравенства Логарифмические уравнения и неравенства Степени и корни Системы уравнений Основные типы задач РЕШАТЬ ВАРИАНТЫ ЕГЭ
