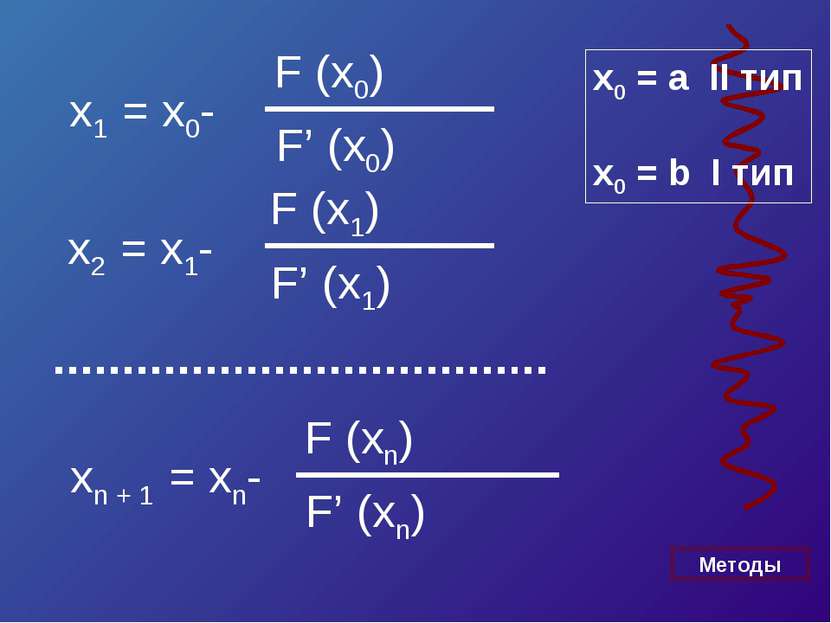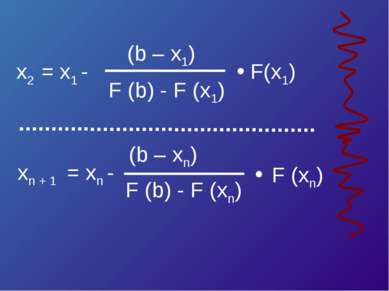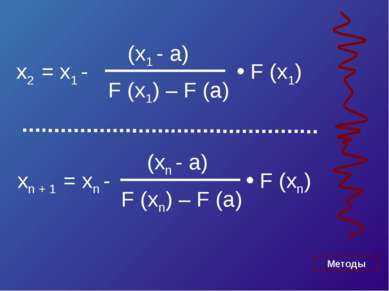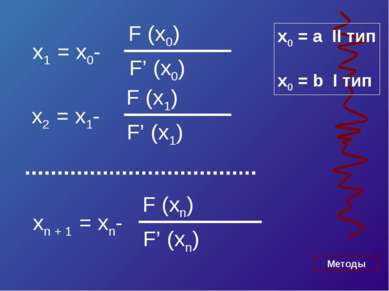X
Код презентации скопируйте его
Численные методы решения уравнений
Скачать эту презентациюПрезентация на тему Численные методы решения уравнений
Скачать эту презентациюCлайд 3
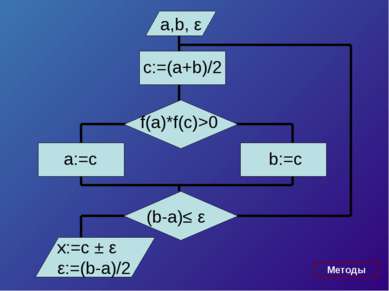
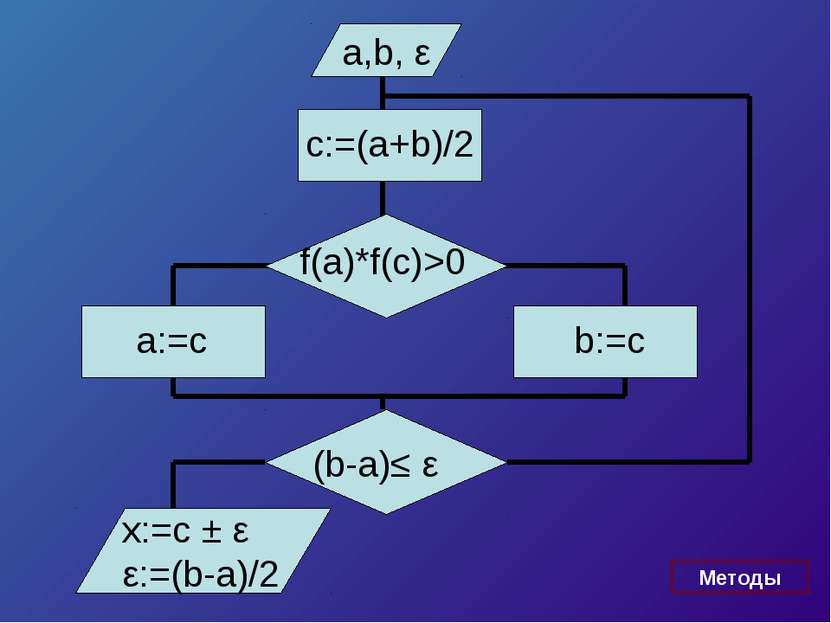
![Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a > ε Бу... Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a > ε Бу...](https://bigslide.ru/images/15/14227/389/img2.jpg) Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a > ε Будем считать, что функция: 1)Непрерывна и монотонна на отрезке [a, b] 2)f (a) x f (b) < 0 Итак разделим отрезок [a, b] пополам, середина отрезка c = (a + b) / 2 Отрезок [a, b] разделен на два отрезка [a, c] и [c, b], длина каждого = (b – a) / 2
Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a > ε Будем считать, что функция: 1)Непрерывна и монотонна на отрезке [a, b] 2)f (a) x f (b) < 0 Итак разделим отрезок [a, b] пополам, середина отрезка c = (a + b) / 2 Отрезок [a, b] разделен на два отрезка [a, c] и [c, b], длина каждого = (b – a) / 2
Cлайд 4
![x y a b c C = (a + b) / 2 a1 b1 c1 a2 b2 c2 b-a>ε [a; c] и [c; b], длина отре... x y a b c C = (a + b) / 2 a1 b1 c1 a2 b2 c2 b-a>ε [a; c] и [c; b], длина отре...](https://bigslide.ru/images/15/14227/389/img3.jpg) x y a b c C = (a + b) / 2 a1 b1 c1 a2 b2 c2 b-a>ε [a; c] и [c; b], длина отрезков (b - a) / 2 [an; bn ], длина (b-a)/2n (b-a)/2n
x y a b c C = (a + b) / 2 a1 b1 c1 a2 b2 c2 b-a>ε [a; c] и [c; b], длина отрезков (b - a) / 2 [an; bn ], длина (b-a)/2n (b-a)/2n
Cлайд 7
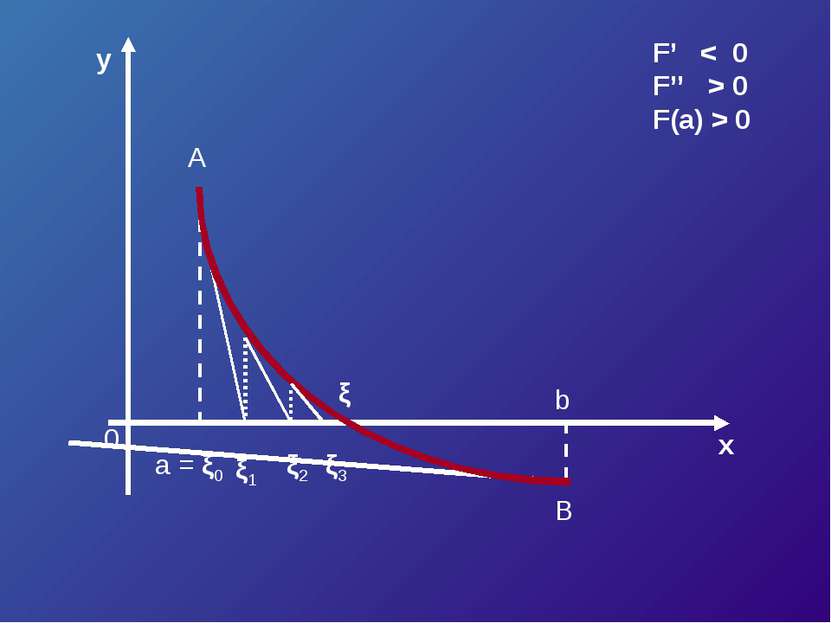
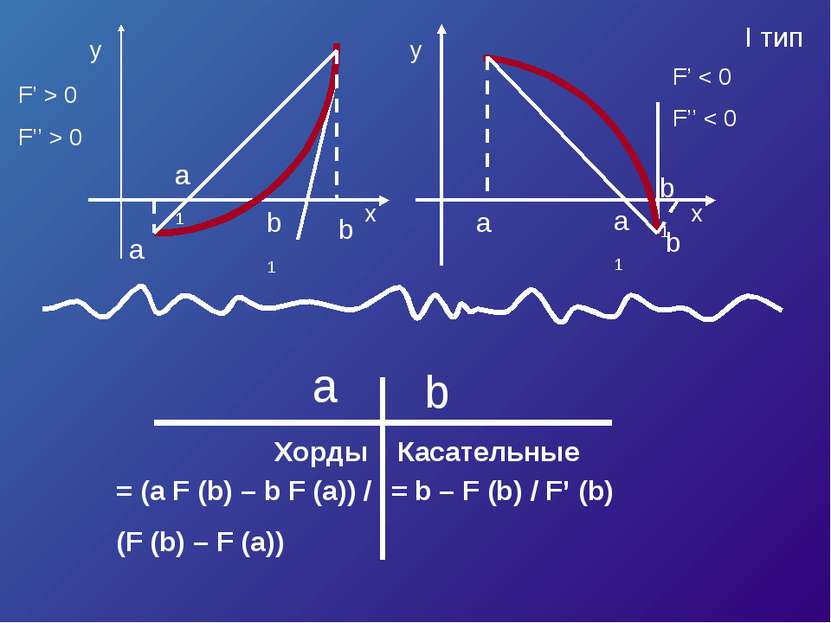
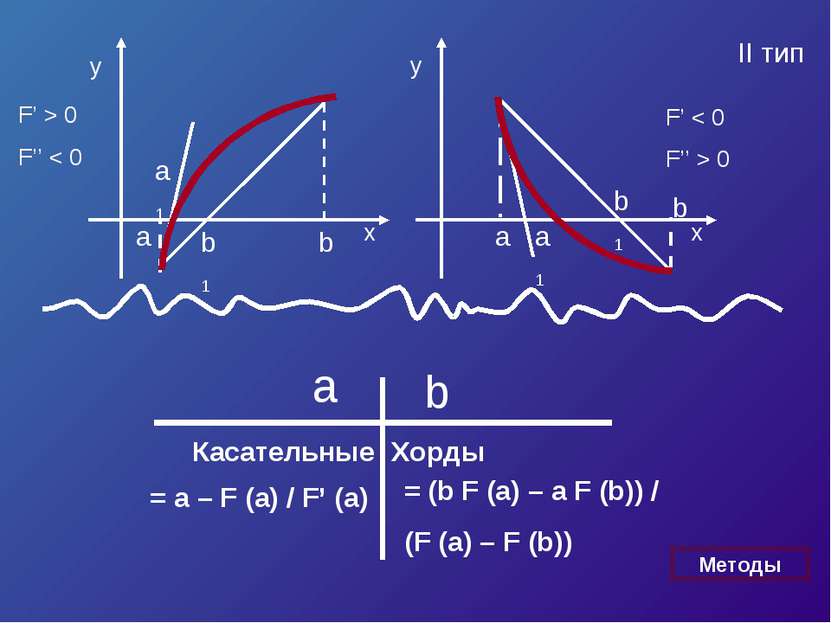
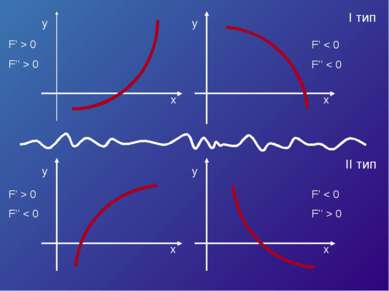
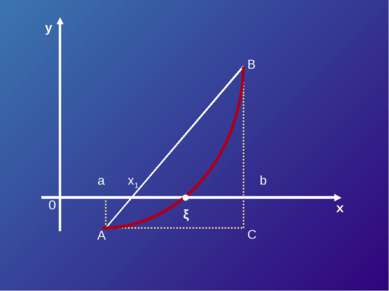
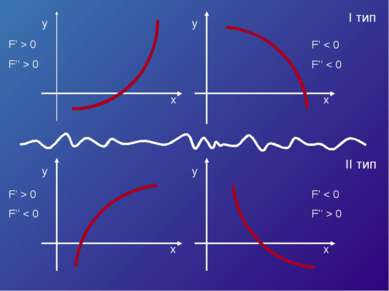
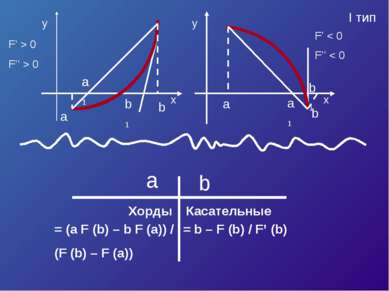
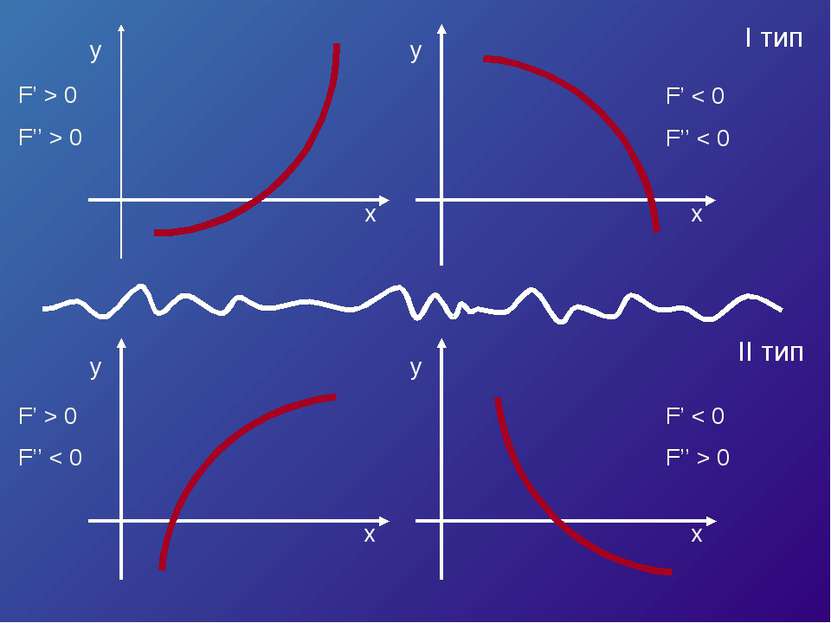
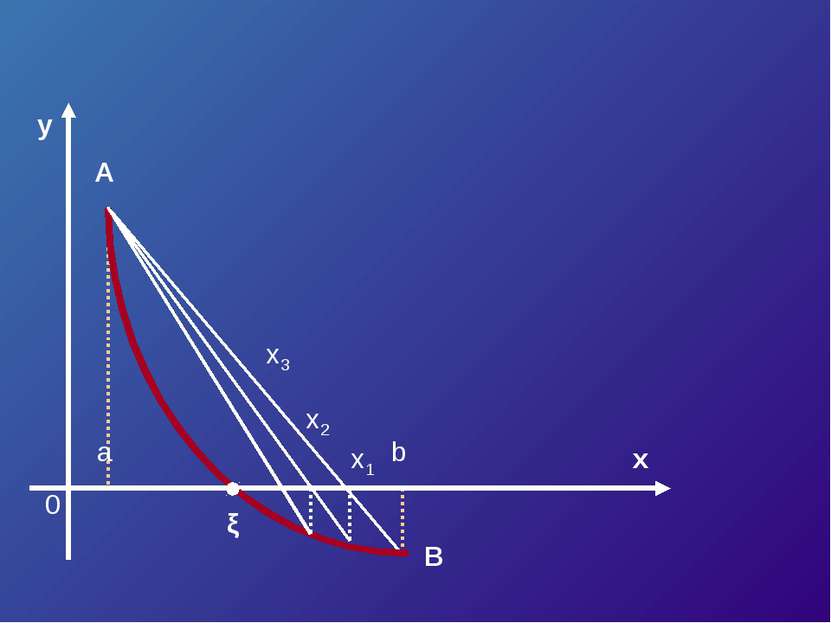
![Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: F ... Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: F ...](https://bigslide.ru/images/15/14227/389/img6.jpg) Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: F (x) непрерывна на отрезке [a; b] F (x) имеет на данном отрезке производные первого и второго порядков, производные сохраняют знак. F (a) * F (b) < 0
Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: F (x) непрерывна на отрезке [a; b] F (x) имеет на данном отрезке производные первого и второго порядков, производные сохраняют знак. F (a) * F (b) < 0
Cлайд 16
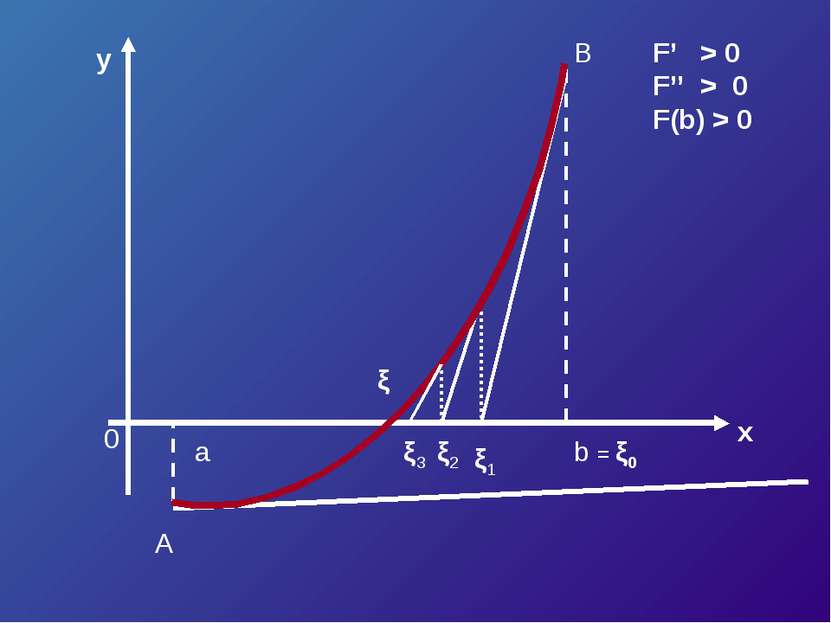
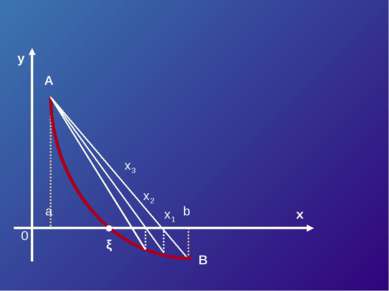
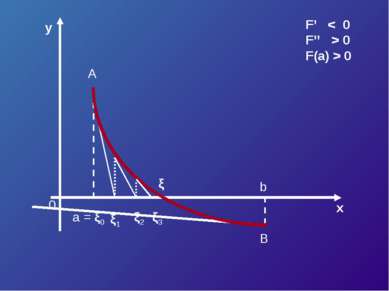
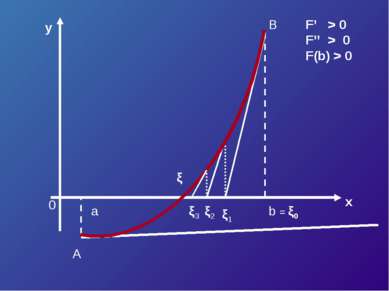
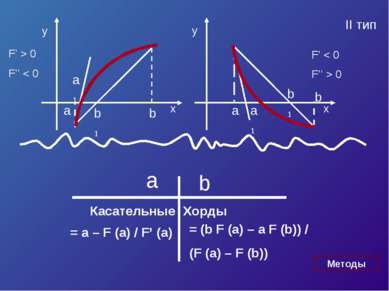
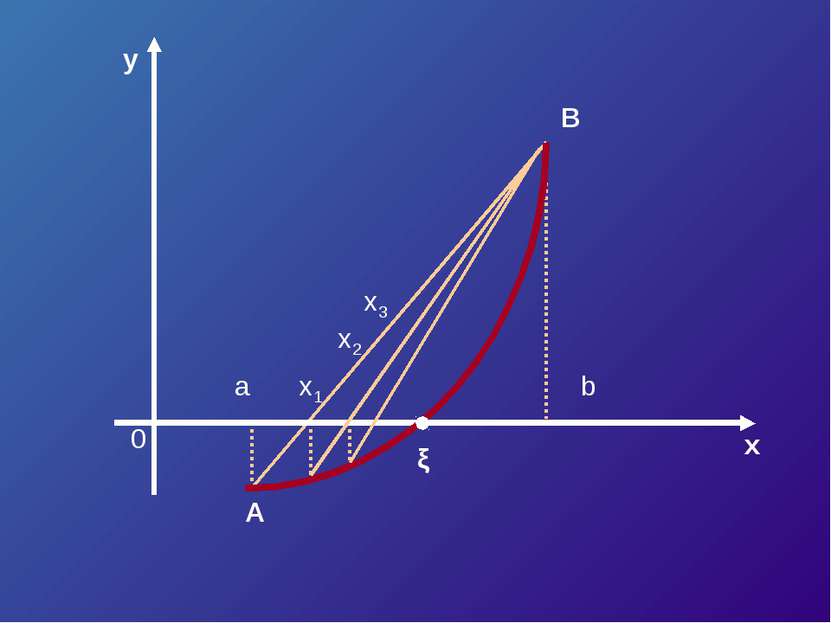
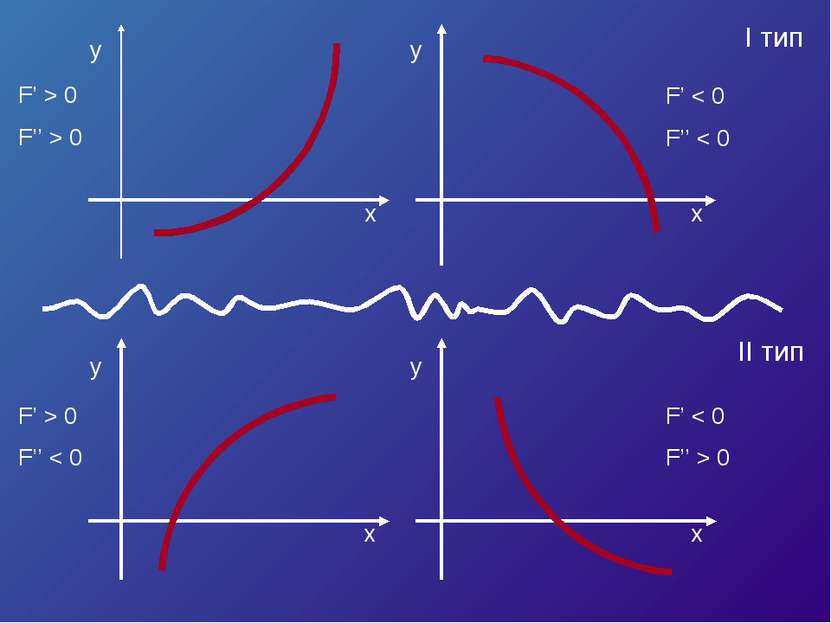
![Пусть корень ξ уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: ... Пусть корень ξ уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: ...](https://bigslide.ru/images/15/14227/389/img15.jpg) Пусть корень ξ уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: F (x) непрерывна на отрезке [a; b] F (x) имеет на данном отрезке производные первого и второго порядков, производные сохраняют знак. F (a) * F (b) < 0
Пусть корень ξ уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: F (x) непрерывна на отрезке [a; b] F (x) имеет на данном отрезке производные первого и второго порядков, производные сохраняют знак. F (a) * F (b) < 0
Cлайд 18
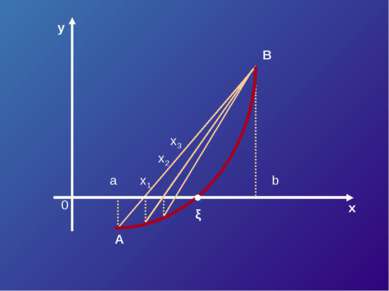
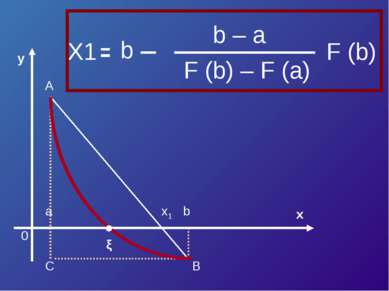
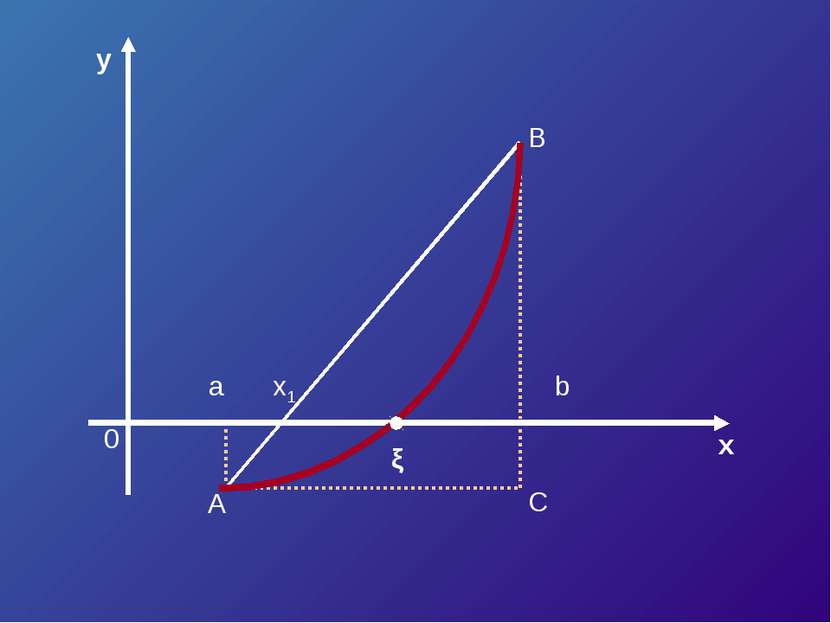
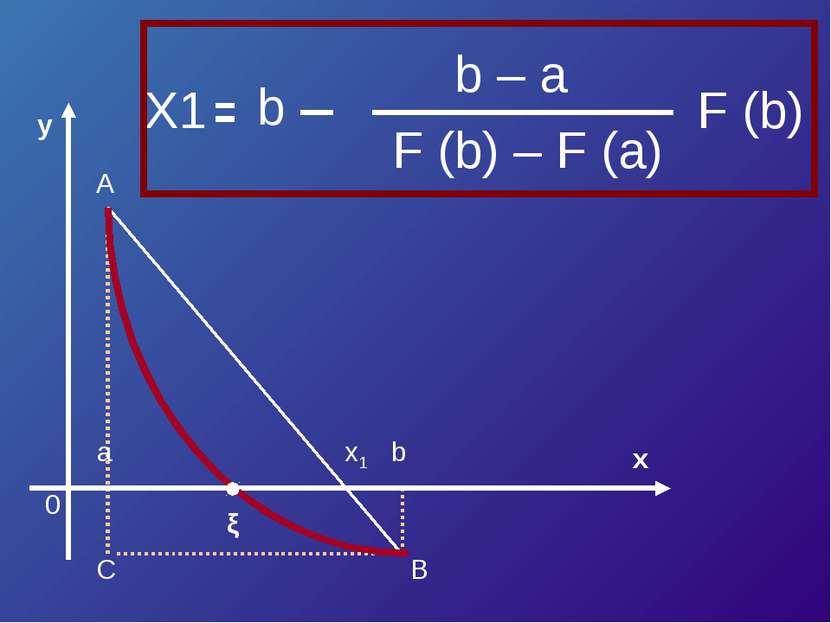
 Уравнение касательной в точке A (a, F (a)) : y – F (a) = F’ (a)*(x – a). Полагая y = 0, x = ξ 1 , получим
Уравнение касательной в точке A (a, F (a)) : y – F (a) = F’ (a)*(x – a). Полагая y = 0, x = ξ 1 , получим



![Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a > ε Бу... Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a > ε Бу...](https://bigslide.ru/images/15/14227/831/img2.jpg)
![x y a b c C = (a + b) / 2 a1 b1 c1 a2 b2 c2 b-a>ε [a; c] и [c; b], длина отре... x y a b c C = (a + b) / 2 a1 b1 c1 a2 b2 c2 b-a>ε [a; c] и [c; b], длина отре...](https://bigslide.ru/images/15/14227/831/img3.jpg)
![Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: F ... Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: F ...](https://bigslide.ru/images/15/14227/831/img6.jpg)

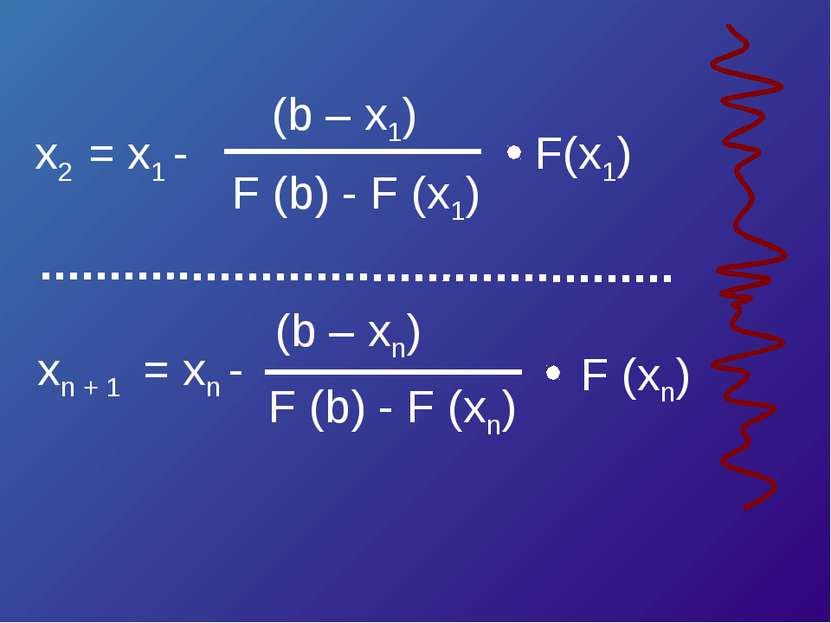
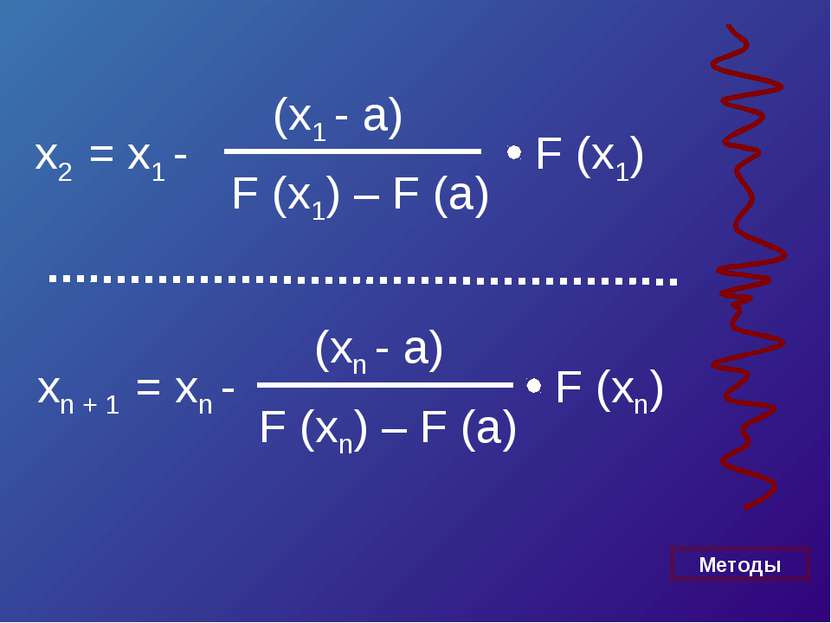
![Пусть корень ξ уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: ... Пусть корень ξ уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: ...](https://bigslide.ru/images/15/14227/831/img15.jpg)