X
Код презентации скопируйте его
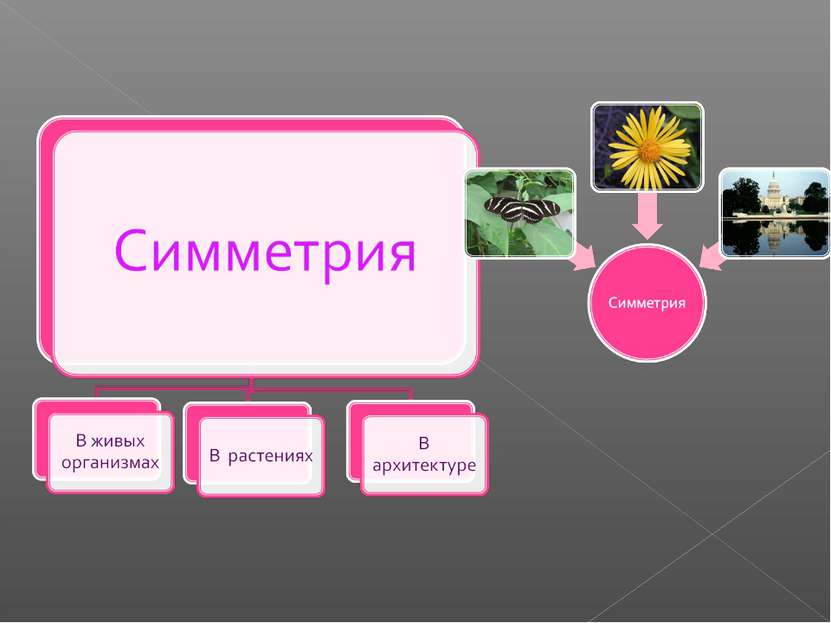
Симметрия везде
Скачать эту презентацию
Презентация на тему Симметрия везде
Скачать эту презентациюCлайд 1
Cлайд 2
Cлайд 3
В японском городе Никко есть ворота, которые японцы называют самыми красивыми воротами страны. Они были построены в период большого влияния китайского искусства. Это необычайно сложные ворота, со множеством фронтонов, изумительной резьбой и большим количеством колонн, на основании которых вырезаны драконьи головы, божества... Но, приглядевшись, можно заметить, что в сложном и искусном рисунке на одной из колонн некоторые из его мелких деталей вырезаны вверх ногами. В остальном рисунок полностью симметричен. Спрашивается: для чего это было нужно? Как говорит предание, это было сделано для того, чтобы боги не заподозрили человека в совершенстве. Ошибка была сделана намеренно, дабы не вызвать зависти и гнева богов. Ричард Фрейнман
Cлайд 4
Что такое симметрия? Какие виды симметрии существуют? Чем осевая симметрия отличается от центральной? Где можно видеть симметричные объекты?
Cлайд 5
Ответственность и адаптивность Коммуникативные умения Творчество и любознательность Критическое и системное мышление Умения работать с информацией и медиасредствами Межличностное взаимодействие и сотрудничество Умения ставить и решать проблемы Направленность на саморазвитие Социальная ответственность
Cлайд 6
Cлайд 7
Как устроен мир?
Cлайд 8
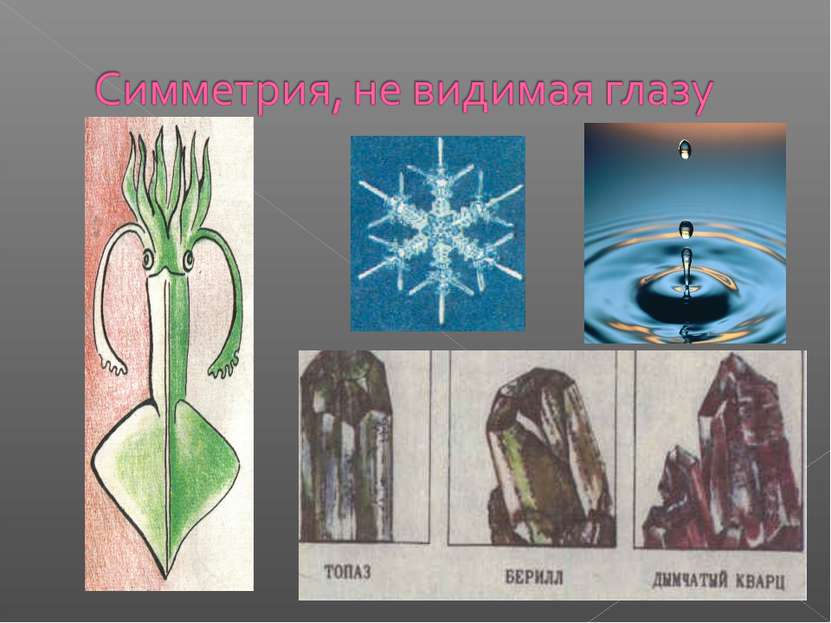
Есть ли полная симметрия в мире? Что дает симметрия? Возможен ли мир без симметрии? Почему в мире нет двух симметричных бабочек?
Cлайд 9
Cлайд 10
Для начала необходимо рассчитаться по порядку. Поскольку исследуем три темы, то и группы будет три. 1 группа – ботаники. Все , у кого число кратное трем(делится на три) 2 группа – зоологи. Все, у кого число при делении на три дает в остатке 1 3 группа – архитекторы. Все. У кого число при делении на три дает в остатке 2
Cлайд 11
Cлайд 12
Cлайд 13
