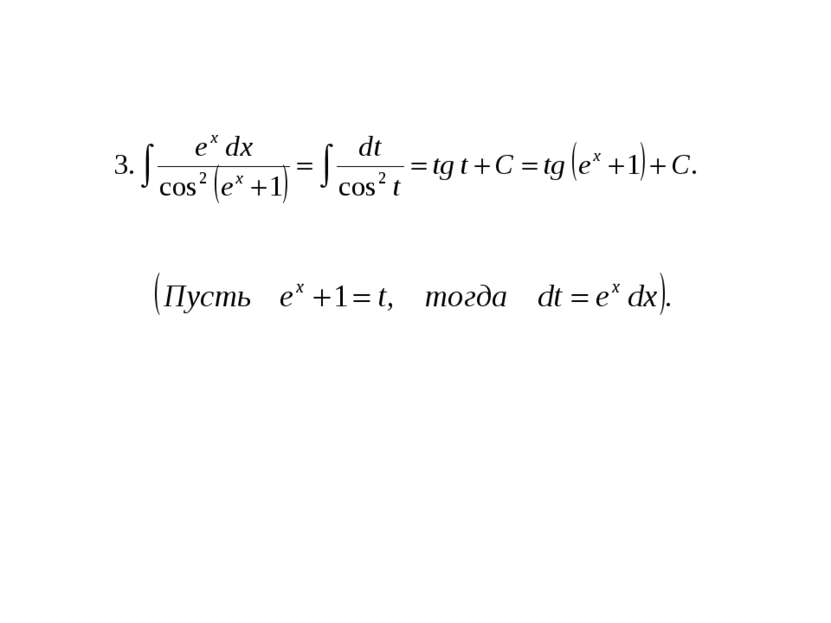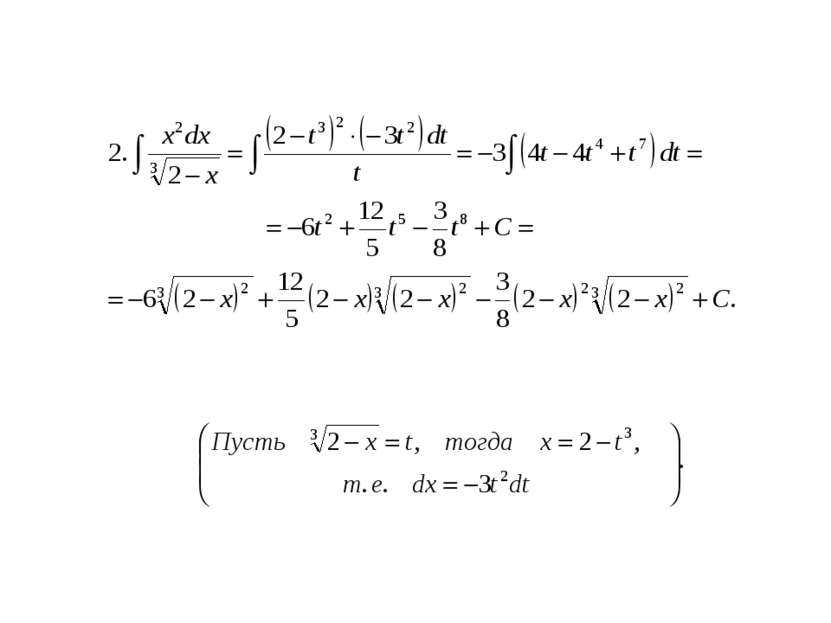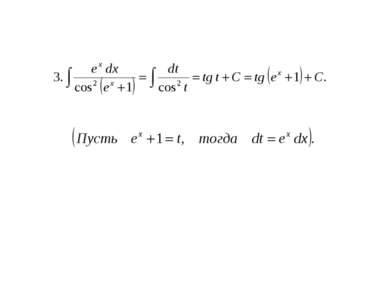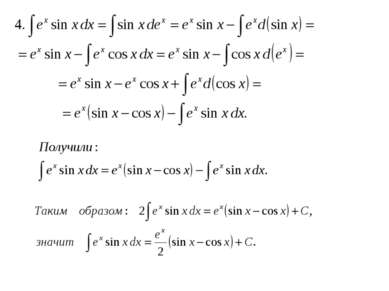X
Код презентации скопируйте его
Первообразная и неопределенный интеграл
Скачать эту презентацию
Презентация на тему Первообразная и неопределенный интеграл
Скачать эту презентациюCлайд 1
Первообразная и неопределенный интеграл Курышова Н.Е. лицей 488 Санкт-Петербург
Cлайд 2
Определение: Функция F(х) называется первообразной функции f(х) на промежутке Х, если Теорема: Если функция f(х) непрерывна при ,то для f(х) существует первообразная F(х) на Х. Замечание 1: Условие непрерывности не является необходимым для существования первообразной. Пример разрывной функции, имеющей первообразную:
Cлайд 3
Пример: Решение. Данная функция может быть записана в виде:
Cлайд 4
Замечание 2: Если функция f(х) определена на промежутке Х и в точке имеет разрыв в виде скачка, то есть , то функция f(x) не имеет первообразной на любом промежутке, содержащем точку . Теорема 2: Если F(x) одна из первообразных функции f(x), на промежутке Х, то любая первообразная на этом промежутке имеет вид F(x)+C. Определение: Множество всех первообразных функции f(x) называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается
Cлайд 5
Основные свойства неопределенного интеграла.
Cлайд 6
Основные методы Интегрирования.
Cлайд 7
Табличный. Сведение к табличному преобразованием подынтегрального выражения в сумму или разность. Интегрирование с помощью замены переменной (подстановкой). Интегрирование по частям.
Cлайд 8
Нахождение интеграла методом преобразования подынтегральной функции в сумму или разность.
Cлайд 9
Интегрирование методом замены переменной.
Cлайд 10
Cлайд 11
Интегрирование выражений, содержащих радикалы, методом подстановки.
Cлайд 12
Cлайд 13
Интегрирование алгебраических дробей.
Cлайд 14
Интегрирование по частям.
Cлайд 15
Cлайд 16
Используемая литература: Л.И.Звавич; А.Р. Рязановский; А.М.Поташник «Сборник задач по алгебре и математическому анализу для 10-11 классов» (учебное пособие для учащихся школ и классов с углубленным изучением математики.Москва Новая школа, 1996. Н.Я. Виленкин; О.С. Ивашев-Мусатов; С.И. Шварцбург «Алгебра и математический анализ для 10 классов». М.:Просвещение, 1995. Н.Я. Виленкин; О.С. Ивашев-Мусатов; С.И. Шварцбург «Алгебра и математический анализ для 11 классов». М.:Просвещение, 1995.
