X
Код презентации скопируйте его
Методы решения уравнений третьей степени
Скачать эту презентацию
Презентация на тему Методы решения уравнений третьей степени
Скачать эту презентациюCлайд 1
Методы решения уравнений третьей степени. Простейший. Графический. Способ группировки (А, В, С) Метод подбора. Искусственный метод
Cлайд 2
1. Простейший метод A1. Решить уравнение х³ = 8 и выберите правильный ответ: -2; 2; 0; ; 2; - .
Cлайд 3
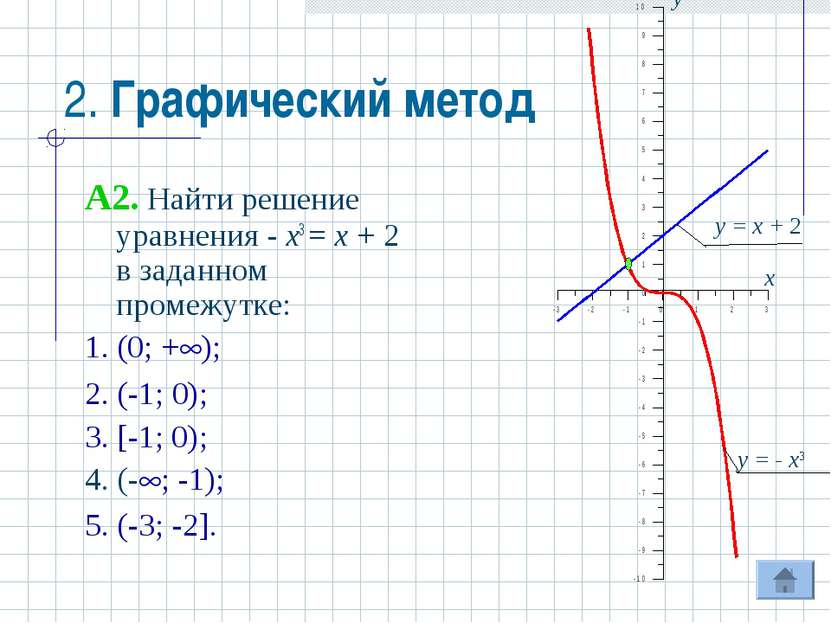
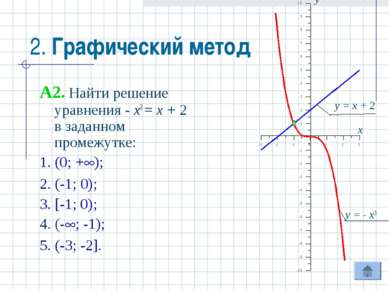2. Графический метод A2. Найти решение уравнения - x3 = x + 2 в заданном промежутке: 1. (0; + ); 2. (-1; 0); 3. [-1; 0); 4. (- ; -1); 5. (-3; -2].
Cлайд 4
3. Способ группировки А3. Среднее арифметическое всех корней уравнения х³ - 3х² - 4х + 12 = 0 равно 1) -1; 4) 2/3; 5) -3. 2) 1/3; 3) 1;
Cлайд 5
Решение: х³ - 3х² - 4х + 12 = 0 х² (х - 3) - 4(х - 3) = 0 (х - 3)(х² - 4) = 0 (х - 3)(х - 2)(х + 2) = 0 х = 3, х = 2, х = -2 (3+2+(-2))/3=1 Ответ:3 (записывают на листах ЕГЭ ответ)
Cлайд 6
Способ группировки В1. б) Найдите сумму корней уравнения х² + 6х + 5 = (х² - 1)(х + 3) Решение
Cлайд 7
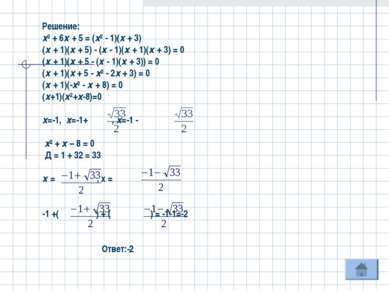Решение: х² + 6х + 5 = (х² - 1)(х + 3) (х + 1)(х + 5) - (х - 1)(х + 1)(х + 3) = 0 (х + 1)(х + 5 - (х - 1)(х + 3)) = 0 (х + 1)(х + 5 - х² - 2х + 3) = 0 (х + 1)(-х² - х + 8) = 0 (х+1)(х²+х-8)=0 х=-1, х=-1+ , х=-1 - х² + х – 8 = 0 Д = 1 + 32 = 33 х = , х = -1 +( ) + ( ) = -1-1=-2 Ответ:-2
Cлайд 8
Способ группировки в) Решение уравнений с модулем. Найдите наибольший корень уравнения |х - 2|х² = 18 - 9х ! обратить внимание х²: 18 - 9х ≥ 0, х ≤ 2. Решение
Cлайд 9
Решение: (-х + 2)х² = 18 - 9х -х³ + 2х² - 18х + 9х = 0 х²(-х + 2) - 9(2 - х) = 0 (2 - х)(х² - 9) = 0 х = 2, х = 3, х = -3 удовл.усл. не удовл.усл. удовл.усл. х≤2 х≤2 х≤2 Ответ: 2
Cлайд 10
4. Метод подбора. Решить уравнение: х³ - 3х² - 4х + 12 = 0 Решение
Cлайд 11
делители 12: ±1; 2;±3;±4;±6;±12 -1 не подходит +1 не подходит -2 подходит: (-8-12+8+12)=0 0=0(верно) х²-5х+6=0 х1=2, х2=3 Ответ: -2;2;3 х³-3х²4х+12|_х+2_ Решение x2-5x+6 х³+2х² -5х²-4х -5х²-10х 6х+12 6х+12 0
Cлайд 12
5. Искусственный метод А4. Если многочлен х³ + 2,5х² + 5х + 2 можно представить в виде (2х + 1)(ах² + bх + с), то сумма а+b+с равна 5) 5. 4) 3,5; 2) 2,5; 1) 4,5; 3) 3; Решение
Cлайд 13
Решение: х³ + 2,5х² + 5х + 2 = (2х + 1)(ах² + bх + с) х³+2,5х²+5х+2=2ах³+2bх²+2хс+ах²+bх+с 2а=1, а = = 0,5 а = 0,5 2,5=2b + а с = 2 5 = 2с+ b = 1 с = 2 а + b + с = 0,5 + 2 + 1 = 3,5 Ответ: 3,5
Cлайд 14
Молодец!
Cлайд 15
Подумай ещё! Этот ответ неверен
