X
Код презентации скопируйте его
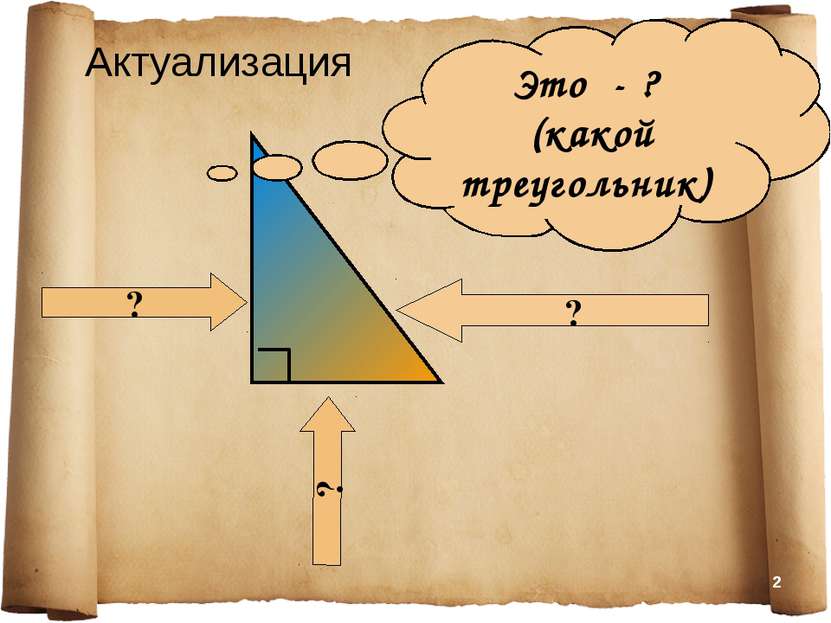
Установление соотношения между сторонами и углами прямоугольного треугольника
Скачать эту презентацию
Презентация на тему Установление соотношения между сторонами и углами прямоугольного треугольника
Скачать эту презентациюCлайд 1
п.53, выучить теорему Повторить теорию «Площади» обязательно №№480 (а, в); дополнительно 481 (выборочная проверка _ собрать тетради в конце урока) Домашнее задание *
Cлайд 2
? ? ? Это - ? (какой треугольник) * Актуализация
Cлайд 3
Практическая работа «Установление соотношения между сторонами и углами прямоугольного треугольника» Цель: провести исследование соотношения между катетами и гипотенузой в прямоугольном треугольнике Вывод: о соотношениях между катетами и гипотенузой (запишите в тетрадях) № измерения I катет II катет гипотенуза квадрат I катета квадрат II катета Сумма квадратов катетов > < = Квадрат гипотенузы 1 2 3
Cлайд 4
Теорема Пифагора *
Cлайд 5
Рефлексия Что нового вы узнали о прямоугольном треугольнике? На какие свойства площадей опирались при доказательстве теоремы Пифагора? Какие ранее изученные формулы площади мы использовали?
Cлайд 6
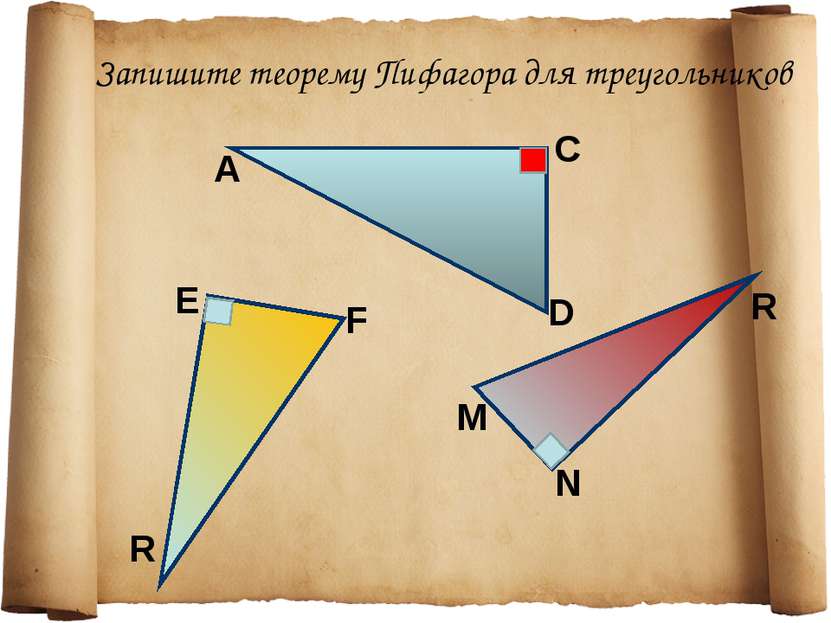
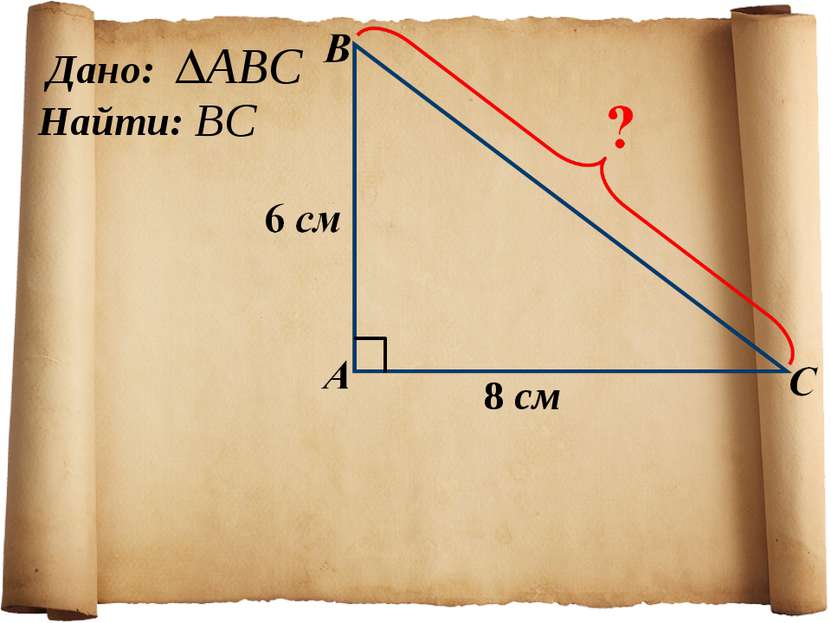
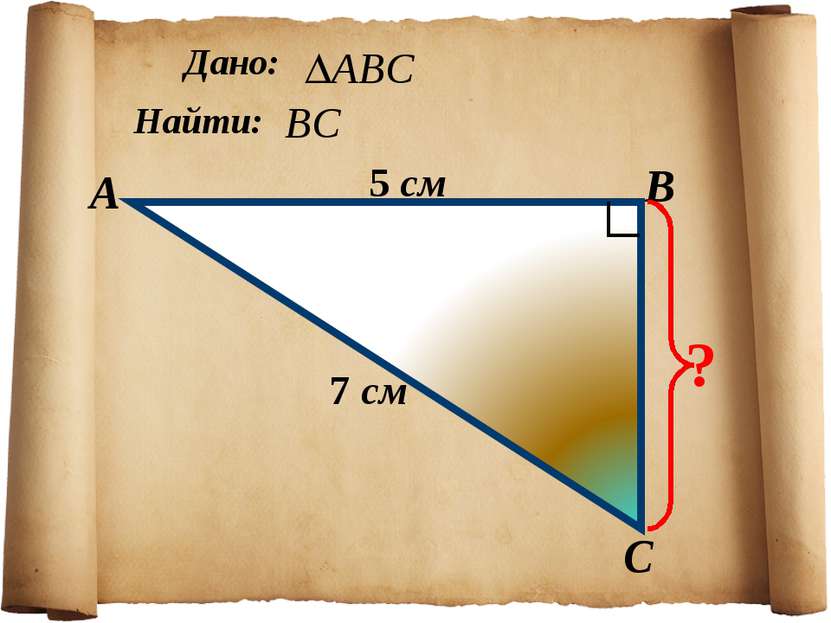
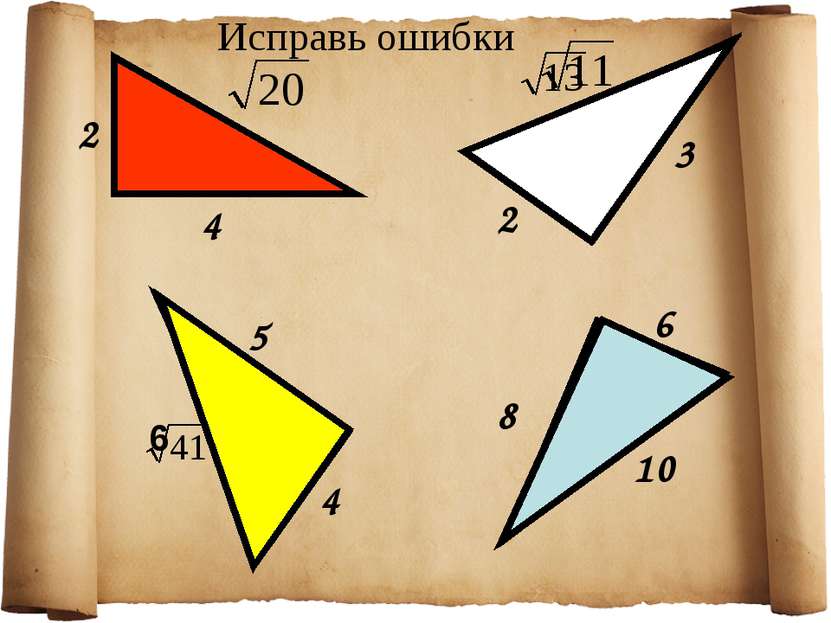
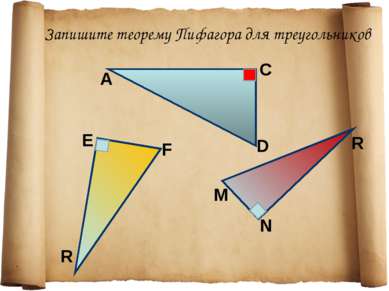
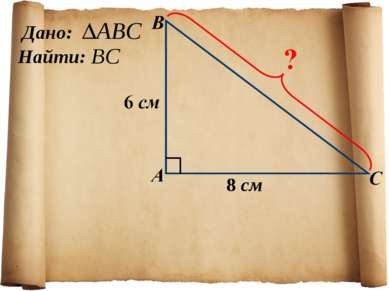
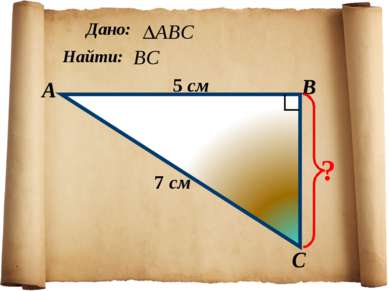
1. Указать прямоугольный треугольник 2. Записать для него теорему Пифагора с2 = а2+b2 Подставить известные значения сторон. Найти неизвестную сторону, произведя вычисления. Алгоритм применения теоремы Пифагора
Cлайд 7
Запишите теорему Пифагора для треугольников C D F E R M R N A
Cлайд 8
Найти: Дано: 8 см
Cлайд 9
Дано: Найти:
Cлайд 10
(ок. 580 – 500 г. до н.э.)
Cлайд 11
Cлайд 12
Cлайд 13
6 Исправь ошибки
Cлайд 14
Домашнее задание П 54, вопрос 7, стр 134 №№483(а, в), 484(а, б)_ обязательно № 513_ по желанию
Cлайд 15
Cлайд 16
Сертификат Настоящим подтверждается успешное усвоение учащимися 8 Г класса теоремы Пифагора в ходе урока геометрии *
Cлайд 17
Пребудет вечной истина, как скоро Ее познает слабый человек! И ныне теорема Пифагора Верна, как и в его далекий век. Обильно было жертвоприношенье Богам от Пифагора. Сто быков Он отдал на закланье и сожженье За света луч, пришедший с облаков. Поэтому всегда с тех самых пор, Чуть истина рождается на свет, Быки ревут, ее почуя, свету вслед. Они не в силах свету помешать , А могут лишь, закрыв глаза, дрожать От страха, что вселил в них Пифагор.
Cлайд 18
Пифагоровы тройки Прямоугольные треугольники с целочисленными сторонами называют египетскими, а тройки целых чисел, для которых выполняется соотношение, связывающее стороны прямоугольного треугольника, – пифагоровыми тройками.
Cлайд 19
Пифагоровы тройки Пифагоровы числа обладают рядом свойств Один из «катетов» должен быть кратным трём. Один из «катетов» должен быть кратным четырём. Одно из пифагоровых чисел должно быть кратно пяти. а 3 5 6 7 9 11 13 15 17 b 4 12 8 24 40 60 84 112 144 c 5 13 10 25 41 61 85 113 145
