X
Код презентации скопируйте его
Некоторые представления физики твердого тела
Скачать эту презентацию
Презентация на тему Некоторые представления физики твердого тела
Скачать эту презентациюCлайд 1
Отступление 1. (Короткий экскурс в физику твердого тела) Некоторые представления физики твердого тела Лекции по дисциплине «Основы анализа поверхности методами атомной физики» Профессор каф. общей физики ТПУ Н.Н. Никитенков.
Cлайд 2
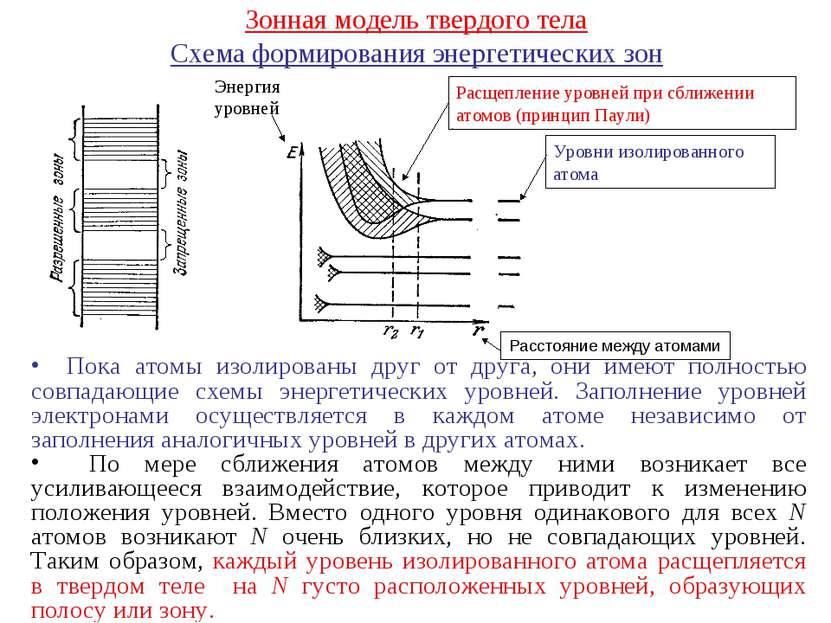
Зонная модель твердого тела Схема формирования энергетических зон Уровни изолированного атома Расщепление уровней при сближении атомов (принцип Паули) Пока атомы изолированы друг от друга, они имеют полностью совпадающие схемы энергетических уровней. Заполнение уровней электронами осуществляется в каждом атоме независимо от заполнения аналогичных уровней в других атомах. По мере сближения атомов между ними возникает все усиливающееся взаимодействие, которое приводит к изменению положения уровней. Вместо одного уровня одинакового для всех N атомов возникают N очень близких, но не совпадающих уровней. Таким образом, каждый уровень изолированного атома расщепляется в твердом теле на N густо расположенных уровней, образующих полосу или зону. Расстояние между атомами Энергия уровней
Cлайд 3
Зонная классификация твердых тел
Cлайд 4
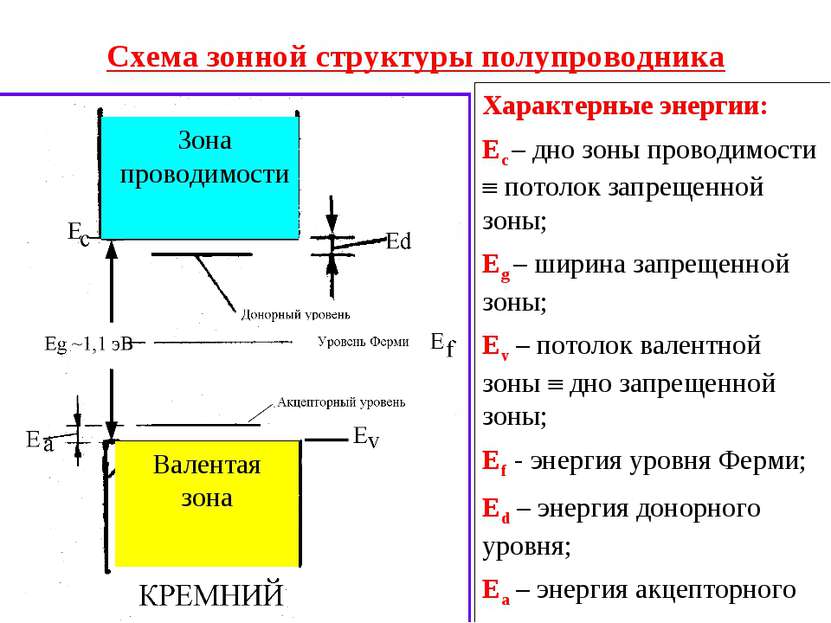
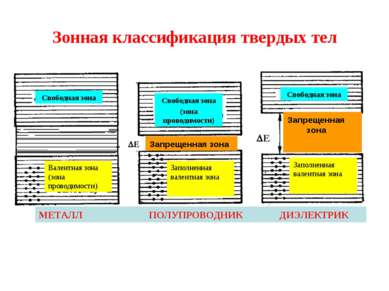
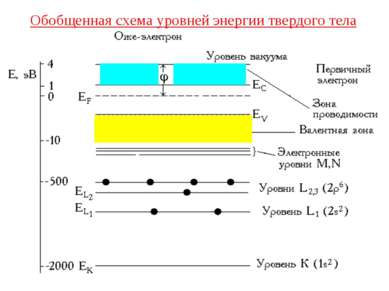
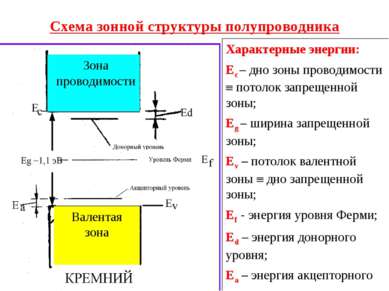Схема зонной структуры полупроводника Характерные энергии: Ес – дно зоны проводимости потолок запрещенной зоны; Еg – ширина запрещенной зоны; Еv – потолок валентной зоны дно запрещенной зоны; Еf - энергия уровня Ферми; Еd – энергия донорного уровня; Еа – энергия акцепторного уровня;
Cлайд 5
Обобщенная схема уровней энергии твердого тела
Cлайд 6
Распределение Ферми В применении к электронам квантовая механика считает электроны неразличимыми и чтобы в каждом состоянии системы не мог находиться более, чем один электрон. Исходя из этих требований функция распределения f электронов по энергетическим состояниям в твердом теле. Эта функция характеризует вероятность того, что данное энергетическое состояние занято и называется функцией распределения Ферми-Дирака; график ее изображен на рис. Энергия ЕF называется энергией Ферми. При абсолютном нуле (Т = 0°К) f = 1 при ЕEF. Таким образом, при абсолютном нуле ЕF имеет смысл предельной энергии; все состояния с энергией, меньшей ЕF, заняты, а все состояния с энергией, большей ЕF, вакантны.
Cлайд 7
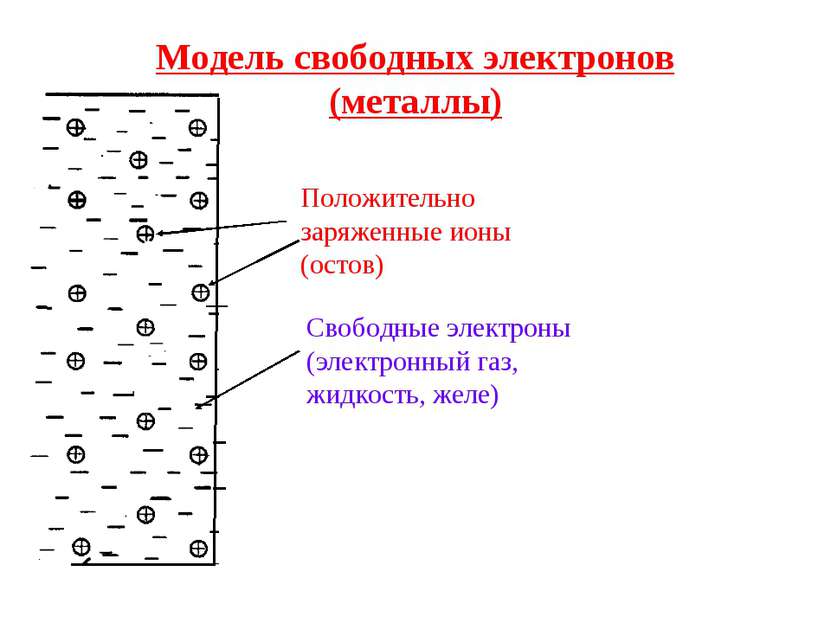
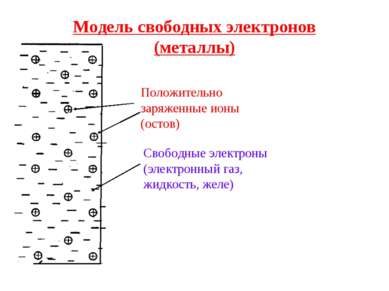Модель свободных электронов (металлы) Положительно заряженные ионы (остов) Свободные электроны (электронный газ, жидкость, желе)
Cлайд 8
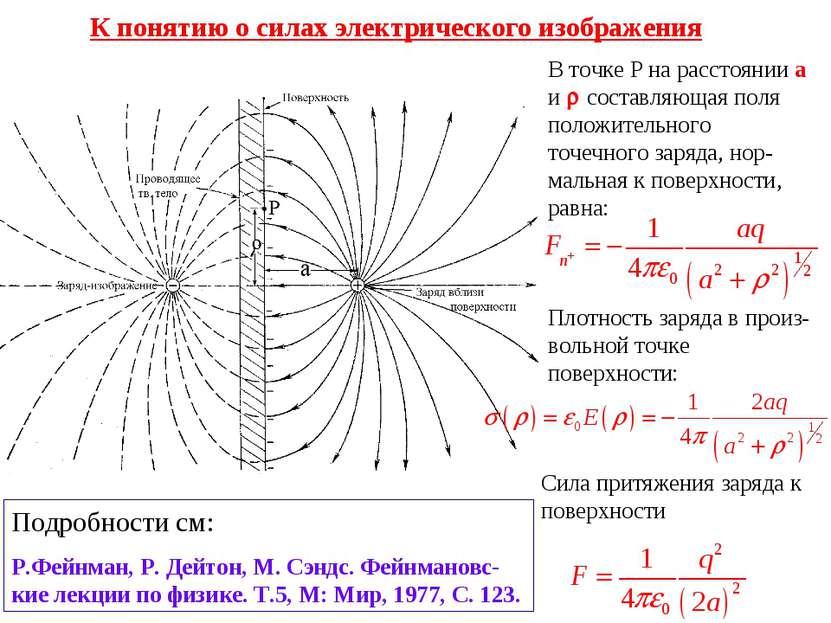
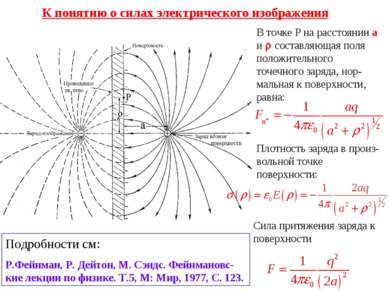К понятию о силах электрического изображения В точке Р на расстоянии а и составляющая поля положительного точечного заряда, нор-мальная к поверхности, равна: Плотность заряда в произ-вольной точке поверхности: Сила притяжения заряда к поверхности Подробности см: P.Фейнман, Р. Дейтон, М. Сэндс. Фейнмановс-кие лекции по физике. Т.5, М: Мир, 1977, С. 123.
Cлайд 9
Статистический вес в термодинамике и статистической физике - число способов, которыми может быть реализовано данное макроскопическое состояние системы. Термодинамически равновесное макроскопическое состояние системы характеризуется определенными значениями полной энергии, полного числа частиц N и объёма системы. Микроскопическое состояние системы соответствует заданному распределению её частиц по возможным классическим или квантовым состояниям. Статистический вес равен числу микроскопических состояний, которыми может быть реализовано данное макроскопическое состояние. Иногда Статистический вес называют термодинамической вероятностью.
