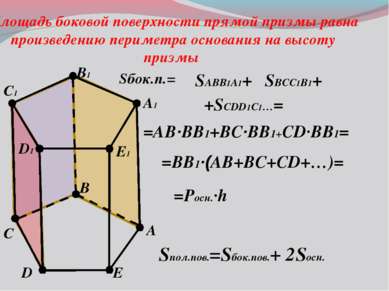
X
Код презентации скопируйте его
Пчелиные соты
Скачать эту презентациюПрезентация на тему Пчелиные соты
Скачать эту презентациюCлайд 6
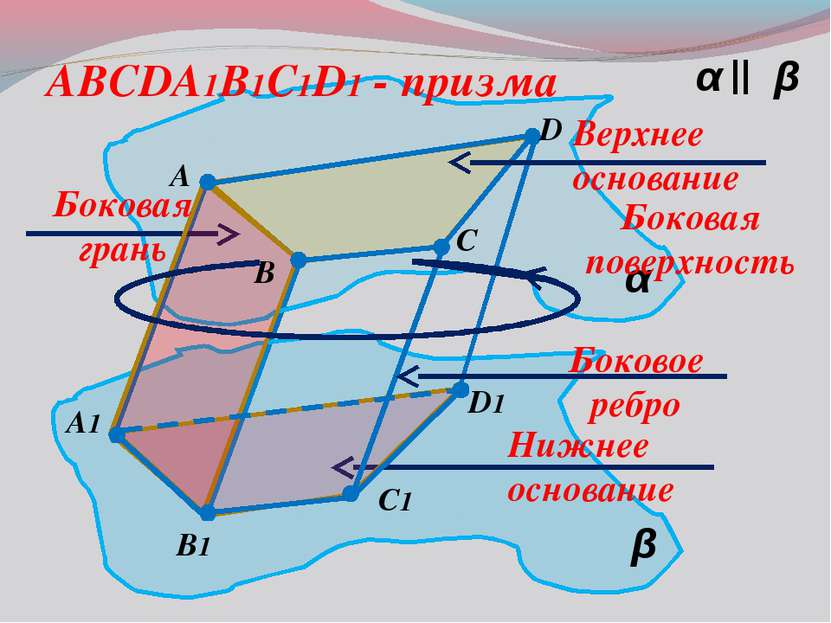
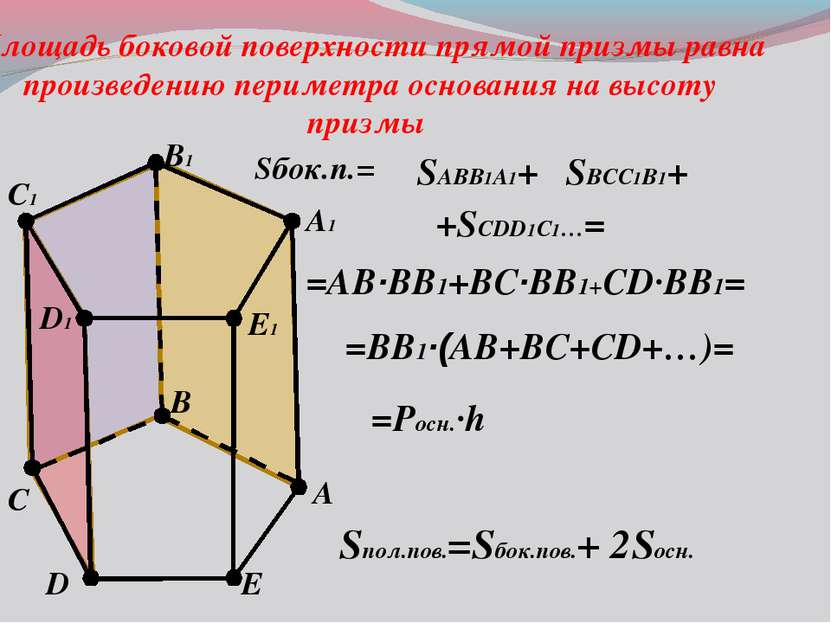
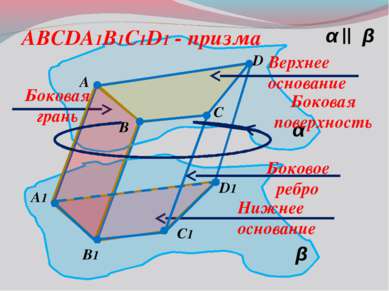 α β α β || A B C1 D A1 B1 D1 C ABCDA1B1C1D1 - призма Верхнее основание Нижнее основание Боковое ребро Боковая грань Боковая поверхность
α β α β || A B C1 D A1 B1 D1 C ABCDA1B1C1D1 - призма Верхнее основание Нижнее основание Боковое ребро Боковая грань Боковая поверхность
Cлайд 8
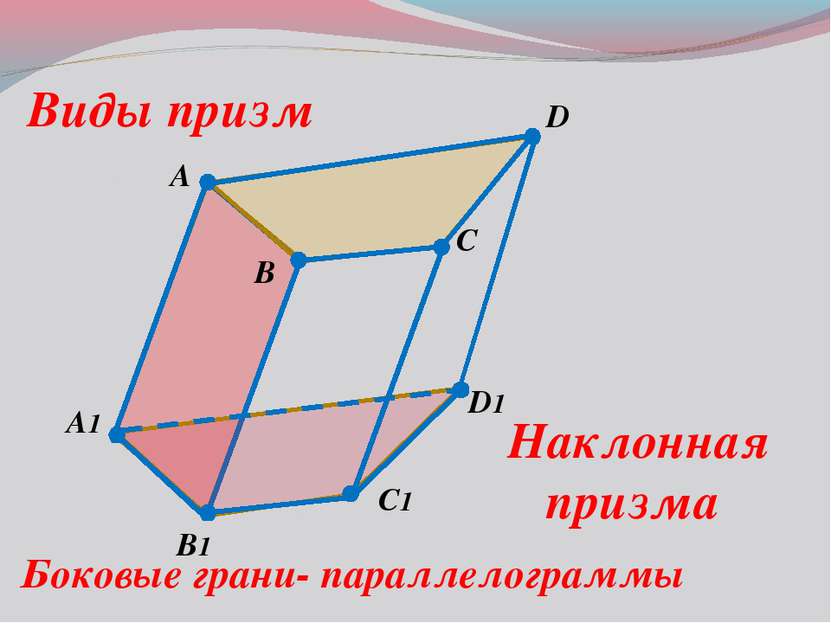
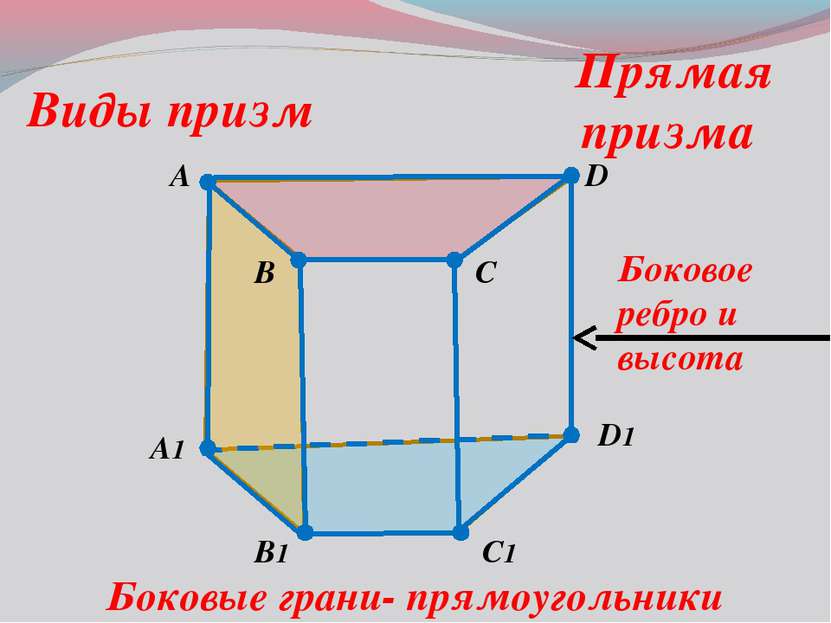
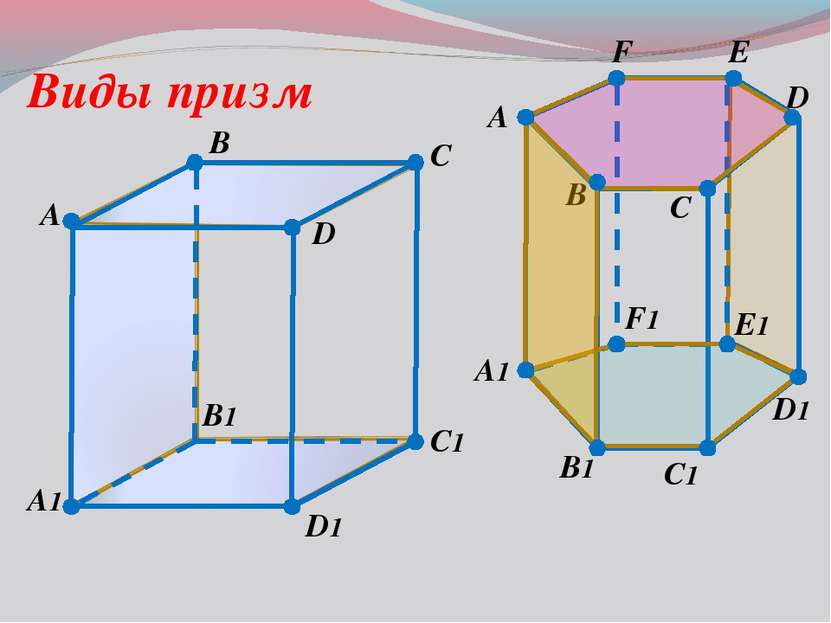
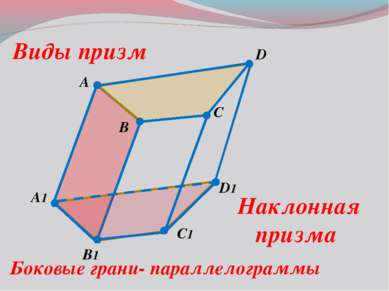
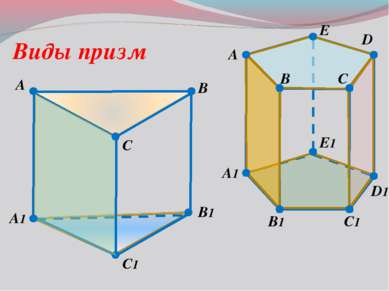
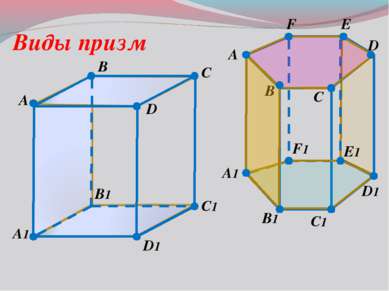
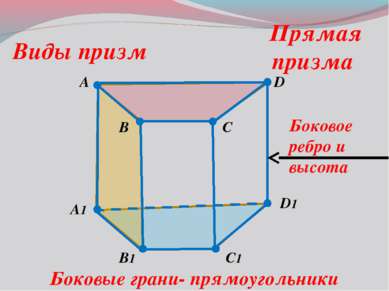 A B C1 D A1 B1 D1 C Виды призм Прямая призма Боковые грани- прямоугольники Боковое ребро и высота
A B C1 D A1 B1 D1 C Виды призм Прямая призма Боковые грани- прямоугольники Боковое ребро и высота
Cлайд 11
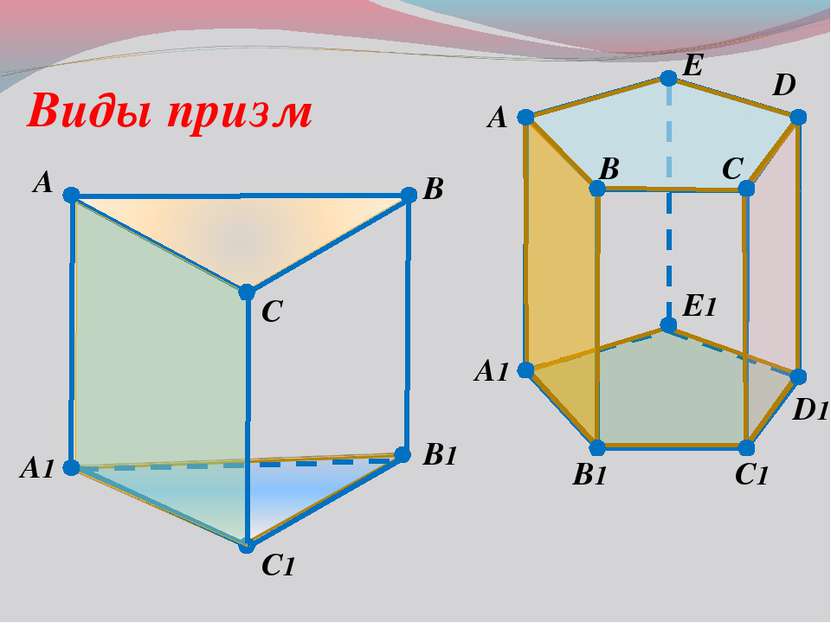
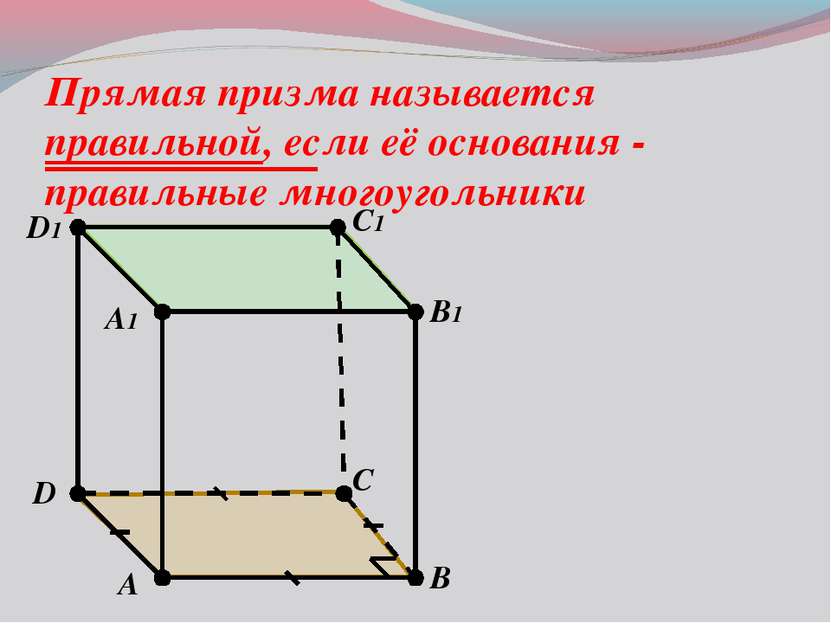
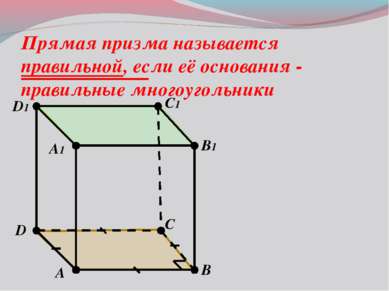 Прямая призма называется правильной, если её основания - правильные многоугольники B1 C1 D1 A1 A B C D
Прямая призма называется правильной, если её основания - правильные многоугольники B1 C1 D1 A1 A B C D