X
Код презентации скопируйте его
Некоторые применения теоремы Пифагора
Скачать эту презентациюПрезентация на тему Некоторые применения теоремы Пифагора
Скачать эту презентациюCлайд 2
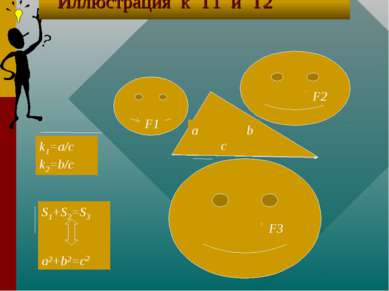
 Ниже будем использовать следующие обозначения: катеты и гипотенуза прямоугольного треугольника ABC соответственно a, b и c ; sin A = a / c, sin B = b / c ; фигуры 1, 2, 3, их длины, площади и их объемы соответственно F1,F2,F3;L1,L2,L3; S1,S2,S3 и V1,V2,V3.
Ниже будем использовать следующие обозначения: катеты и гипотенуза прямоугольного треугольника ABC соответственно a, b и c ; sin A = a / c, sin B = b / c ; фигуры 1, 2, 3, их длины, площади и их объемы соответственно F1,F2,F3;L1,L2,L3; S1,S2,S3 и V1,V2,V3.
Cлайд 3
 Теорема Пифагора и подобие фигур для n - мерного пространства Будем считать F1 подобной F2 в n - мерном пространстве с коэффициентом подобия к , если есть величины W1 и W2 соответственно такие, что W1/W2=kn. Т1. Если F1 подобна F3, где k=n V¯a2/c2, F2 подобна F3, где k= n V¯b2/c2, и W1+W2=W3, то a,b и с - стороны прямоугольного треугольника. Т2. Если F1 подобна F3, где k=n V¯a2/c2, F2 подобна F3, где k=n V¯ b2/c2, и а,b и с- стороны прямоугольного треугольника,то W1+W2 = W3.
Теорема Пифагора и подобие фигур для n - мерного пространства Будем считать F1 подобной F2 в n - мерном пространстве с коэффициентом подобия к , если есть величины W1 и W2 соответственно такие, что W1/W2=kn. Т1. Если F1 подобна F3, где k=n V¯a2/c2, F2 подобна F3, где k= n V¯b2/c2, и W1+W2=W3, то a,b и с - стороны прямоугольного треугольника. Т2. Если F1 подобна F3, где k=n V¯a2/c2, F2 подобна F3, где k=n V¯ b2/c2, и а,b и с- стороны прямоугольного треугольника,то W1+W2 = W3.
Cлайд 4
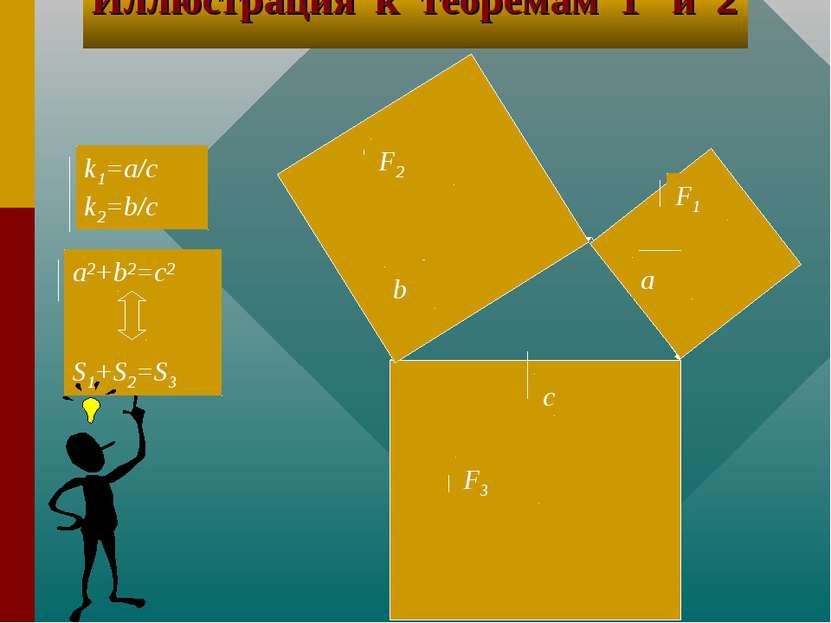
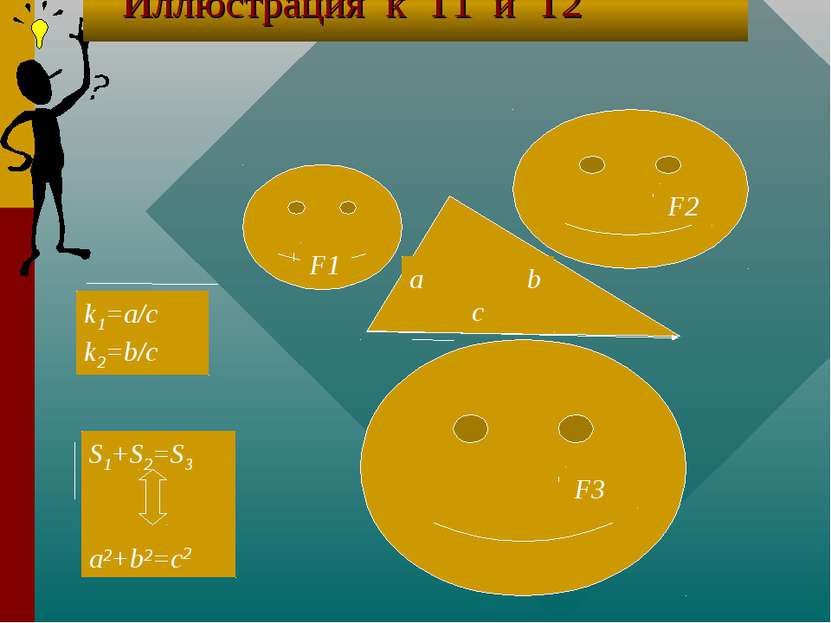
 Теорема 1 и теорема 2 для двухмерного пространства Т1. Если F1 подобна F3, где k=a/c=sin A, F2 подобна F3, где k=b/c=sin B, и S1+S2=S3 , то a,b и c- стороны прямоугольного треугольника. Т2. Если F1 подобна F3, где k=a/c=sin A, F2 подобна F3, где k=b/c=sin B, причем a, b и c- стороны прямоугольного треугольника, то S1+S2=S3.
Теорема 1 и теорема 2 для двухмерного пространства Т1. Если F1 подобна F3, где k=a/c=sin A, F2 подобна F3, где k=b/c=sin B, и S1+S2=S3 , то a,b и c- стороны прямоугольного треугольника. Т2. Если F1 подобна F3, где k=a/c=sin A, F2 подобна F3, где k=b/c=sin B, причем a, b и c- стороны прямоугольного треугольника, то S1+S2=S3.
Cлайд 6
 Доказательство Т 1 Из подобия фигур следует равенство : S1+S2 =S3(a2+b2)/c2 (см.доказательствоТ2). По условию S1+S2=S3 , следовательно (a2+b2)/c2=1 , откуда а2+b2=c2 . Тогда по обратной теореме Пифагора имеем : a, b и c есть стороны прямоугольного треугольника. Теорема доказана.
Доказательство Т 1 Из подобия фигур следует равенство : S1+S2 =S3(a2+b2)/c2 (см.доказательствоТ2). По условию S1+S2=S3 , следовательно (a2+b2)/c2=1 , откуда а2+b2=c2 . Тогда по обратной теореме Пифагора имеем : a, b и c есть стороны прямоугольного треугольника. Теорема доказана.
Cлайд 7
 Доказательство Т2 Из подобия фигур, отношение площадей которых равно квадрату коэффициента подобия, следует : S1= (a2/c2)S3 , S2= (b2/c2)S3. Тогда S1+S2= (a2/c2) S3+ (b2/c2)S3 = =(a2/c2+b2/c2)S3=S3(a2+b2)/c2=S3, так как по теореме Пифагора a2+b2=c2. Итак , имеем S1+S2=S3. Теорема доказана.
Доказательство Т2 Из подобия фигур, отношение площадей которых равно квадрату коэффициента подобия, следует : S1= (a2/c2)S3 , S2= (b2/c2)S3. Тогда S1+S2= (a2/c2) S3+ (b2/c2)S3 = =(a2/c2+b2/c2)S3=S3(a2+b2)/c2=S3, так как по теореме Пифагора a2+b2=c2. Итак , имеем S1+S2=S3. Теорема доказана.
Cлайд 9
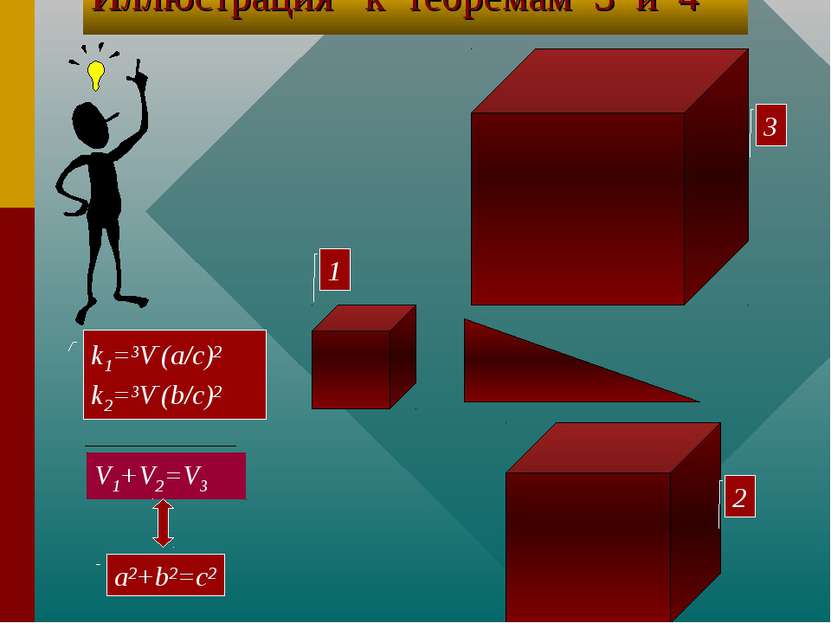
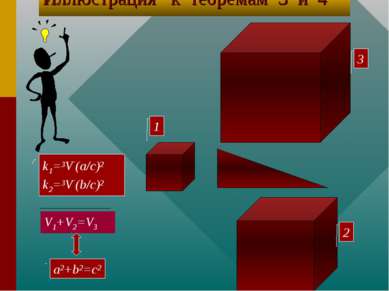
 Теорема 3 и теорема 4 для трехмерного пространства Т3. Если F1 подобна F3, где k=3V¯(a/c)2, F2 подобна F3 , где k=3V¯(b/c)2 , и V1+V2=V3 , то a,b и c- стороны прямоугольного треугольника. Т4. Если F1 подобна F3, где k=3V¯(a/c)2, F2 подобна F3 , где k=3V¯(b/c)2, причем a, b и c - стороны прямоугольного треугольника, то верно V1+V2=V3.
Теорема 3 и теорема 4 для трехмерного пространства Т3. Если F1 подобна F3, где k=3V¯(a/c)2, F2 подобна F3 , где k=3V¯(b/c)2 , и V1+V2=V3 , то a,b и c- стороны прямоугольного треугольника. Т4. Если F1 подобна F3, где k=3V¯(a/c)2, F2 подобна F3 , где k=3V¯(b/c)2, причем a, b и c - стороны прямоугольного треугольника, то верно V1+V2=V3.
Cлайд 10
 Доказательство Т3 и Т4. Отношение объемов подобных фигур равно кубу коэффициента подобия, поэтому V1=(а2/c2)V3 и V2=(b2/c2)V3 , откуда V1+V2=V3(a2+b2)/c2. (1) Т3.По условию V1+V2=V3 ,тогда из равенства(1) следует a2+b2=c2 и то,что a,b и c - cтороны прямоугольного треугольника. Т4. По условию a,b и c-стороны прямоугольного треугольника, т.е. a2+b2=c2,тогда из равенства (1) следует, что V1+V2=V3. Теоремы доказаны. Доказательство Т3 и Т4
Доказательство Т3 и Т4. Отношение объемов подобных фигур равно кубу коэффициента подобия, поэтому V1=(а2/c2)V3 и V2=(b2/c2)V3 , откуда V1+V2=V3(a2+b2)/c2. (1) Т3.По условию V1+V2=V3 ,тогда из равенства(1) следует a2+b2=c2 и то,что a,b и c - cтороны прямоугольного треугольника. Т4. По условию a,b и c-стороны прямоугольного треугольника, т.е. a2+b2=c2,тогда из равенства (1) следует, что V1+V2=V3. Теоремы доказаны. Доказательство Т3 и Т4
Cлайд 13
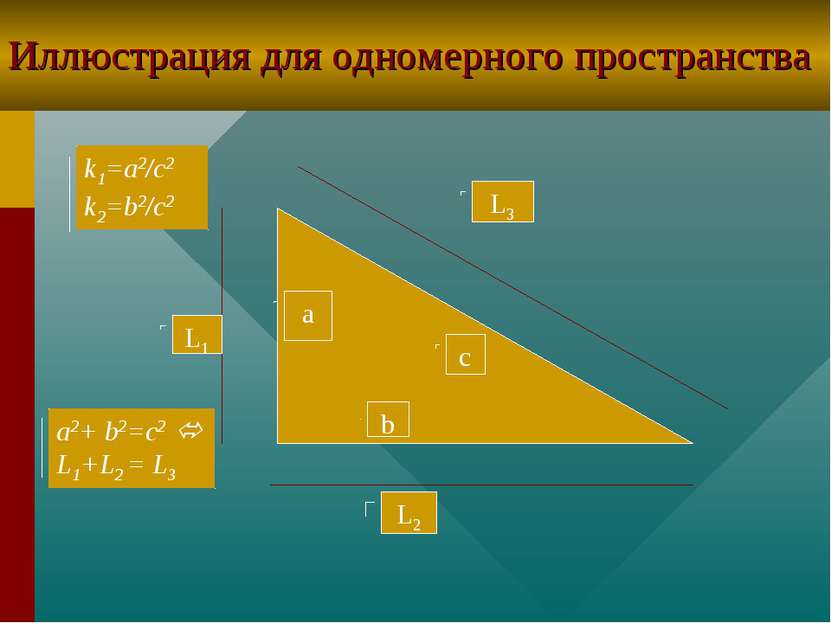
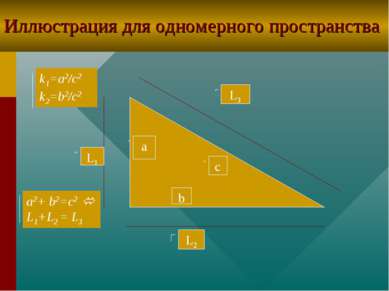
 Теоремы 5 и 6 для одномерного пространства Т5. Если F1 подобна F3, где к=а2/с2, F2 подобна F3 , где к=b2/c2, и L1+L2=L3 , то a,b и с - стороны прямоугольного треугольника . Т6. Если F1 подобна F3, где к=а2/с2, F2 подобна F3 , где к=b2/c2, и а,b и с - стороны прямоугольного треугольника , то L1+L2=L3 .
Теоремы 5 и 6 для одномерного пространства Т5. Если F1 подобна F3, где к=а2/с2, F2 подобна F3 , где к=b2/c2, и L1+L2=L3 , то a,b и с - стороны прямоугольного треугольника . Т6. Если F1 подобна F3, где к=а2/с2, F2 подобна F3 , где к=b2/c2, и а,b и с - стороны прямоугольного треугольника , то L1+L2=L3 .