X
Код презентации скопируйте его
Математика и архитектура
Скачать эту презентацию
Презентация на тему Математика и архитектура
Скачать эту презентациюCлайд 1
Математика и архитектура
Cлайд 2
Ни один из видов искусств так тесно не связан с геометрией, как архитектура. «Окружающий нас мир – это мир геометрии чистой, истинной, безупречной в наших глазах. Все вокруг – геометрия. никогда мы не видим так ясно таких форм, как круг, прямоугольник, угол, угол, цилиндр, шар, выполненных с такой тщательностью и так уверенно».
Cлайд 3
«Возвышенное чудо мира!» Так восторженно писал об архитектурном облике собора Св. Петра в Риме Вильгельм Генрих Ваккенродер. В самом деле, строительство каменного купола собора диаметром 42 м представляло собой сложнейшую техническую задачу. достаточно сказать, что за всю историю человечества построено только 4 сооружения, имеющих каменный купол диаметром более 40 м!
Cлайд 4
История строительства и дальнейшего существования собора полна драматических событий. Так, в 1740 ., через 150 лет после сооружения купола, некоторые трещины, неизбежно возникающие в кладке, расширились до угрожающих размеров. Это событие стимулировало новые теоретические исследования. История собора Св. Петра в Риме убеждает в том, что зодчество представляет собой сложный узел научных, технических и эстетических проблем.
Cлайд 5
Прочность пирамид недосягаема. Желая прославить своего фараона в веках, древнеегипетские зодчие из всех геометрических тел выбрали именно пирамиду. Выбор этот не случаен, ибо в условиях земного тяготения пирамида является наиболее устойчивой конструкцией, способной существовать в веках без риска обвалиться или рассыпаться. Главное правило устойчивости конструкции – уменьшение ее массы по мере увеличения высоты над землей – выражено в пирамиде с предельной ясностью и симметрией.
Cлайд 6
Конструкция древнеегипетской пирамиды является самой простой, прочной и устойчивой. Вес каждого верхнего блока пирамиды по всей поверхности передается нижним блокам. Форма пирамиды представляет полное единство с ее конструкций. Однако такая конструкция не создает внутреннего объема и, по существу не является архитектурной конструкцией.
Cлайд 7
Cлайд 8
Простейшей и древнейший архитектурной конструкцией является стоечно – балочная система. ее прототипом был дольмен – культовое сооружение, состоящее из двух вертикально поставленных камней, на которые наши предки водрузили третий горизонтальный камень. Разумеется, стоечно - балочная конструкция проигрывала пирамиде в устойчивости и распределении веса, но она позволяла создавать внутренние объемы. главным недостатком такой конструкции было то, что камень плохо работает на изгиб. Каменный брус сечением 10х10 см и длиной 1м 34см обламывается под собственным весом. Вот почему в храме Амона в Карнаке мы видим такой лес колонн. на рисунке изображен Храм Амона в Карнаке
Cлайд 9
Комплекс Стонхендж. Развитие стоечно-балочной конструкции.
Cлайд 10
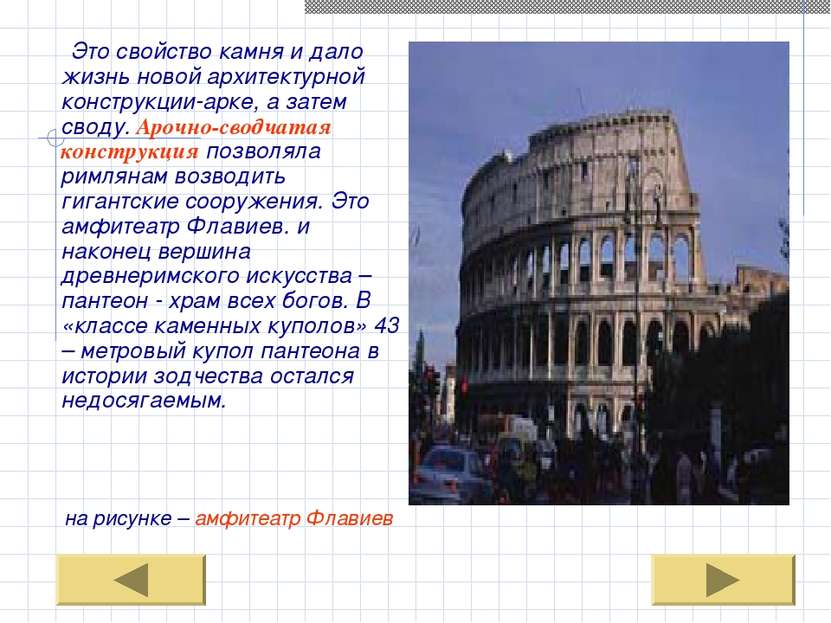
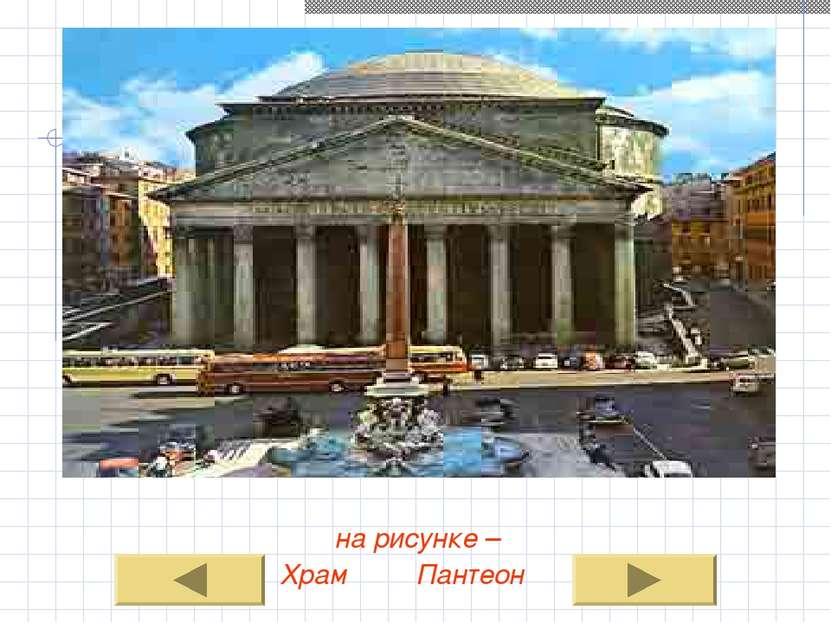
Это свойство камня и дало жизнь новой архитектурной конструкции-арке, а затем своду. Арочно-сводчатая конструкция позволяла римлянам возводить гигантские сооружения. Это амфитеатр Флавиев. и наконец вершина древнеримского искусства – пантеон - храм всех богов. В «классе каменных куполов» 43 – метровый купол пантеона в истории зодчества остался недосягаемым. на рисунке – амфитеатр Флавиев
Cлайд 11
на рисунке – Храм Пантеон
Cлайд 12
Римские термы Каракаллы. Развитие арочно-сводчатой конструкции.
Cлайд 13
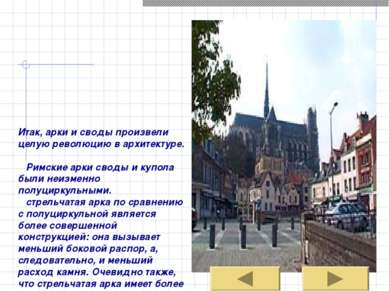Итак, арки и своды произвели целую революцию в архитектуре. Римские арки своды и купола были неизменно полуциркульными. стрельчатая арка по сравнению с полуциркульной является более совершенной конструкцией: она вызывает меньший боковой распор, а, следовательно, и меньший расход камня. Очевидно также, что стрельчатая арка имеет более сложную форму по сравнению с полуциркульной. Таким образом, на примере трех конструкций – стоечно - балочной, арочной и стрельчатой – мы видим, что по мере совершенствования конструкции усложняется и ее геометрия. стрельчатая форма арок подчеркивала это безудержное стремление ввысь. самые высокие своды имели соборы северной Франции: собор в Амьене (48м).
Cлайд 14
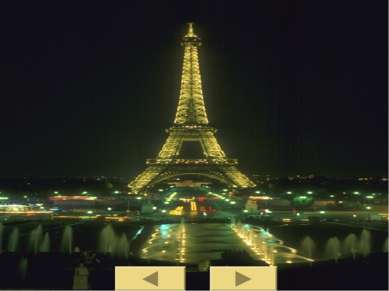
В 1889 г. к открытию Всемирной выставке в Париже как символ победоносного шествия металла в технике была построена знаменитая Эйфелева башня по проекту французского инженера Гюстава Эйфеля. Она сразу вдвое перекрыла все рекорды по преодолению высоты, взметнувшись вверх на 312,6 метра! и, конечно же, бессмертие принесла Эйфелевой башне не ее конструкция, которая сегодня кажется архаичной, а пропорциональность и гармоническое единство ее форм, т.е. как раз то, что и делает строительную конструкцию произведением.
Cлайд 15
Cлайд 16
Cлайд 17
Пропорция – Математика архитектурной гармонии. В чем Красота и Очарование Церкви Покрова на Нерли? Ведь она имеет скромные размеры, ее архитектурные формы крайне не просты, а белокаменные украшения сдержаны и лаконичны. и, тем не менее церковь по праву считается жемчужиной Русской архитектуры. Огромную роль пропорций прекрасно осознавали древнегреческие и древнеегипетские зодчие. В чем же заключается сила архитектурных пропорций? В том что архитектурные пропорции – это Математика Зодчего. а Математика – это Универсальный Язык науки, поэтому мы можем сказать, что пропорции – это Универсальный Язык архитектуры, Язык Всеобъемлющий, Всесильный, как всеобъемлюща и всесильна Математика.
Cлайд 18
Уже Платон глубоко понимал не только математическую, но и эстетическую сущность пропорции. пропорции являются важным и надежным средством зодчего для достижения хрупкого и тонкого– гармония. Пропорциональность является наиболее Ярким, Зримым, Объективным и Математически Закономерным выражением архитектурной гармонии. Пропорция – это Математическая Закономерность, прошедшая через душу Зодчего, это поэзия числа и геометрии в его архитектурном Языке. Вот почему на Языке пропорций говорили Зодчие Всех Времен и Всех архитектурных направлений. К сожалению, ни древние египтяне, ни древние греки не сохранили для потомков секреты своих пропорций. Пифагор знал, по крайней мере, три вида, а Евклид в «Началах» дал развитое математическое учение о пропорциональности и применял правило Золотого сечения для построения правильного пятиугольника!
Cлайд 19
Существует множество доказательств мудрости древних. Так, например, в Неаполе хранится пропорциональный циркуль, найденный при раскопках в Помпеях. Пропорциональный циркуль является необходимым атрибутом архитектора. Он состоит из двух равных по длине ножек, скрепленных винтом наподобие ножниц, и позволяет для любого отрезка получать отрезок, находящийся с ним в заданном отношении. Действие пропорционального циркуля основано на подобии треугольников.
Cлайд 20
Вывод Архитектура – удивительная область человеческой деятельности. В ней тесно связаны и строго уравновешены наука, техника и искусство. Роль математики в формировании ее прочности и пользы очевидна. Архитектура триедина: она извечно сочетает в себе логику ученого, ремесло мастера и вдохновение художника.
