X
Код презентации скопируйте его
Задачи планиметрии. Треугольник
Скачать эту презентацию
Презентация на тему Задачи планиметрии. Треугольник
Скачать эту презентациюCлайд 1
Cлайд 2
Простейший из многоугольников – треугольник – играет в геометрии особую роль. Без преувеличения можно сказать, что вся (или почти вся) геометрия со времён «Начал» Евклида покоится на «трёх китах» - трёх признаках равенства треугольников.
Cлайд 3
Исторический материал Любой геометрический материал возникает из потребностей окружающей жизни. Доказательство признаков равенства треугольников приписывают древнегреческому ученому Фалесу Милетскому (жившему ок.625-547г.г. до н.э.). Теорему о равенстве треугольников по стороне и прилежащим к ней двум углам он использовал для определения расстояния от берега до морских кораблей.
Cлайд 4
В древнем искусстве очень широко распространяются изображения равностороннего треугольника . Первобытные люди штамповали треугольники на разных изделиях. Вожди племен северо-американских индейцев носили на груди символ власти: равносторонний треугольник с точкой в центре, в Африке женщины также украшают себя большими пластинами из равносторонних треугольников. Равносторонние треугольники рисовали на изображениях священных животных.
Cлайд 5
Для составления красивых паркетов часто использовали треугольники .
Cлайд 6
Лишь на рубеже XIX – XX веков математики научились строить геометрию на основе более фундаментального и общего, чем равенство треугольников, понятия геометрического преобразования. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о «геометрии треугольника» как о самостоятельном разделе элементарной геометрии.
Cлайд 7
Вопрос 1. Определение треугольника С В А
Cлайд 8
Вопрос 2. Определение остроугольного треугольника А С В
Cлайд 9
С А В Вопрос 3. Определение прямоугольного треугольника
Cлайд 10
О Т Вопрос 4. Определение тупоугольного треугольника Н
Cлайд 11
Вопрос 5. Определение равностороннего треугольника А С В
Cлайд 12
Вопрос 6. Определение равнобедренного треугольника М С О
Cлайд 13
Вопрос 7. Медиана треугольника (определение) А В С М
Cлайд 14
Вопрос 8. Медианы треугольника (замечательное свойство) А В С М Р К
Cлайд 15
Вопрос 9. Свойство медианы равнобедренного треугольника А В С М
Cлайд 16
Вопрос 10. Биссектриса треугольника (определение) О А В С
Cлайд 17
Вопрос 11. Биссектрисы треугольника ( свойство) К А В С Н М
Cлайд 18
Вопрос 12. Биссектриса равнобедренного треугольника К А В С
Cлайд 19
Вопрос 13. Высота треугольника А С В Н АН ВС
Cлайд 20
Вопрос 14. Высоты треугольника (замечательное свойство)
Cлайд 21
Вопрос 15. Свойство высоты равнобедренного треугольника А С В Н
Cлайд 22
Вопрос 16. Свойство углов при основании равнобедренного треугольника К В С
Cлайд 23
Вопрос 17. Равные треугольники
Cлайд 24
Вопрос 18. Первый признак равенства треугольников (По двум сторонам и углу между ними )
Cлайд 25
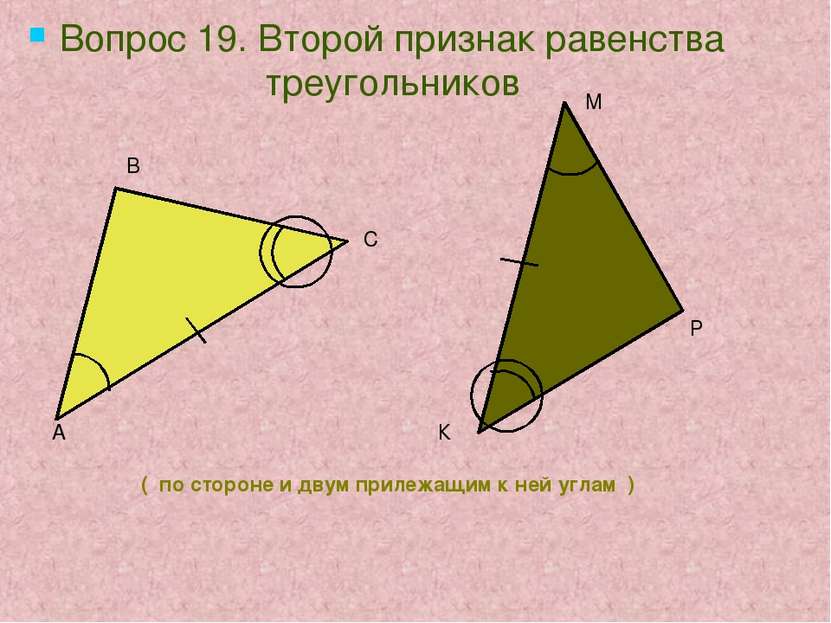
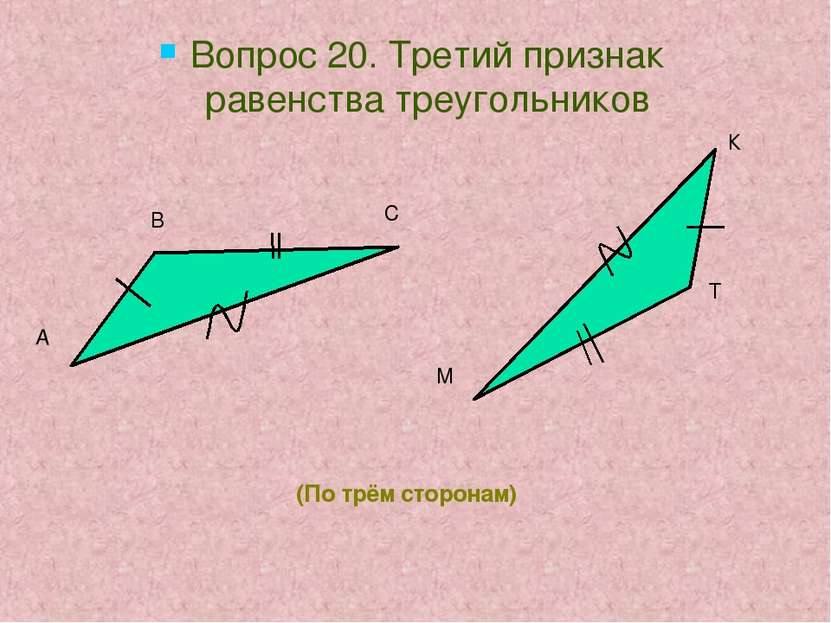
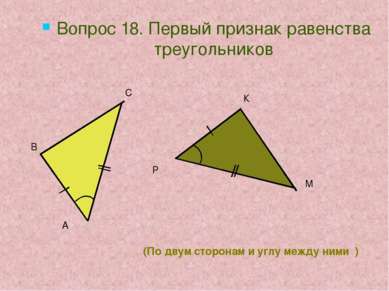
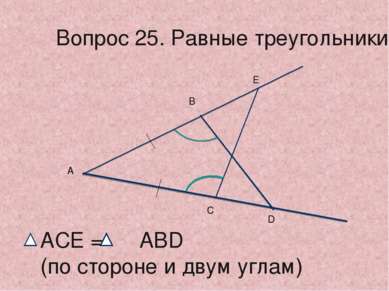
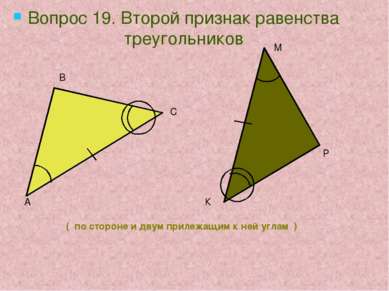( по стороне и двум прилежащим к ней углам ) Вопрос 19. Второй признак равенства треугольников
Cлайд 26
(По трём сторонам) Вопрос 20. Третий признак равенства треугольников
Cлайд 27
Вопрос 21. Равные треугольники AOB= COD (по стороне и двум углам)
Cлайд 28
D E C K S Вопрос 22. Равные треугольники DEC= DKC (по двум сторонам и углу)
Cлайд 29
1 2 А С D В Вопрос 23. Равные треугольники ADB= ADC (по двум сторонам и углу)
Cлайд 30
D E C K Вопрос 24. Равные треугольники DEC = DKC (по трем сторонам)
Cлайд 31
А В Е С D АСЕ = АВD (по стороне и двум углам) Вопрос 25. Равные треугольники
Cлайд 32
С А В F Вопрос 26. Равные треугольники CAF = CBF (по трем сторонам)
Cлайд 33
О А В С D Е Вопрос 27. Равные треугольники CAE= DBE (по двум сторонам и углу)
Cлайд 34
СОСЧИТАЙ ТРЕУГОЛЬНИКИ Вопрос 28.
Cлайд 35
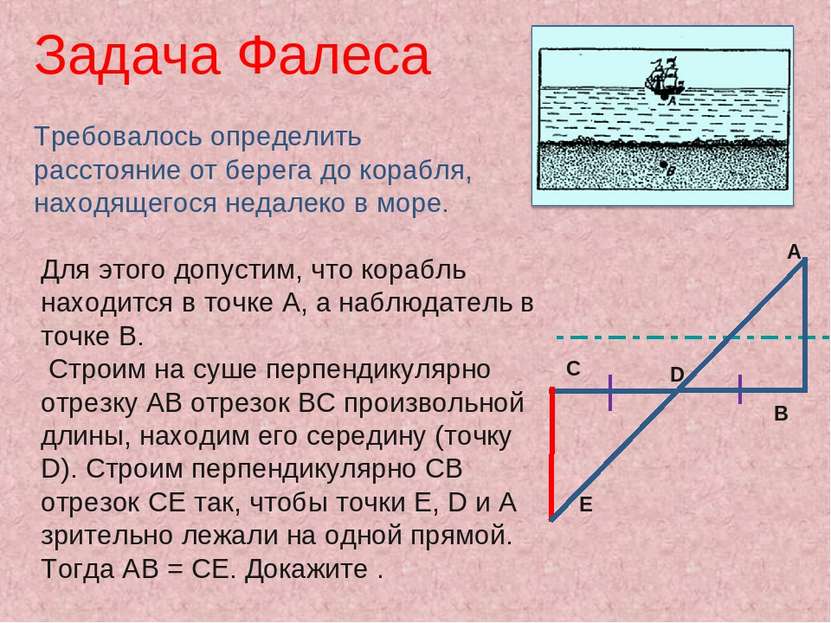
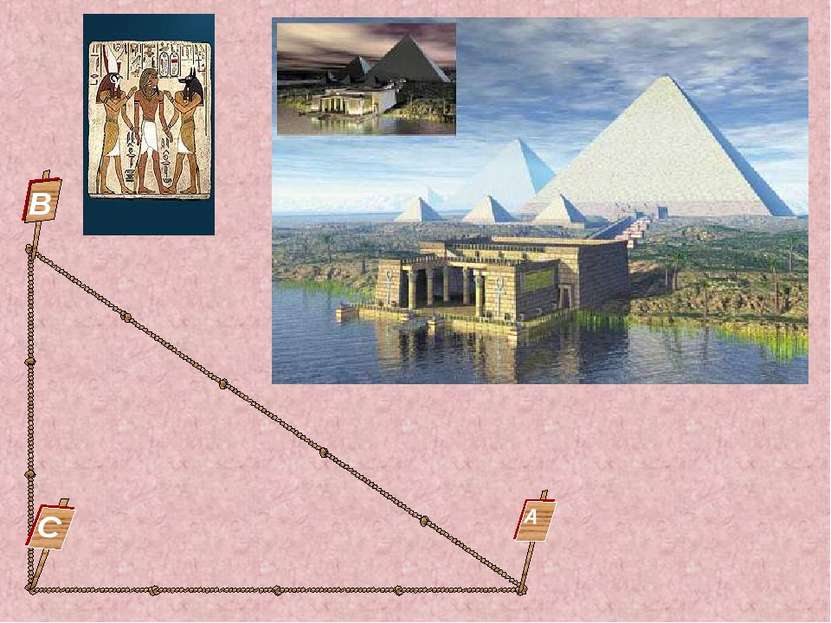
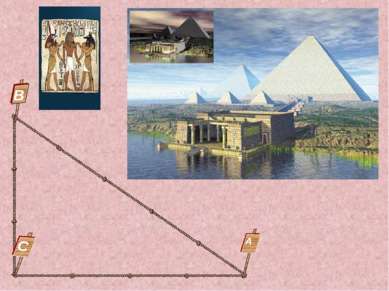
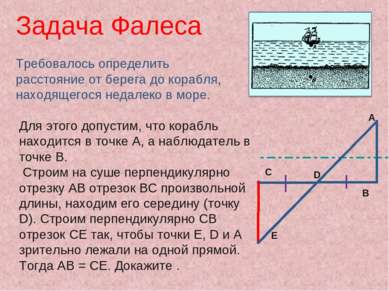Для этого допустим, что корабль находится в точке A, а наблюдатель в точке B. Строим на суше перпендикулярно отрезку AB отрезок BC произвольной длины, находим его середину (точку D). Строим перпендикулярно CB отрезок CE так, чтобы точки E, D и A зрительно лежали на одной прямой. Тогда AB = CE. Докажите . Задача Фалеса Требовалось определить расстояние от берега до корабля, находящегося недалеко в море. Е С D А B
Cлайд 36
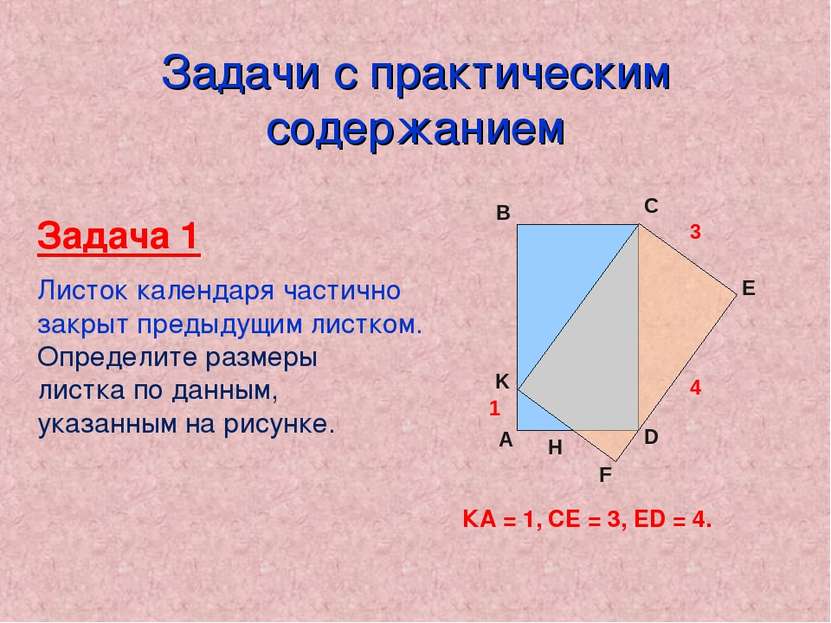
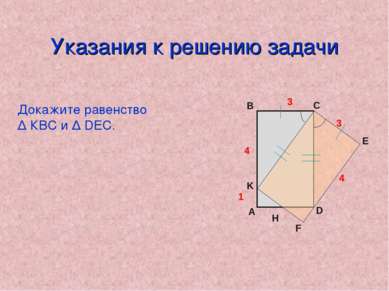
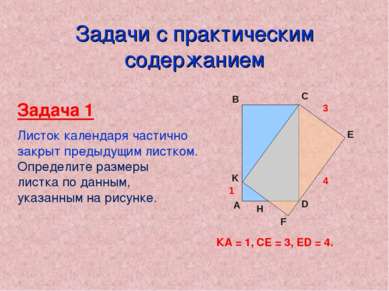Задачи с практическим содержанием Задача 1 Листок календаря частично закрыт предыдущим листком. Определите размеры листка по данным, указанным на рисунке. Н 1 3 4 КА = 1, СЕ = 3, ED = 4.
Cлайд 37
Указания к решению задачи 1 4 3 Н 4 3 Докажите равенство ∆ КВС и ∆ DEС.
Cлайд 38
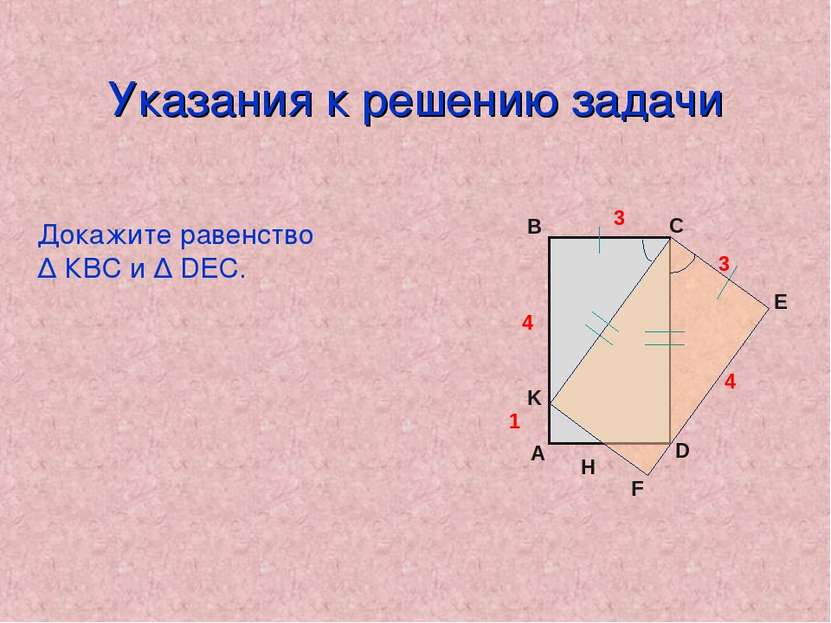
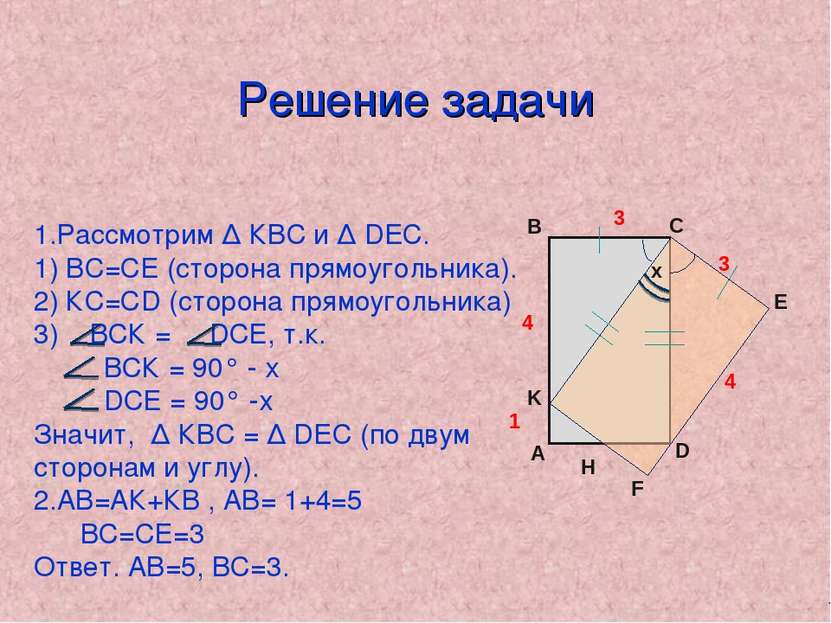
Решение задачи 1 4 3 Н 4 3 Рассмотрим ∆ КВС и ∆ DEС. 1) ВС=СЕ (сторона прямоугольника). 2) КС=СD (сторона прямоугольника) ВСК = DСЕ, т.к. ВСК = 90° - х DСЕ = 90° -х Значит, ∆ КВС = ∆ DEС (по двум сторонам и углу). АВ=АК+КВ , АВ= 1+4=5 ВС=СЕ=3 Ответ. АВ=5, ВС=3. х
Cлайд 39
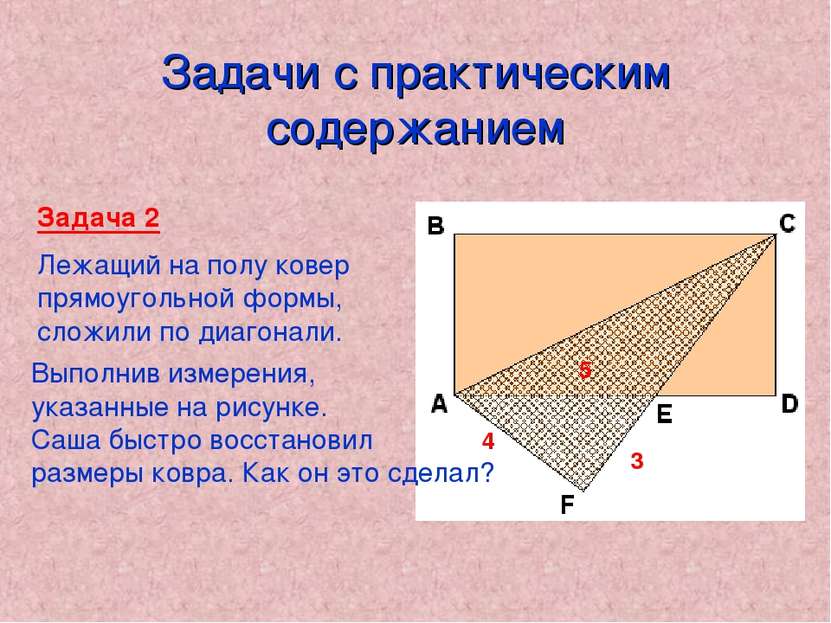
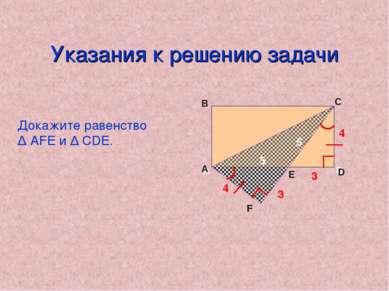
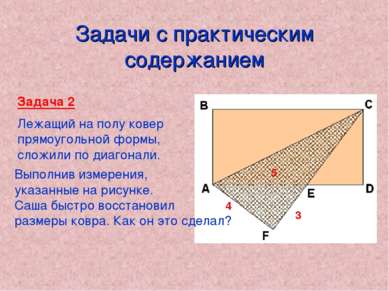Задачи с практическим содержанием Задача 2 Лежащий на полу ковер прямоугольной формы, сложили по диагонали. Выполнив измерения, указанные на рисунке. Саша быстро восстановил размеры ковра. Как он это сделал? 4 3 5
Cлайд 40
Указания к решению задачи Докажите равенство ∆ AFE и ∆ CDE. 4 3 3 4 5 5
Cлайд 41
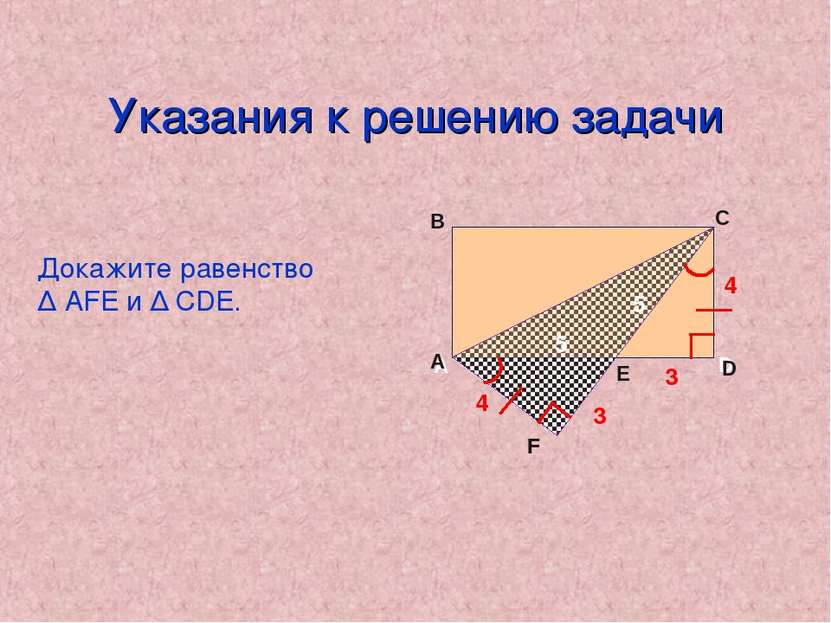
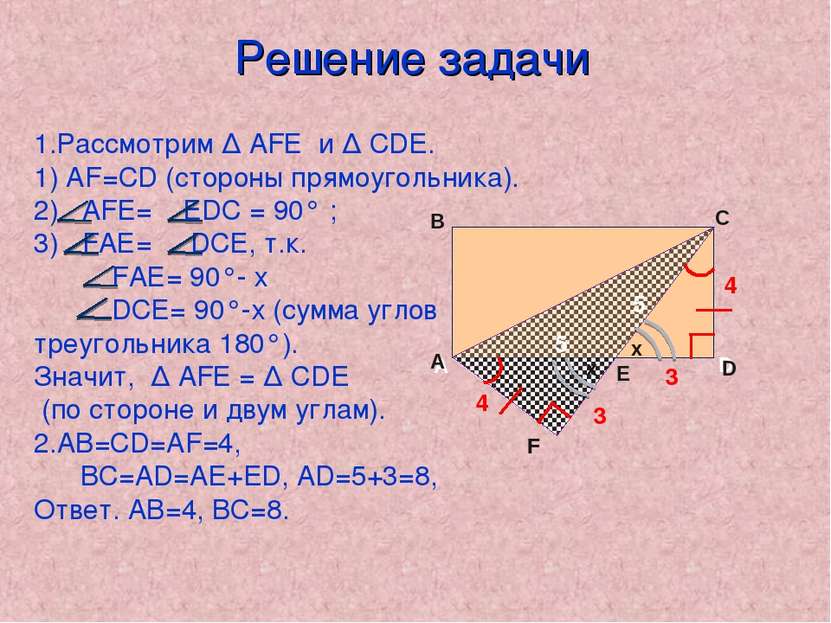
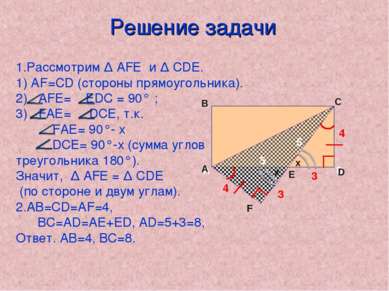Pешениe задачи 4 3 3 4 5 5 Рассмотрим ∆ АFЕ и ∆ СDE. 1) АF=СD (стороны прямоугольника). АFЕ= ЕDС = 90° ; FАЕ= DСЕ, т.к. FАЕ= 90°- х DСЕ= 90°-х (сумма углов треугольника 180°). Значит, ∆ АFЕ = ∆ СDE (по стороне и двум углам). АВ=CD=АF=4, ВС=AD=AЕ+ED, AD=5+3=8, Ответ. АВ=4, ВС=8. х х
Cлайд 42
С В
Cлайд 43
19 марта 2010 года Шуховской башне на Шаболовке исполнилось 88 лет.
Cлайд 44
Высоковольтные линии электропередачи. Треугольники делают конструкции надежными.
Cлайд 45
Треугольники в конструкции мостов.
Cлайд 46
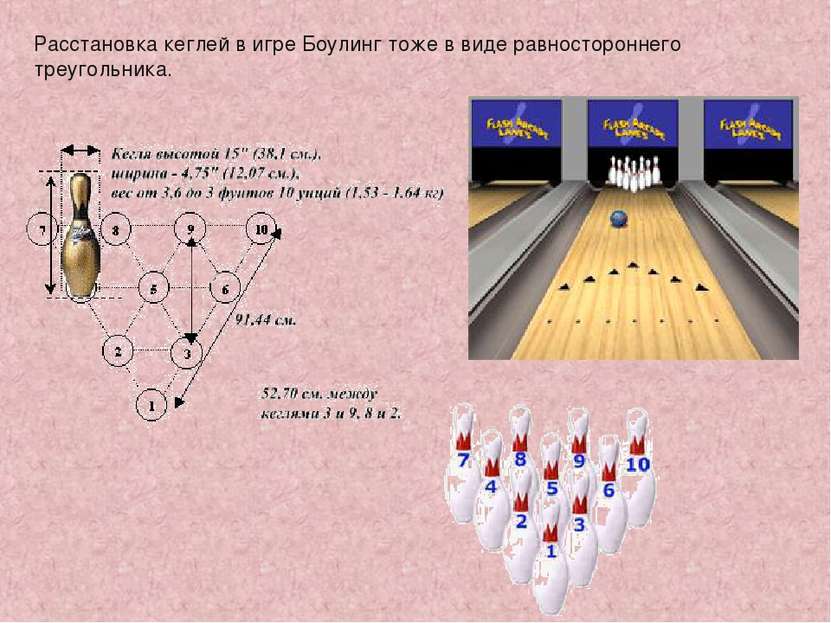
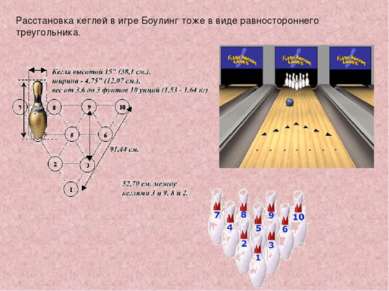
Начиная игру в бильярд, необходимо расположить шары в виде треугольника. Для этого используют специальную треугольную рамку.
Cлайд 47
Расстановка кеглей в игре Боулинг тоже в виде равностороннего треугольника.
Cлайд 48
Треуго льник — ударный музыкальный инструмент в виде металлического прута , изогнутого в форме треугольника. Один из углов оставлен открытым (концы прута почти касаются).
Cлайд 49
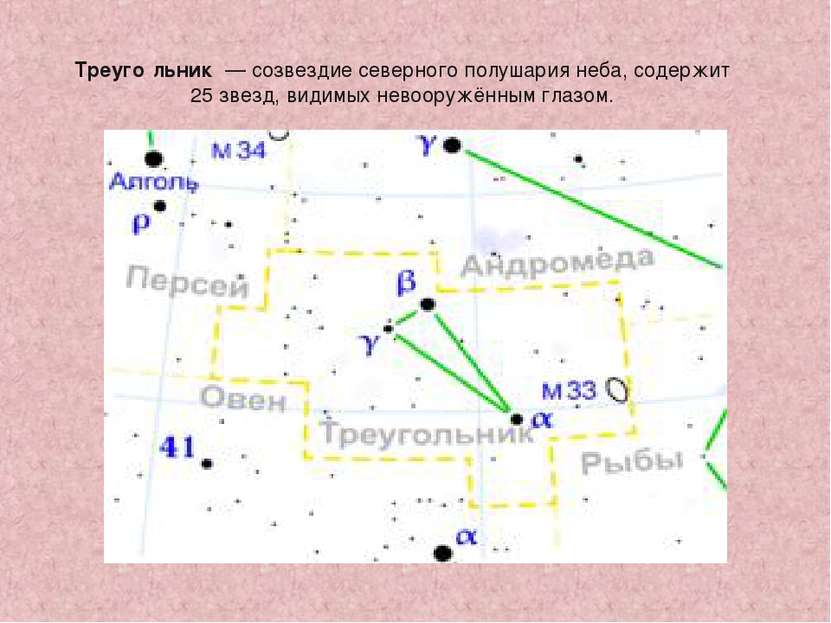
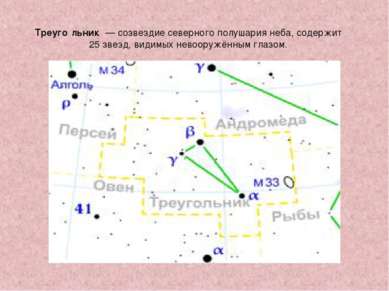Треуго льник — созвездие северного полушария неба, содержит 25 звезд, видимых невооружённым глазом.
Cлайд 50
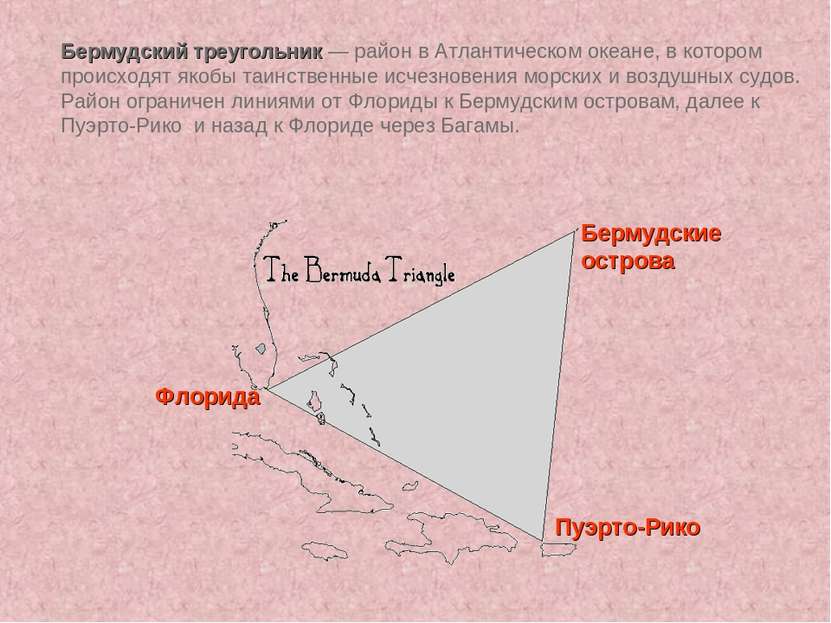
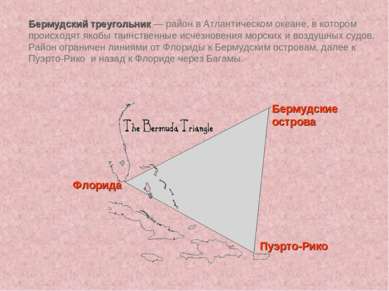Бермудский треугольник — район в Атлантическом океане, в котором происходят якобы таинственные исчезновения морских и воздушных судов. Район ограничен линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и назад к Флориде через Багамы. Пуэрто-Рико Флорида Бермудские острова
Cлайд 51
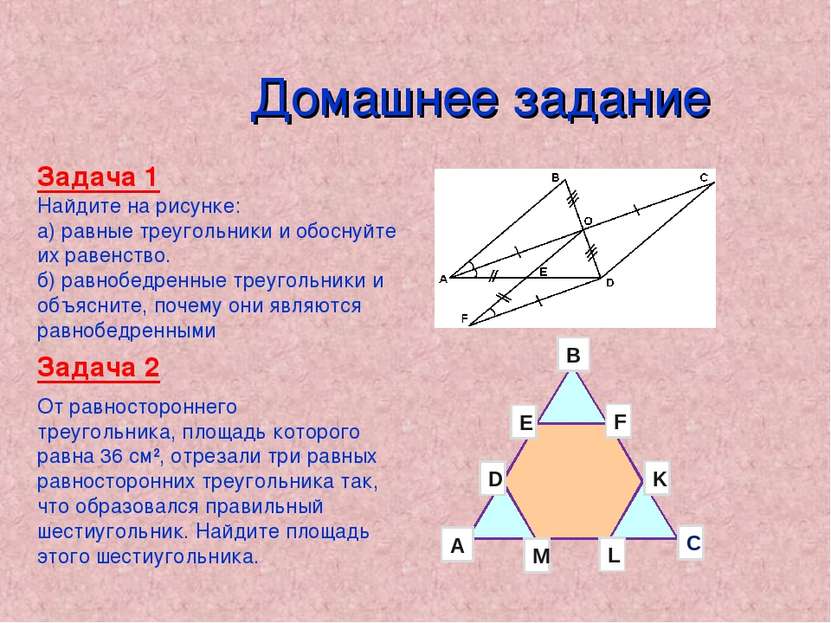
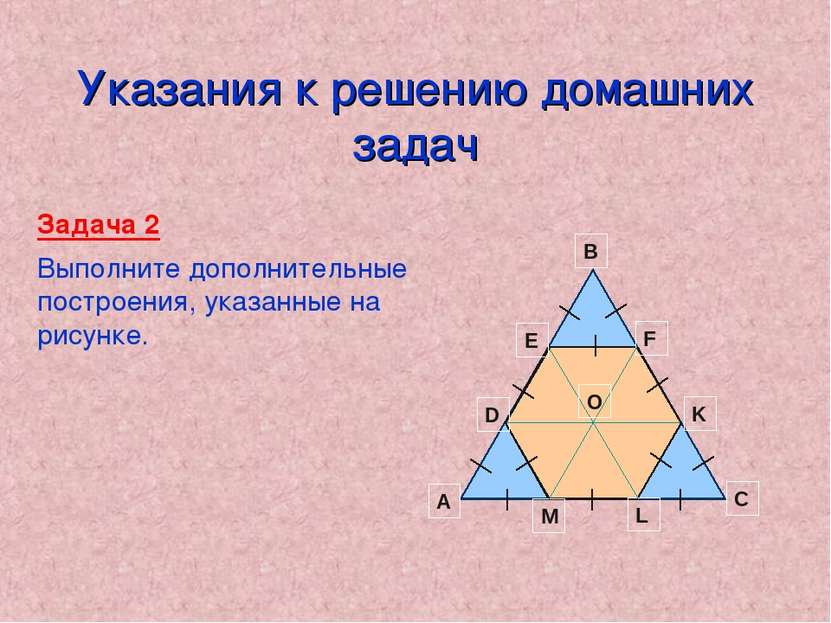
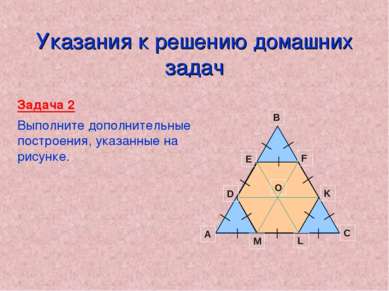
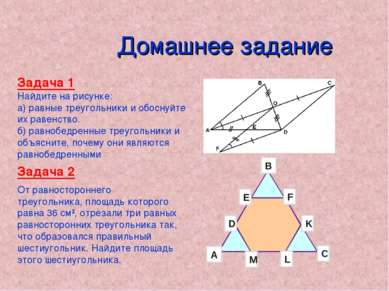Домашнее задание Задача 1 Найдите на рисунке: а) равные треугольники и обоснуйте их равенство. б) равнобедренные треугольники и объясните, почему они являются равнобедренными Задача 2 От равностороннего треугольника, площадь которого равна 36 см2, отрезали три равных равносторонних треугольника так, что образовался правильный шестиугольник. Найдите площадь этого шестиугольника.
Cлайд 52
Указания к решению домашних задач Задача 2 Выполните дополнительные построения, указанные на рисунке.
Cлайд 53
Спасибо за урок !
