X
Код презентации скопируйте его
Магический квадрат
Скачать эту презентацию
Презентация на тему Магический квадрат
Скачать эту презентациюCлайд 1
Магический или волшебный квадрат — это квадратная таблица, заполненная числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Магические квадраты
Cлайд 2
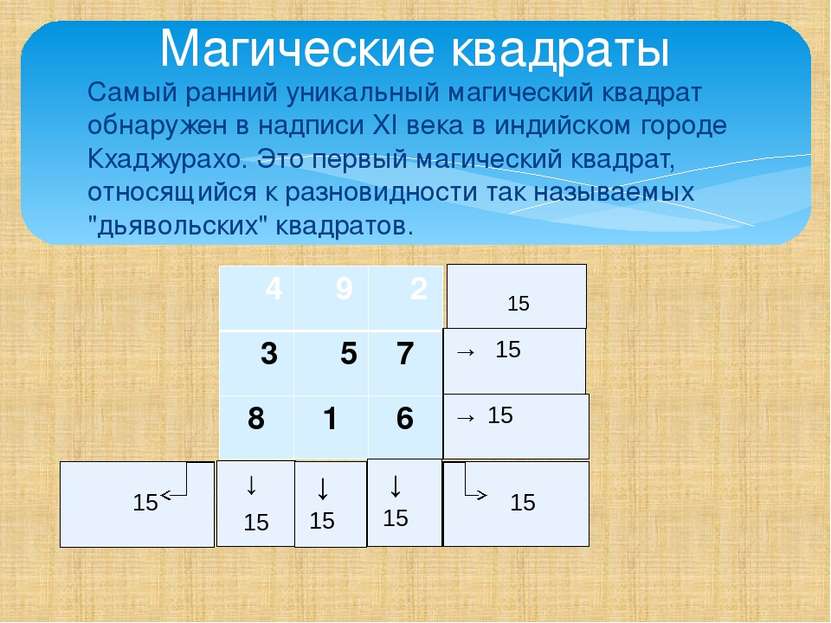
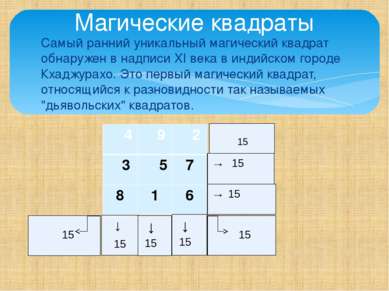Самый ранний уникальный магический квадрат обнаружен в надписи XI века в индийском городе Кхаджурахо. Это первый магический квадрат, относящийся к разновидности так называемых "дьявольских" квадратов. → Магические квадраты 4 9 2 3 5 7 8 1 6 15 →15 →15 ↓ 15 ↓ 15 ↓ 15 15 15
Cлайд 3
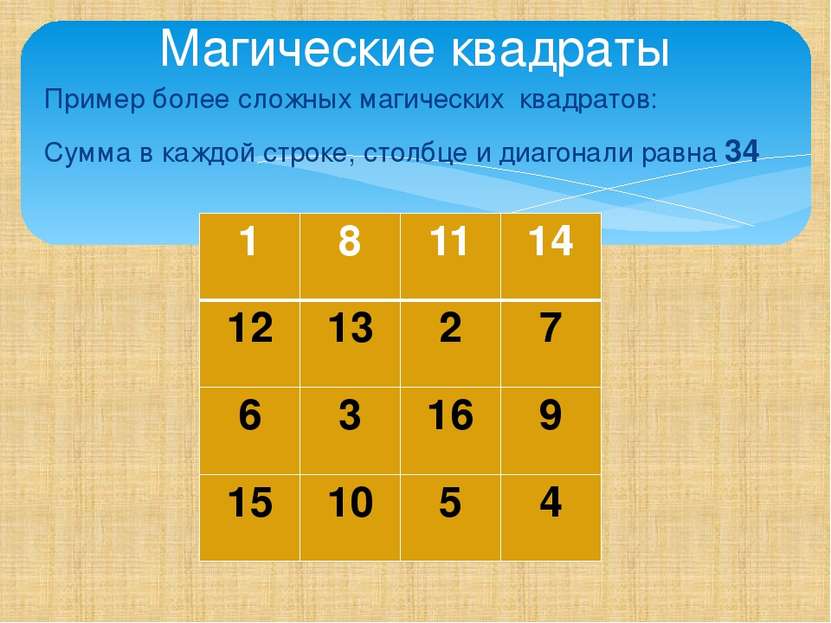
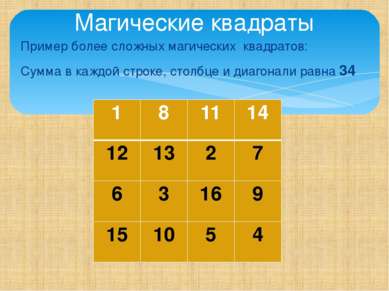Пример более сложных магических квадратов: Сумма в каждой строке, столбце и диагонали равна 34 Магические квадраты 1 8 11 14 12 13 2 7 6 3 16 9 15 10 5 4
Cлайд 4
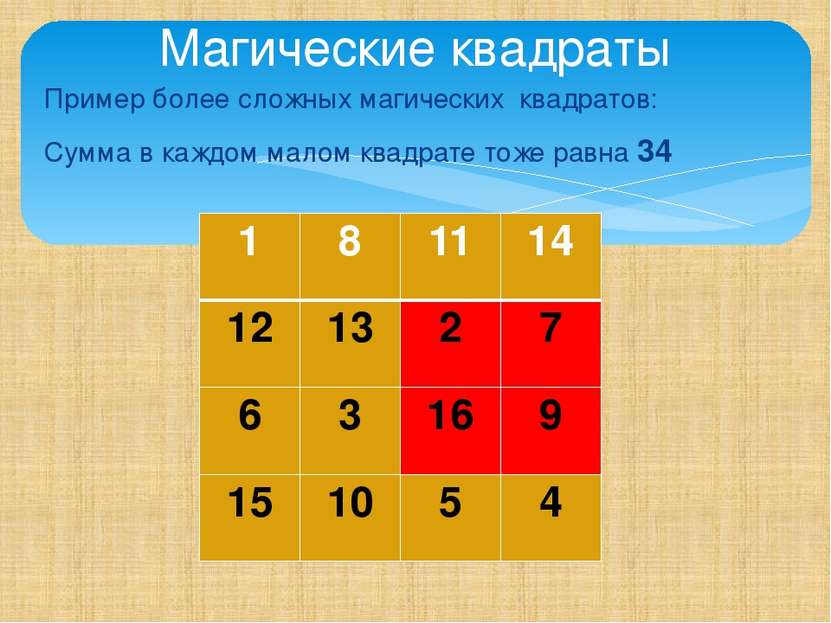
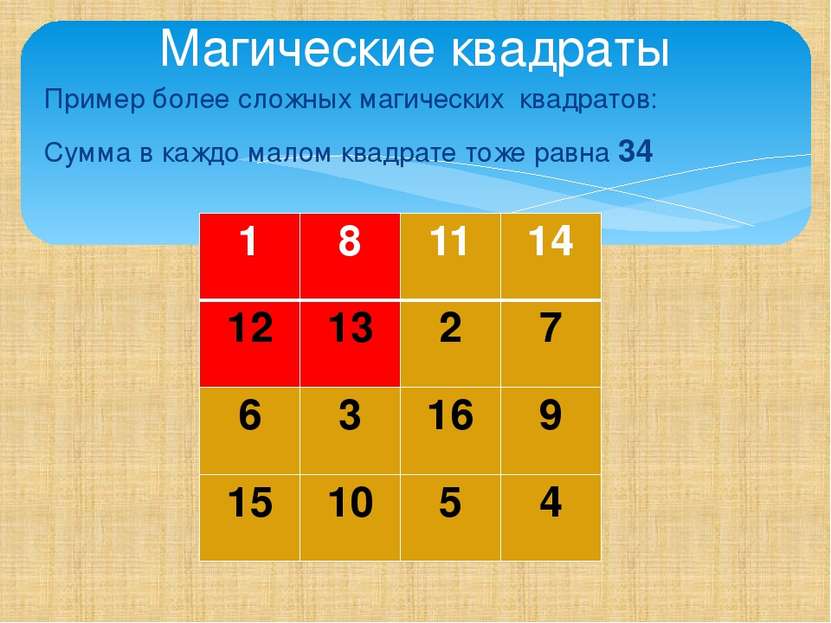
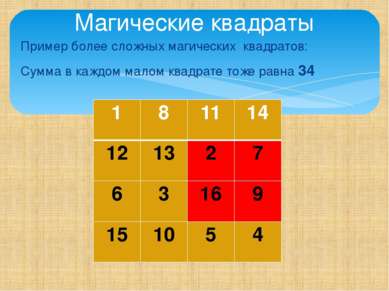Пример более сложных магических квадратов: Сумма в каждом малом квадрате тоже равна 34 Магические квадраты 1 8 11 14 12 13 2 7 6 3 16 9 15 10 5 4
Cлайд 5
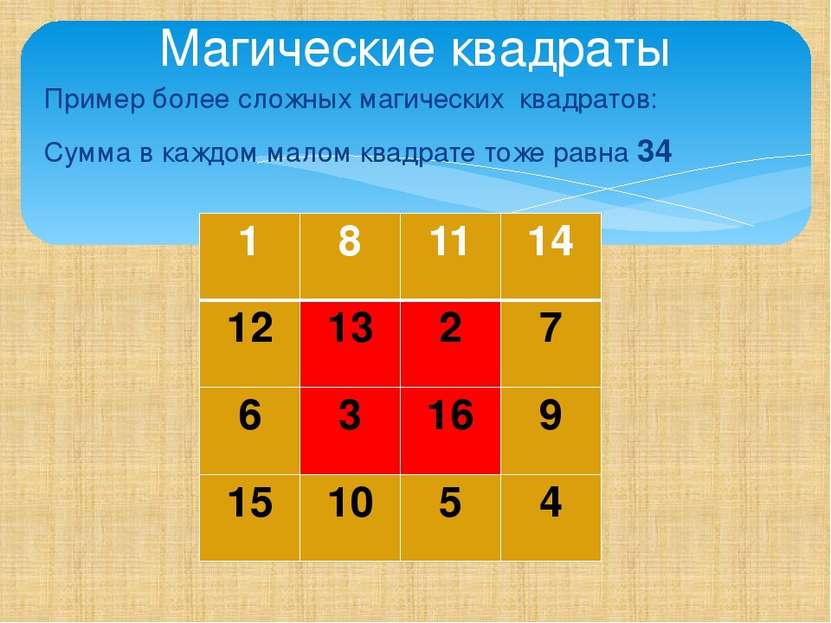
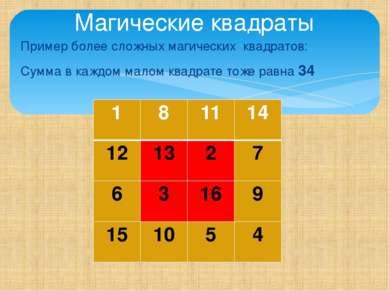Пример более сложных магических квадратов: Сумма в каждом малом квадрате тоже равна 34 Магические квадраты 1 8 11 14 12 13 2 7 6 3 16 9 15 10 5 4
Cлайд 6
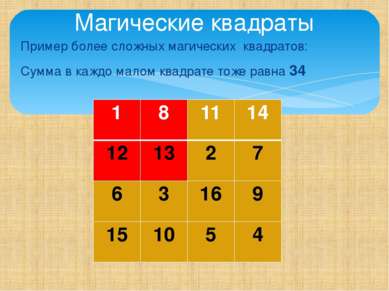Пример более сложных магических квадратов: Сумма в каждо малом квадрате тоже равна 34 Магические квадраты 1 8 11 14 12 13 2 7 6 3 16 9 15 10 5 4
Cлайд 7
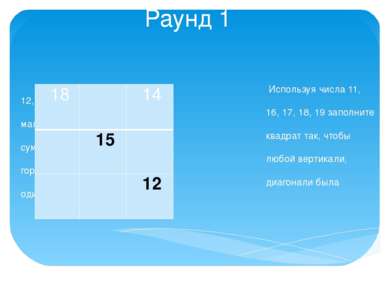Раунд 1 Используя числа 11, 12, 13, 14, 15, 16, 17, 18, 19 заполните магический квадрат так, чтобы сумма чисел по любой вертикали, горизонтали и диагонали была одинаковой. 18 14 15 12
Cлайд 8
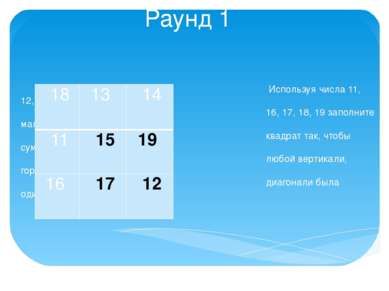Раунд 1 Используя числа 11, 12, 13, 14, 15, 16, 17, 18, 19 заполните магический квадрат так, чтобы сумма чисел по любой вертикали, горизонтали и диагонали была одинаковой. 18 13 14 11 15 19 16 17 12
Cлайд 9
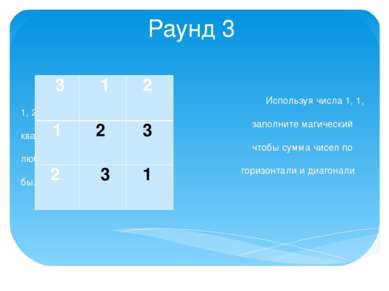
Раунд 2 Используя числа 1, 2, 3, 4, 5, 6, 7, 8, 9 заполните магический квадрат так, чтобы сумма чисел по любой вертикали, горизонтали и диагонали была бы одинаковой. 5 2
Cлайд 10
Раунд 2 Используя числа 1, 2, 3, 4, 5, 6, 7, 8, 9 заполните магический квадрат так, чтобы сумма чисел по любой вертикали, горизонтали и диагонали была равна 15. 5 2
Cлайд 11
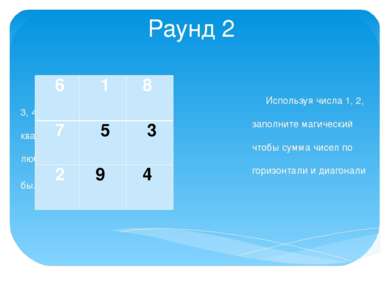Раунд 2 Используя числа 1, 2, 3, 4, 5, 6, 7, 8, 9 заполните магический квадрат так, чтобы сумма чисел по любой вертикали, горизонтали и диагонали была равна 15. 6 1 8 7 5 3 2 9 4
Cлайд 12
Раунд 3 Используя числа 1, 1, 1, 2, 2, 2, 3, 3, 3 заполните магический квадрат так, чтобы сумма чисел по любой вертикали, горизонтали и диагонали была одинаковой
Cлайд 13
Раунд 3 Используя числа 1, 1, 1, 2, 2, 2, 3, 3, 3 заполните магический квадрат так, чтобы сумма чисел по любой вертикали, горизонтали и диагонали была одинаковой 3 1 2 1 2 3 2 3 1
