X
Код презентации скопируйте его
Свойства равнобедренного треугольника
Скачать эту презентацию
Презентация на тему Свойства равнобедренного треугольника
Скачать эту презентациюCлайд 1
Тема: Cвойства равнобедренного треугольника Разработала: Богданова Ольга Николаевна, учитель математики МКОУ «Овечкинская СОШ Завьяловского района» 2014 г Урок геометрии в 7 классе
Cлайд 2
Медианы, биссектрисы и высоты треугольника
Cлайд 3
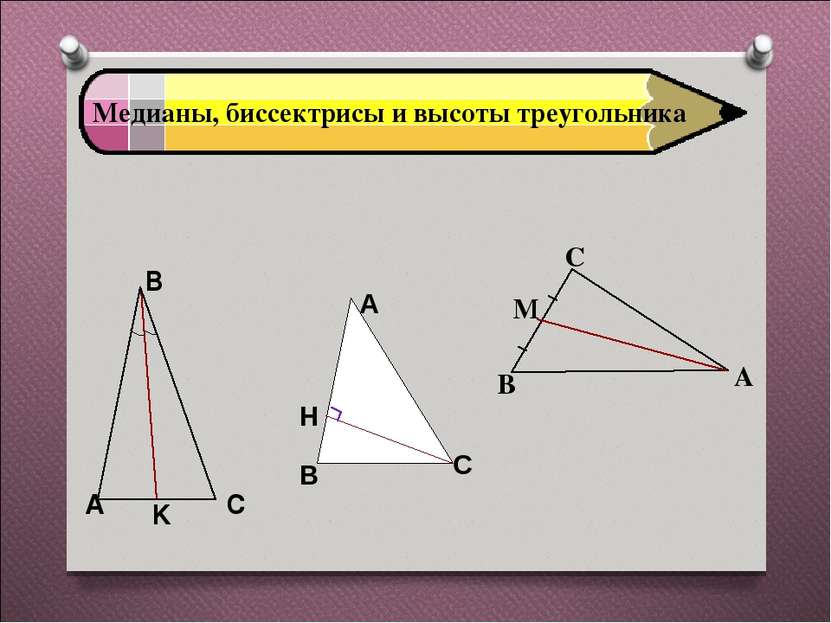
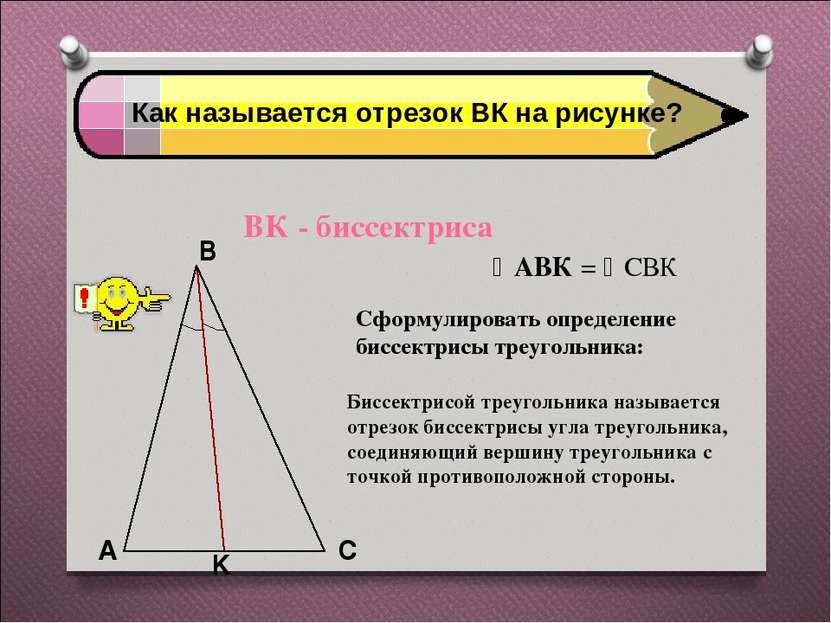
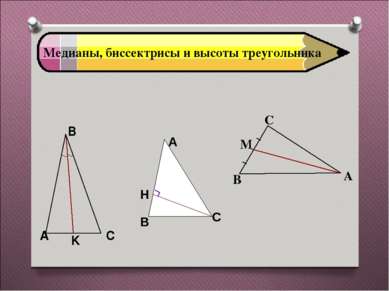
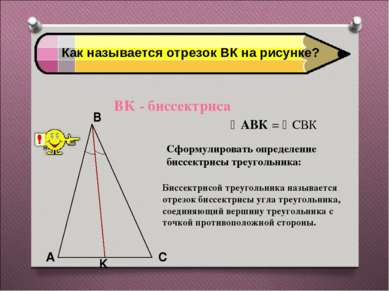Как называется отрезок ВК на рисунке? ВК - биссектриса АВК = СВК Сформулировать определение биссектрисы треугольника: Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Cлайд 4
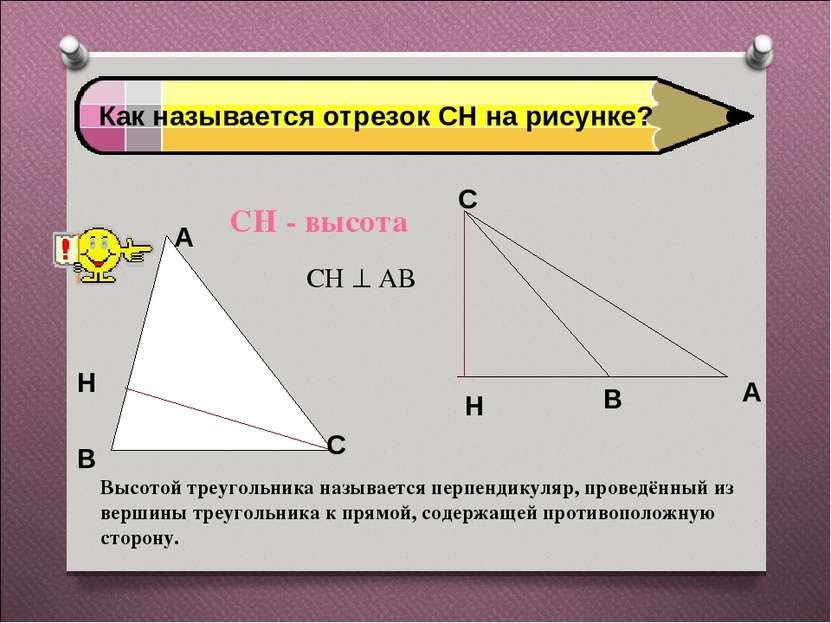
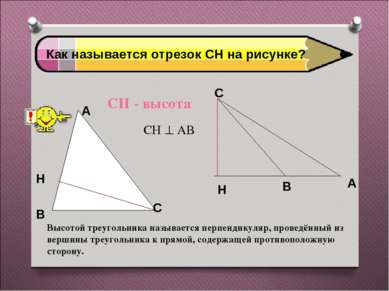Как называется отрезок СН на рисунке? СН - высота СН АВ Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Cлайд 5
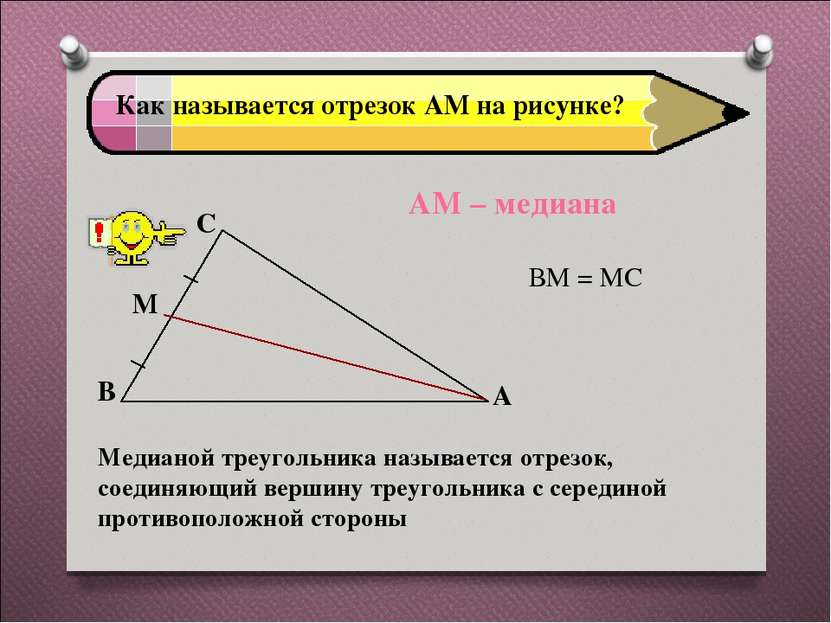
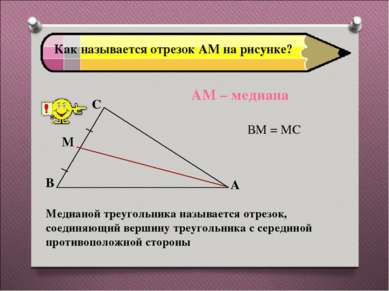Как называется отрезок АМ на рисунке? ВМ = МС АМ – медиана Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны
Cлайд 6
Эти определения надо знать!
Cлайд 7
Словарная работа
Cлайд 8
Разгадайте анаграммы МАПЯРЯ ЧУЛ РЕЗОКОТ ИРЕПТЕМР КРЕТЬЛУТОИН
Cлайд 9
Проверь себя Прямая Луч Отрезок Периметр Треугольник
Cлайд 10
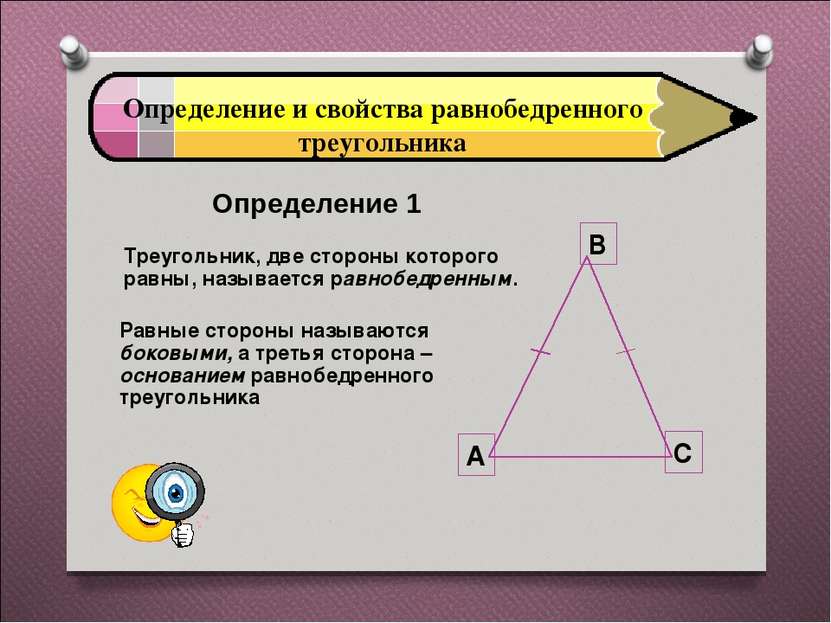
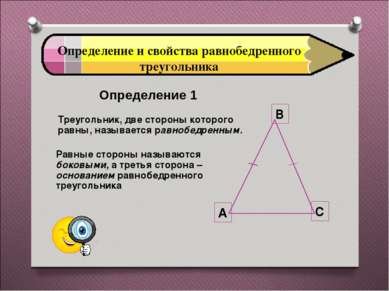Определение и свойства равнобедренного треугольника Определение 1 Треугольник, две стороны которого равны, называется равнобедренным. Равные стороны называются боковыми, а третья сторона – основанием равнобедренного треугольника
Cлайд 11
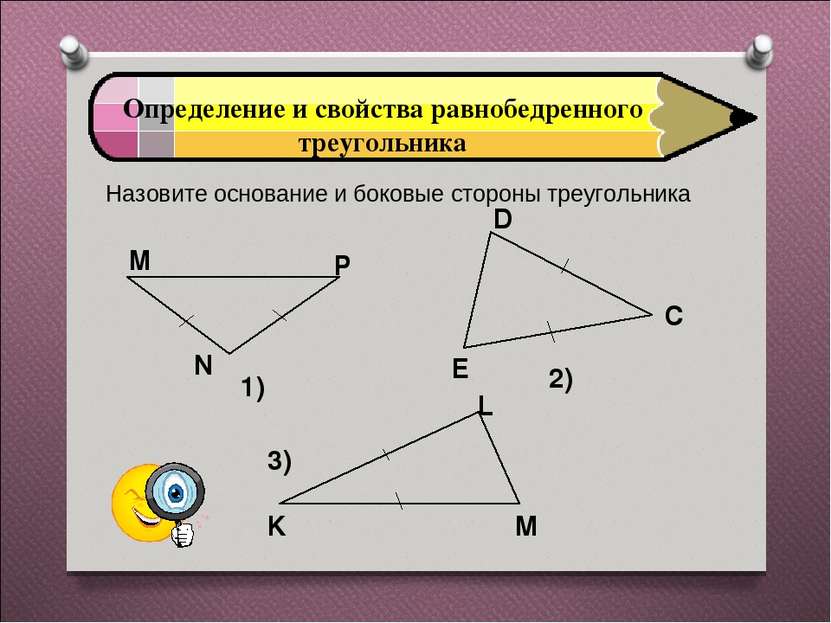
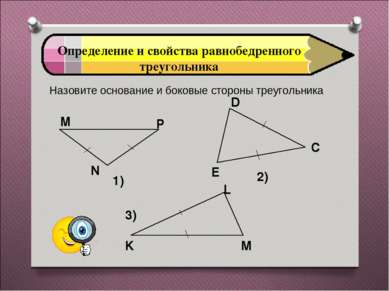Определение и свойства равнобедренного треугольника Назовите основание и боковые стороны треугольника
Cлайд 12
Актуализация знаний Внимательно рассмотри чертежи! 1 2 3 4 5
Cлайд 13
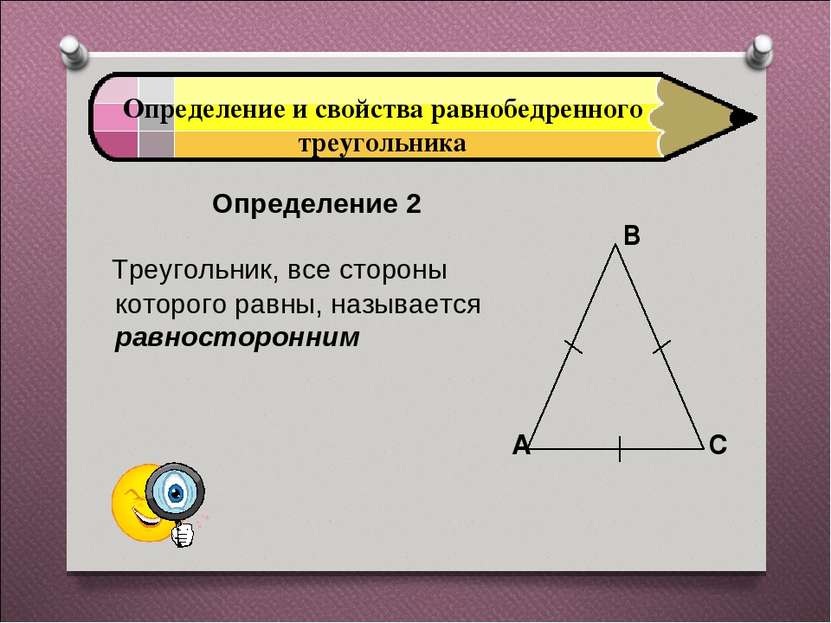
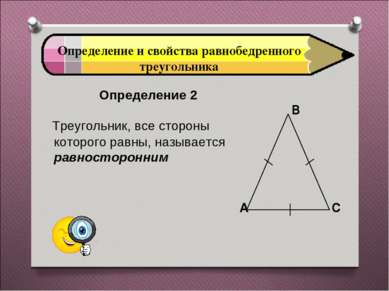Определение и свойства равнобедренного треугольника Определение 2 Треугольник, все стороны которого равны, называется равносторонним
Cлайд 14
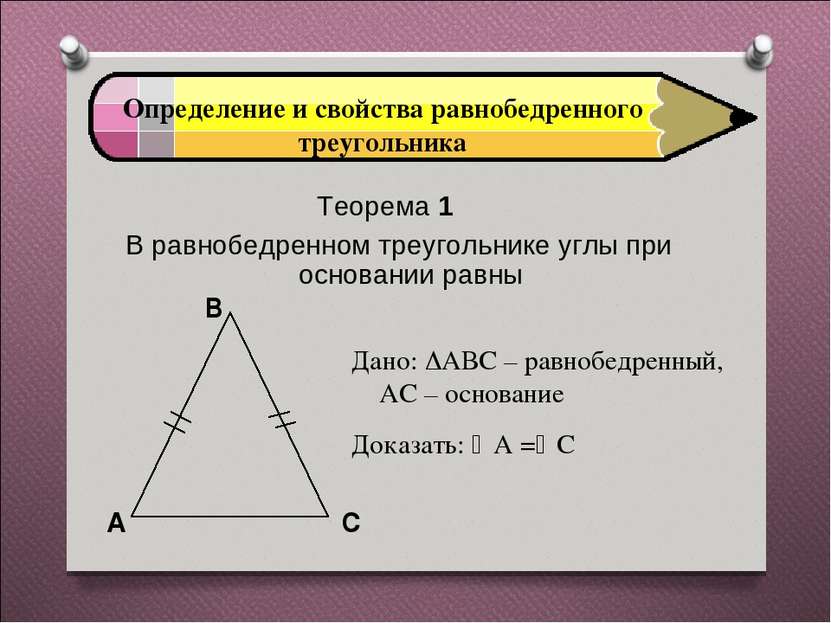
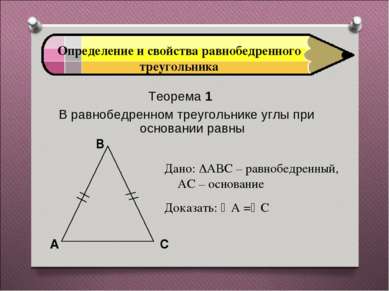Определение и свойства равнобедренного треугольника Теорема 1 В равнобедренном треугольнике углы при основании равны Дано: АВС – равнобедренный, АС – основание Доказать: А = С
Cлайд 15
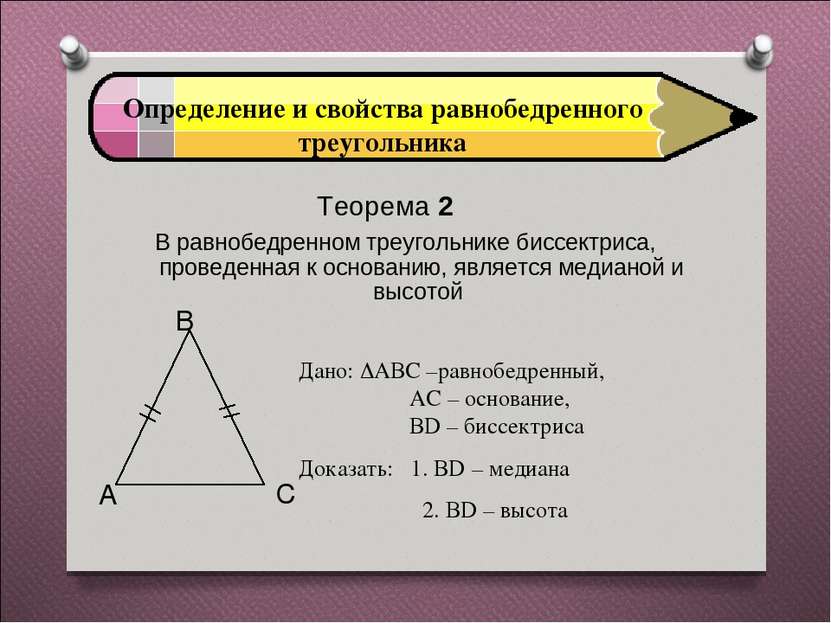
Определение и свойства равнобедренного треугольника Теорема 2 В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой Дано: АВС –равнобедренный, АС – основание, ВD – биссектриса Доказать: 1. ВD – медиана 2. ВD – высота
Cлайд 16
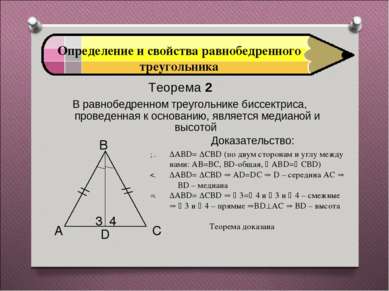Определение и свойства равнобедренного треугольника Теорема 2 В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой АВD= СВD (по двум сторонам и углу между нами: АВ=ВС, ВD-общая, АВD= СВD) АВD= СВD АD=DC D – середина АС ВD – медиана АВD= СВD 3= 4 и 3 и 4 – смежные 3 и 4 – прямые ВD АС ВD – высота Теорема доказана Доказательство:
Cлайд 17
Cлайд 18
Закрепление материала Внимательно рассмотри чертежи! Р О Д А М С К В Х
Cлайд 19
Закрепление материала Сколько всего было треугольников? Ответ: три
Cлайд 20
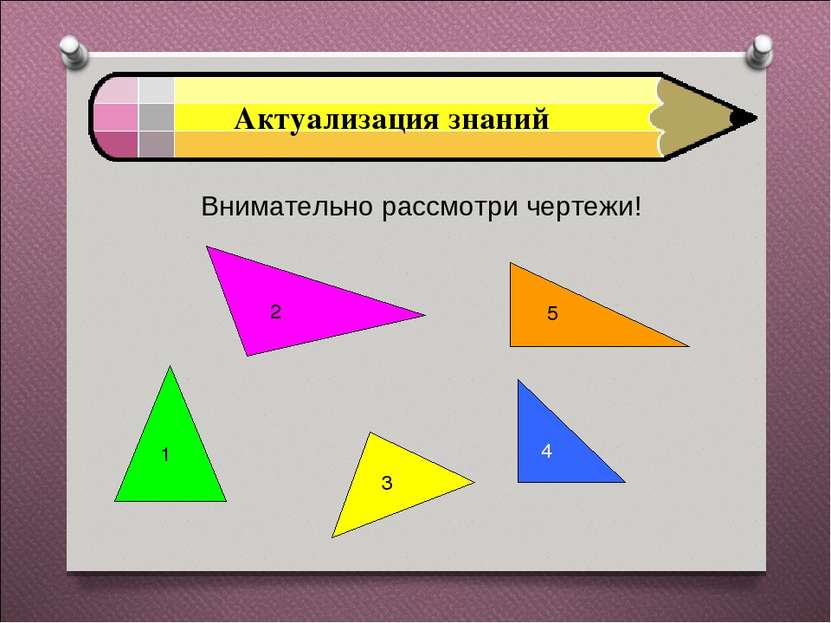
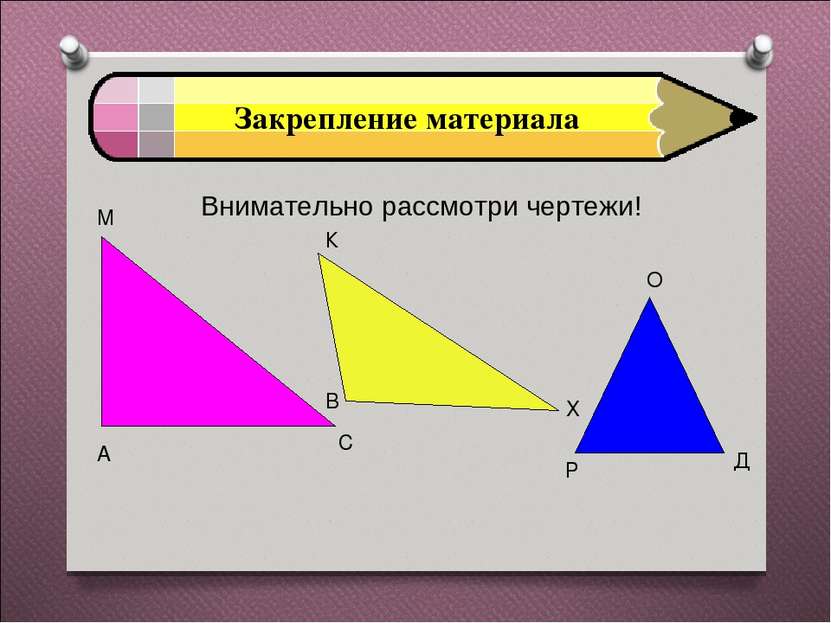
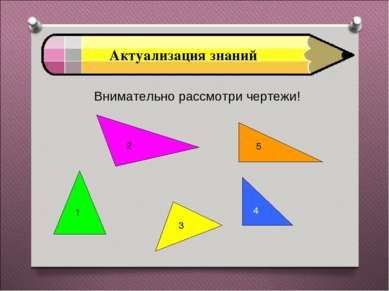
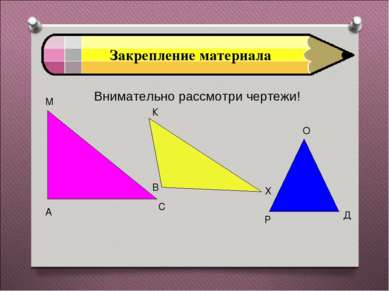
Закрепление материала Есть ли среди них равнобедренные? Если есть, то сколько? Ответ: да, один
Cлайд 21
Закрепление материала На каком месте стоит равнобедренный треугольник? Ответ: на третьем
Cлайд 22
Закрепление материала Какого он цвета? Ответ: синего
Cлайд 23
Закрепление материала Какими буквами обозначен этот треугольник? Ответ: РОД
Cлайд 24
Закрепление материала Назовите основание этого треугольника Ответ: РД
Cлайд 25
Самостоятельная работа Упр. №112, упр. №117
Cлайд 26
Решение занимательных задач 1 задача. Как с помощью спички, не разламывая ее, изобразить на столе равнобедренный треугольник?
Cлайд 27
Решение занимательных задач 2 задача. Из спичек выложите фигуру, состоящую из 9 равных треугольников, как показано на рисунке 1. Уберите 5 спичек так, чтобы осталось 5 треугольников
Cлайд 28
Контроль и рефлексия - Полностью ли реализован составленный нами план? – Соответствовала ли наша работа целям урока? - Что вы ожидали от сегодняшнего урока? - Что вызвало трудности? - Были ли задания, которые ты делал с удовольствием? - Какие знания, полученные ранее, нужны были для изучения новой темы? - А как вы считаете, знания, полученные сегодня на уроке, будут вам необходимы на следующих уроках
Cлайд 29
Домашнее задание П.18 (выучить определение равнобедренного треугольника и теорему 1), упр. №107, 111 (одно по выбору).
Cлайд 30
Литература и интернет-ресурсы Атанасян Л.С. Геометрия 7 9. М: «Просвещение», 2010 г Ляшова Н.М., .Ковалева Г.И. Открытые уроки по математике Волгоград: «Учитель»,2010 г http://www.proshkolu.ru/user/Olg-a-ndreevna/folder/123384/ http://ppt4web.ru/matematika
Cлайд 31
за урок
