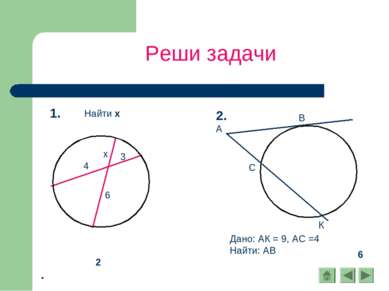
X
Код презентации скопируйте его
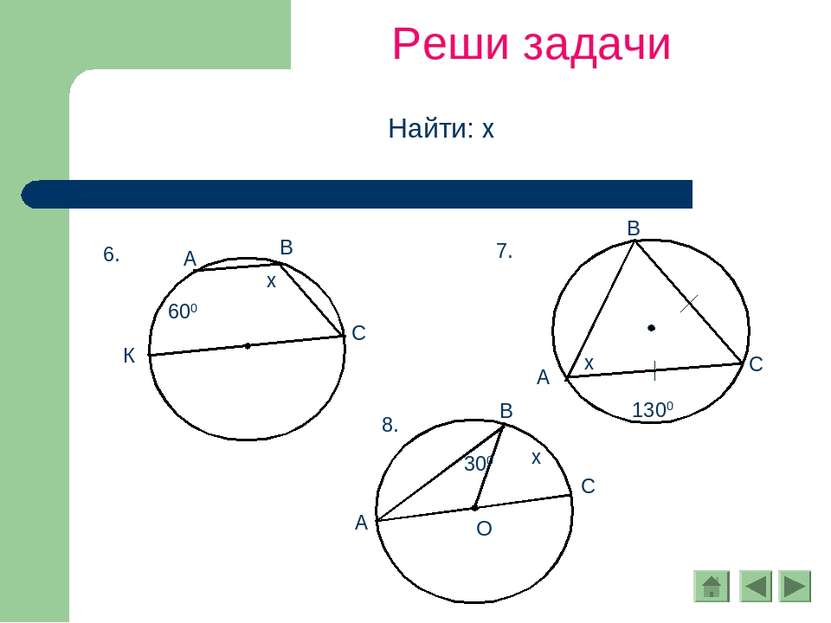
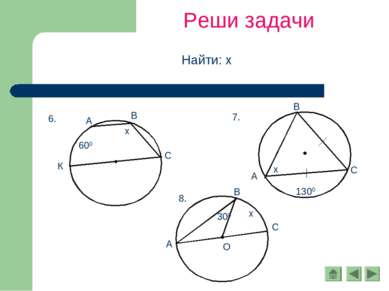
Вписанный угол
Скачать эту презентацию
Презентация на тему Вписанный угол
Скачать эту презентациюCлайд 1
Вписанный угол
Cлайд 2
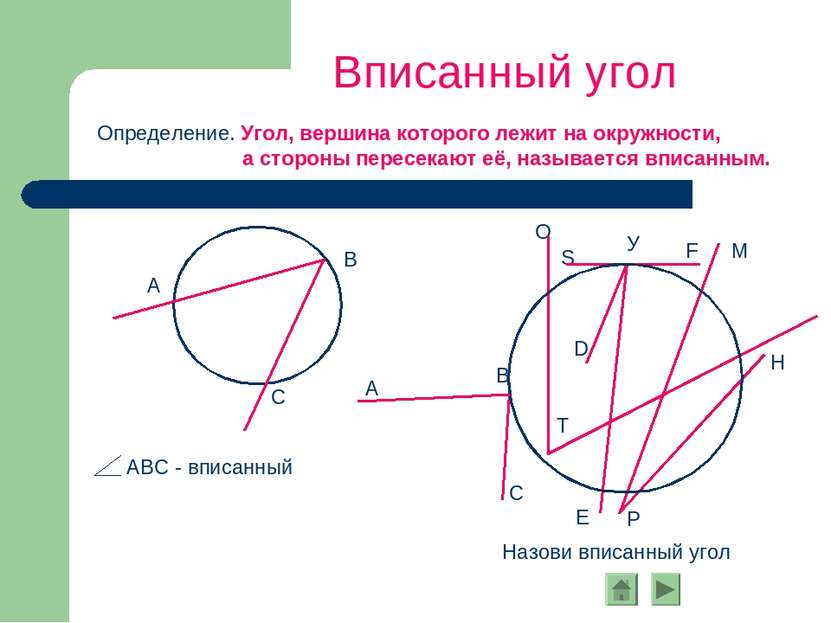
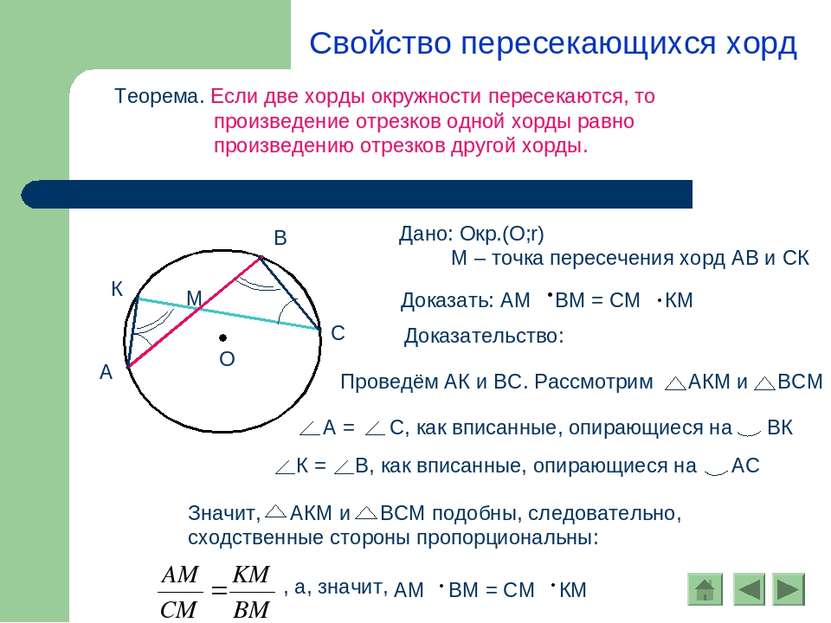
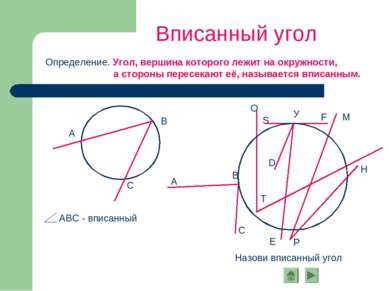Определение. Угол, вершина которого лежит на окружности, а стороны пересекают её, называется вписанным. Вписанный угол
Cлайд 3
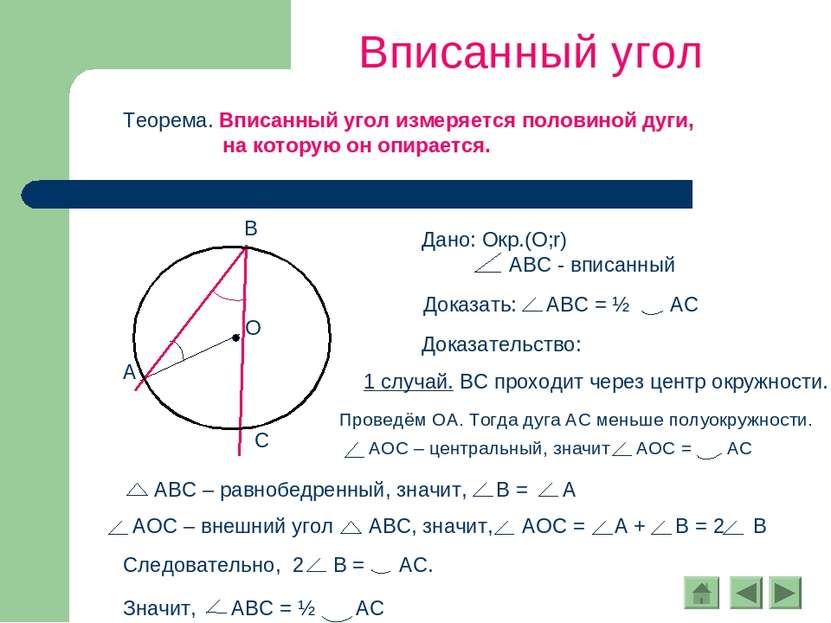
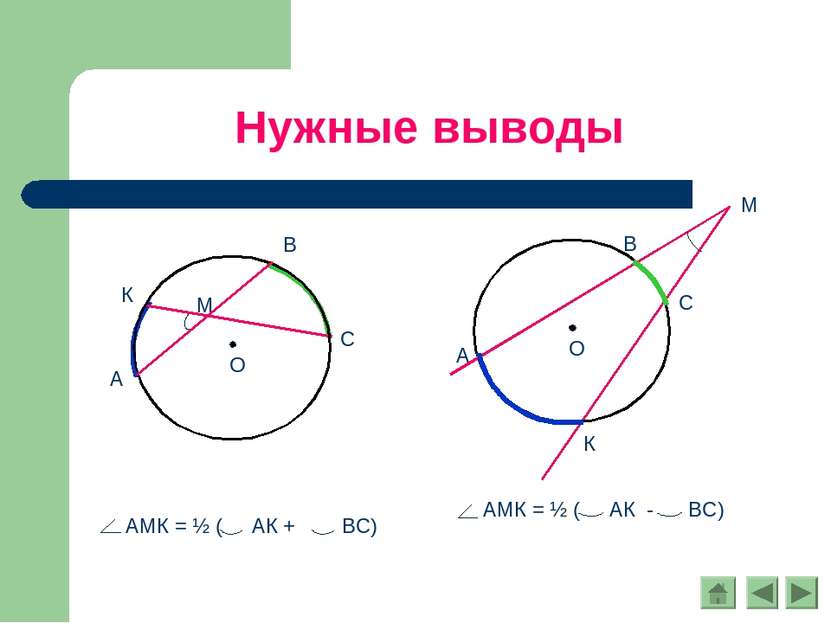
Вписанный угол Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Доказательство: 1 случай. ВС проходит через центр окружности. Проведём ОА. Тогда дуга АС меньше полуокружности.
Cлайд 4
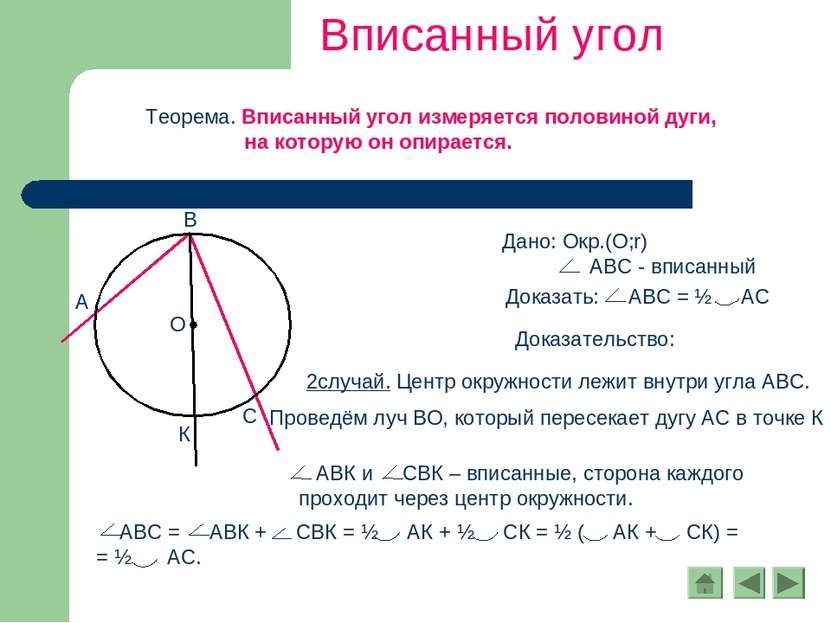
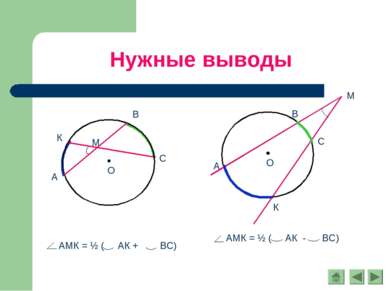
Вписанный угол Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Доказательство: 2случай. Центр окружности лежит внутри угла АВС. Проведём луч ВО, который пересекает дугу АС в точке К
Cлайд 5
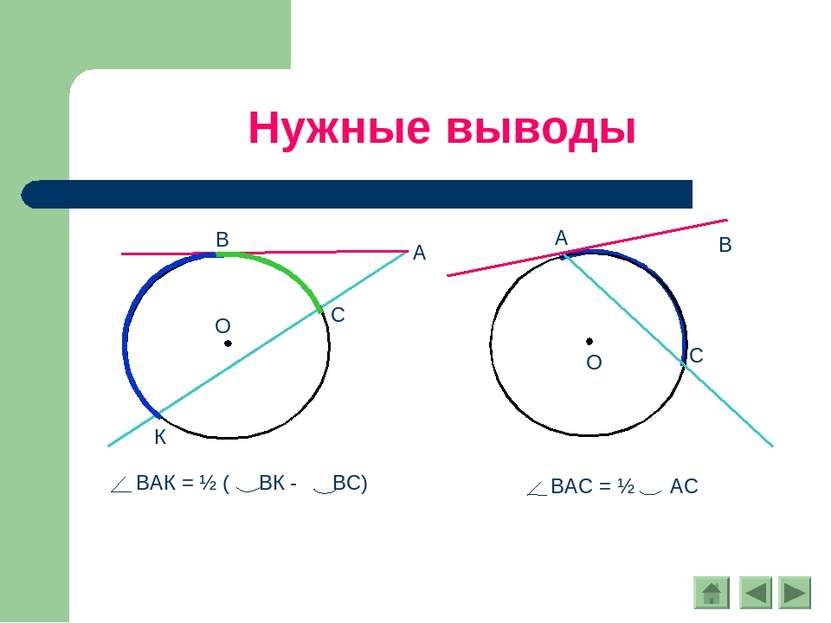
Вписанный угол Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Доказательство: 3 случай. Центр окружности лежит вне угла АВС. Проведём луч ВО, который пересекает Oкр(О;r) в точке К
Cлайд 6
Реши задачи Найти: х
Cлайд 7
Реши задачи Найти: х
Cлайд 8
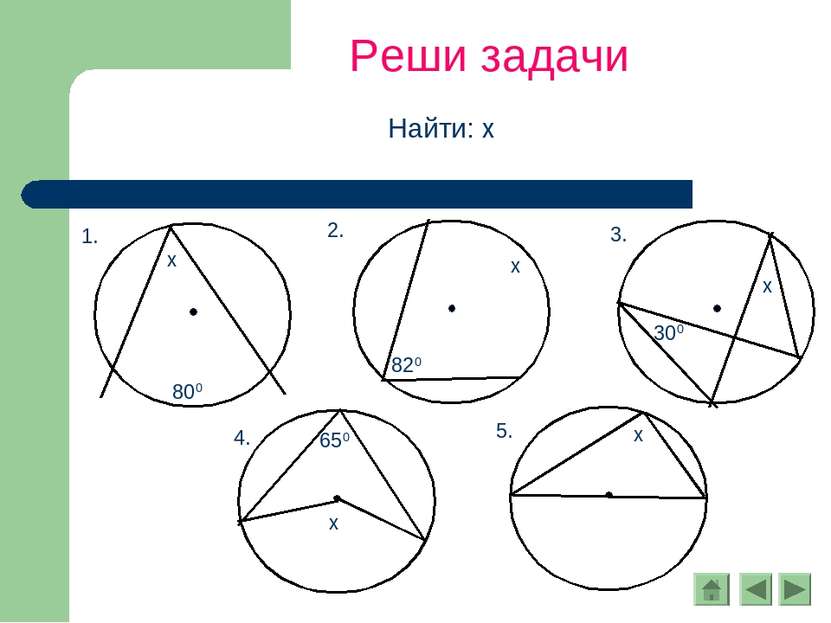
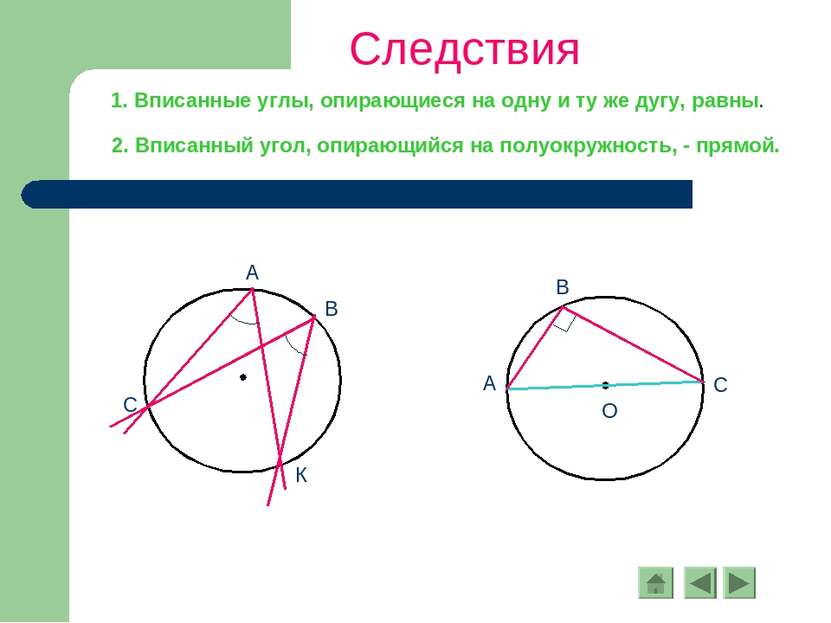
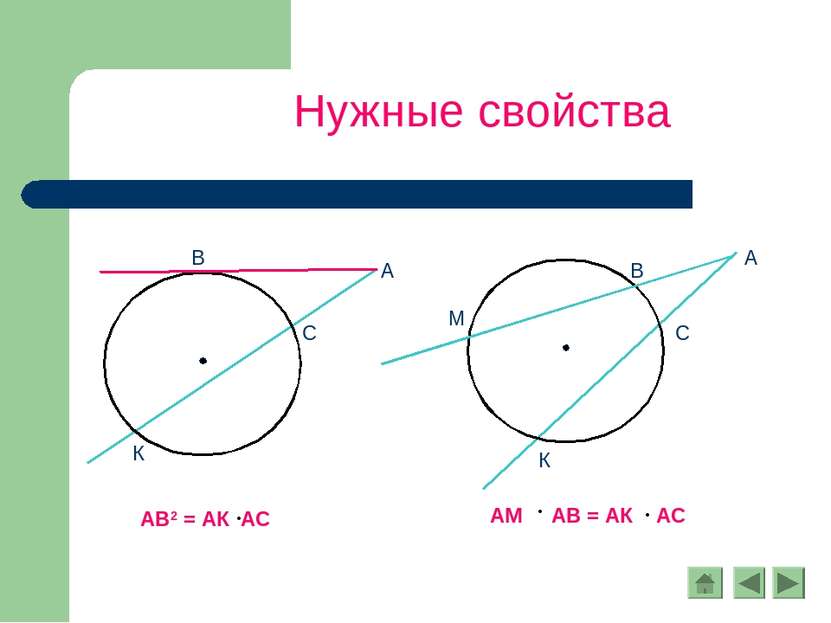
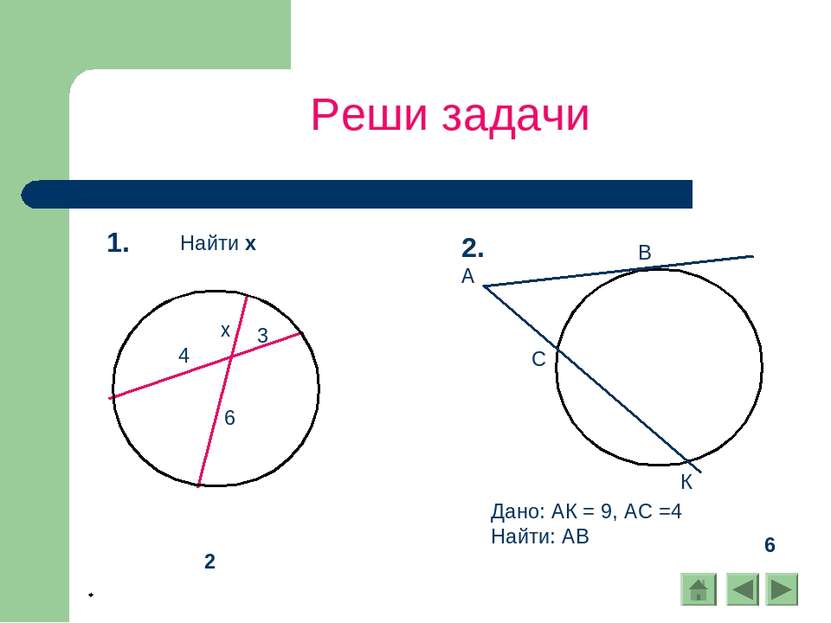
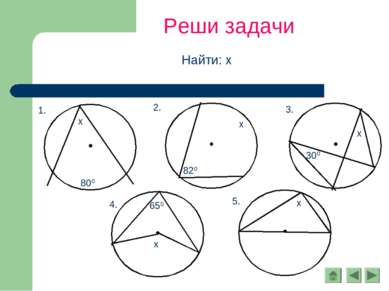
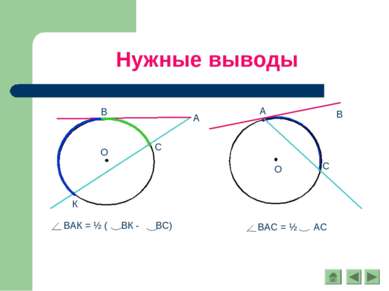
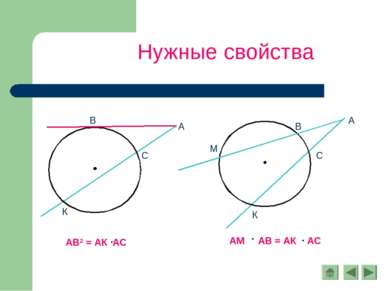
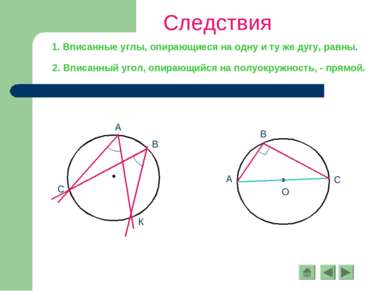Следствия 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны. 2. Вписанный угол, опирающийся на полуокружность, - прямой.
Cлайд 9
Нужные выводы
Cлайд 10
О С Нужные выводы
Cлайд 11
Свойство пересекающихся хорд Теорема. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Дано: Окр.(О;r) М – точка пересечения хорд АВ и СК Доказательство:
Cлайд 12
Нужные свойства
Cлайд 13
Реши задачи 2 С 6
Cлайд 14
Михайлова Л. П. ГОУ ЦО № 173.
