X
Код презентации скопируйте его
Сфера и шар. Объём шара и его частей
Скачать эту презентацию
Презентация на тему Сфера и шар. Объём шара и его частей
Скачать эту презентациюCлайд 1
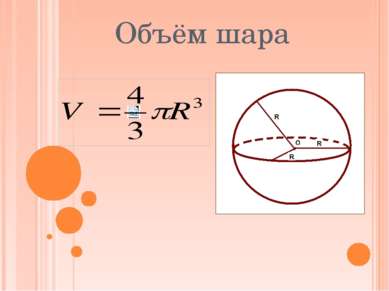
Объём шара и его частей. Учитель: Федосеева И.Н. 2015г. Сфера и шар. Уравнение сферы. МОУ «Раздольская сош» 11 класс
Cлайд 2
Основные задачи урока: Вывести формулы объёма шара и площади сферы; Показать их применение при решении задач; Познакомить учащихся с формулами для вычисления объёмов частей шара – шарового сегмента, шарового слоя и шарового сектора.
Cлайд 3
Cлайд 4
Cлайд 5
Охотничья дробь
Cлайд 6
Капля масла
Cлайд 7
Шары в архитектуре
Cлайд 8
Cлайд 9
Cлайд 10
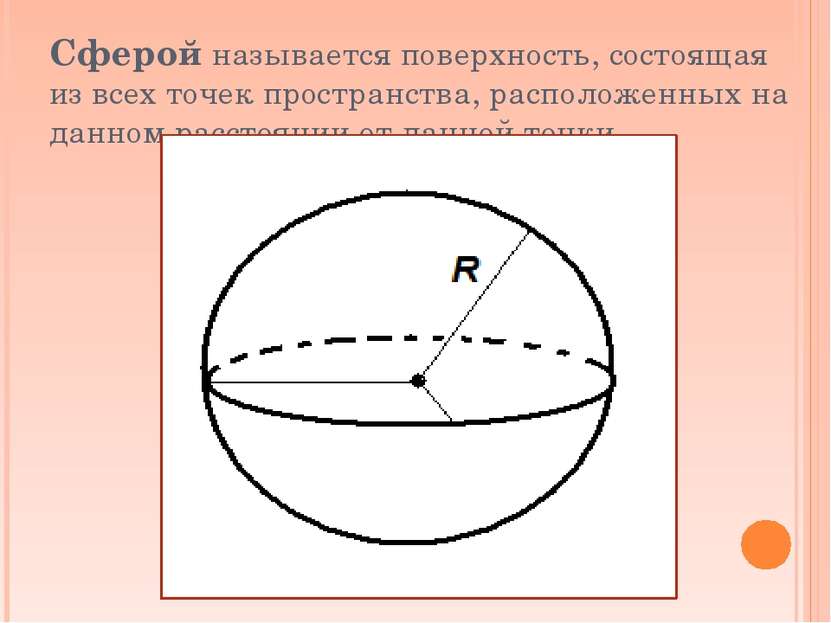
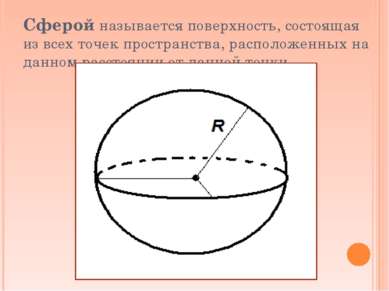Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
Cлайд 11
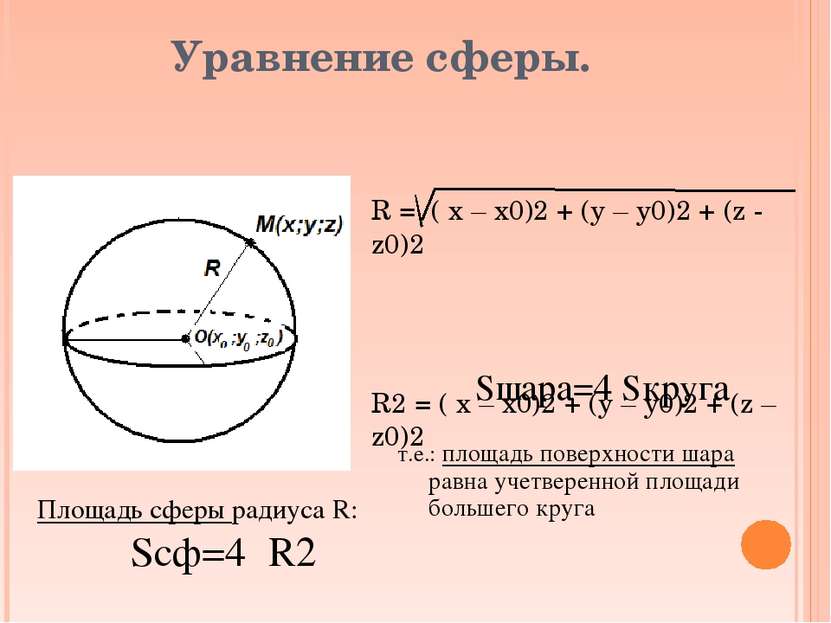
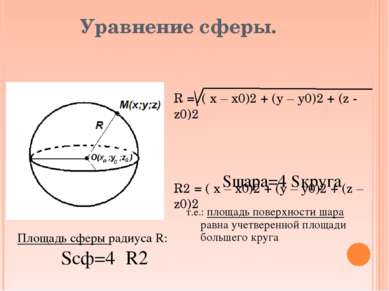Уравнение сферы. R = ( х – х0)2 + (у – у0)2 + (z - z0)2 R2 = ( х – х0)2 + (у – у0)2 + (z – z0)2 Площадь сферы радиуса R: Sсф=4πR2 Sшара=4 Sкруга т.е.: площадь поверхности шара равна учетверенной площади большего круга
Cлайд 12
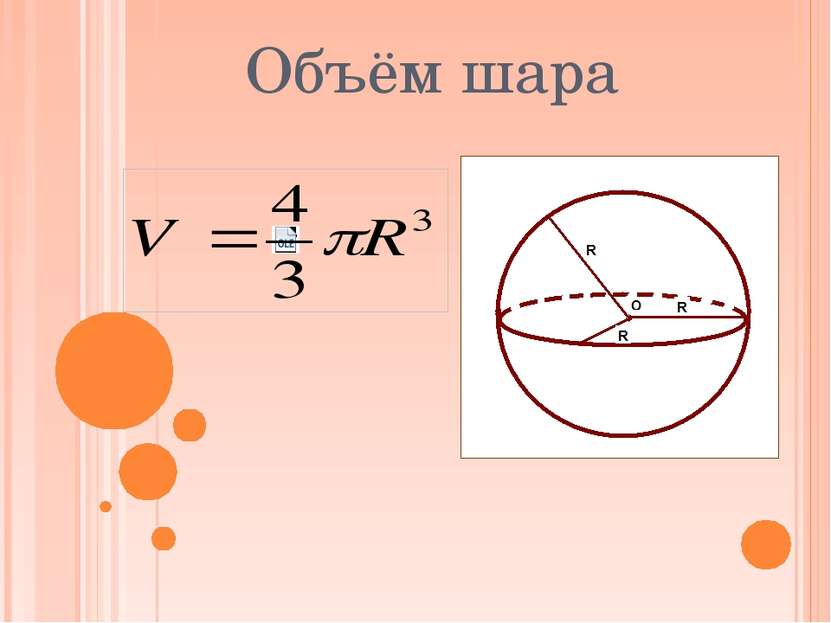
Шаром называется поверхность, состоящая из всех точек пространства, расположенных на расстоянии не больше данного от данной точки.
Cлайд 13
Объём шара
Cлайд 14
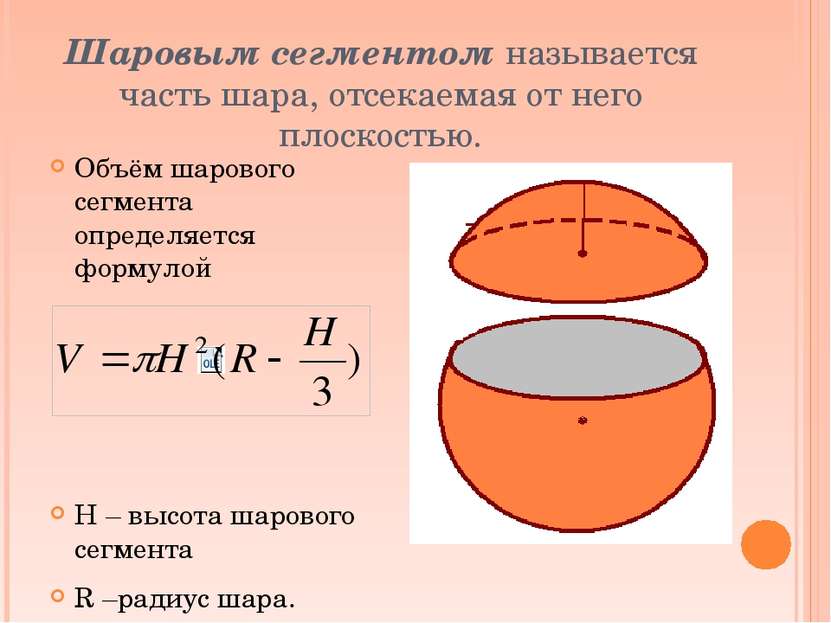
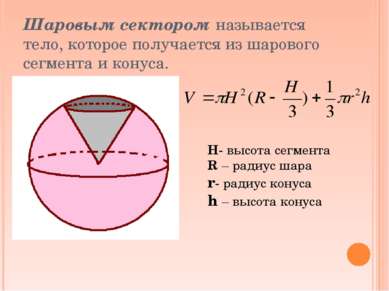
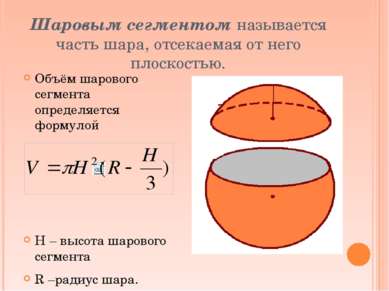Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Объём шарового сегмента определяется формулой Н – высота шарового сегмента R –радиус шара.
Cлайд 15
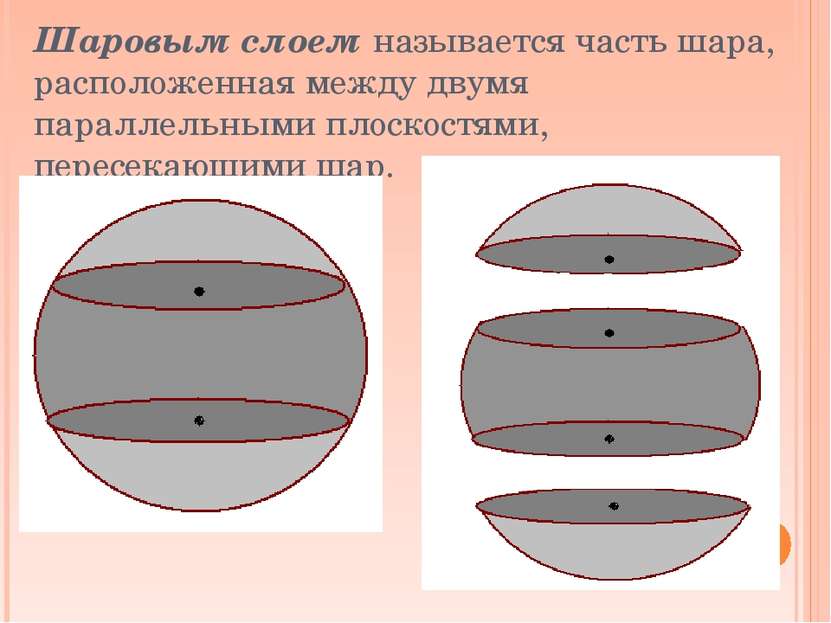
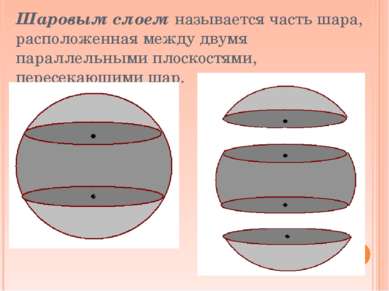Шаровым слоем называется часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар.
Cлайд 16
Шаровым сектором называется тело, которое получается из шарового сегмента и конуса. H- высота сегмента R – радиус шара r- радиус конуса h – высота конуса
Cлайд 17
Использованные материалы и литература: http://festival.1september.ru – сайт фестиваль педагогических идей. http://www.zavuch.ru/methodlib - тесты по геометрии «Геометрия 10-11» – учебник для общеобразовательных учреждений, базовый и профильный уровни. Авторы: Л.С.Атанасян и др.
