X
Код презентации скопируйте его
Волшебные десятичные дроби
Скачать эту презентацию
Презентация на тему Волшебные десятичные дроби
Скачать эту презентациюCлайд 1
проект 5 класса
Cлайд 2
ВВЕДЕНИЕ В самый обычный день после школы две лучшие подружки, ученицы пятого класса Анна и Таня делали домашнее задание по математике. Они открыли учебник и увидели десятичные дроби… Ничего не понимаю! Что такое? Эти … как их … а … десятичные дроби. Мы их не проходили! – возмутилась Таня. Реши задачу с десятичными дробями – читает Анна. – Весной засеяли 0,9 поля, а собрали урожай только с 0,6 поля. Сколько урожая с поля не собрали?
Cлайд 3
Всё таки засеяли 0 или 9? – спросила Таня. Может быть надо к 0 прибавить 9? – предложила Анна. Нет, наверно, мы должны сами выбрать 0 или 9! Анна согласилась. И только хотели девочки это записать, как учебники начали плясать и запели: Десятичные дроби Нам уж очень нужны. Что за буквочка кривая? Или это запятая? Но при чём тут запятая, Нам расскажет фея Майя!
Cлайд 4
Тут появилась фея! Прошу в моё королевство! Я узнала, что вы не знаете, что такое дроби десятичные? А побывав в моих замках, вы узнаете всё о десятичных дробях. Мы согласны! – хором сказали девочки и оказались в королевстве.
Cлайд 5
Королевство десятичных дробей 1 – ый замок, в котором вас познакомят с историей десятичных дробей 2 – ой замок, в котором вы узнаете интересные факты c десятичными дробями 3 –ий замок, в котором вас научат выполнять действия с десятичными дробями 4-ый замок, где вы встретитесь с увлекательными задачами, в которых есть десятичные дроби 5 – ый замок, в где вам расскажут сказку про десятичные дроби Выход из королевства
Cлайд 6
Из истории десятичных дробей Появились десятичные дроби в трудах арабских математиков в средние века и независимо от них в древнем Китае. Но и раньше, в древнем Вавилоне, использовали дроби такого же типа, но конечно шестидесятеричные. Позднее учёный Гартман Бейер (1563-1625) Выпустил сочинение «Десятичная логистика» где писал: «…я обратил внимание на то, что техники и ремесленники, когда измеряют какую-нибудь длину, то очень редко и лишь в исключительных случаях выражают её в целых числах одного наименования; обыкновенно им приходится или брать мелкие меры, или обращаться к дробям, точно так же астрономы измеряют величины не только в градусах, но и в долях градуса, т.е. минутах, секундах и т.п., но мне кажется их деление на 60 частей не так удобно, как деление на 10, на 100 частей и т.д., потому что в последнем случае гораздо легче складывать, вычитать и вообще производить арифметические действия; мне кажется, что десятичные доли, если бы ввести вместо шестидесятеричных, пригодились бы не только для астрономии, но и для всякого рода вычислений.» В европейскую же практику десятичные дроби ввёл Симон Стевин. До тех пор каждый, кто сталкивался с нецелыми числами, должен был возится с числителями и знаменателями.
Cлайд 7
Из истории десятичных дробей Почему же люди перешли от обыкновенных дробей к десятичным? Да потому, что действия с ними более простые, особенно сложение и вычитание. Сложим дроби 3/50 и 7/40. Сначала нужно найти наименьшее общее кратное их знаменателей (это число 200), потом разделить его на 50 и результат (число 4) умножить на числитель и на знаменатель первой дроби. Получается 12/200. Потом надо разделить 200 на 40 и частное (число 5) умножить на числитель и знаменатель второй дроби. Получается 35/200. Мы привели дроби к общему знаменателю. Только теперь мы можем сложить числители и получить ответ: 47/200. А если эти дроби представить в виде десятичной записи: 3/50=0,06; 7/40=0,175, сумма находится мгновенно – это 0,235. Конечно же, число 1/7 приходится записывать лишь с некоторой точностью, 0,143 или 0,14287, но ведь в жизни всё имеет свои пределы точности. Лишь в первой четверти 18 в. дробные числа стали записывать с помощью простой десятичной точки. В некоторых странах, и в частности в России, вместо точки используют запятую. Её ввёл немецкий математик Георг Андреас Бёклер в 1661 г.
Cлайд 8
Из истории десятичных дробей Сегодня мы пользуемся десятичными дробями естественно и свободно. Однако то, что кажется естественным нам, служило настоящим камнем преткновения для учёных Средневековья. В Западной Европе 16 в. вместе с широко распространённой десятичной системы представления целых чисел в расчётах повсюду применялись шестидесятеричные дроби, восходящие ещё к древней традиции вавилонян. Понадобился светлый ум нидерландского математика Симона Стевина, чтобы привести запись и целых, и дробных чисел в единую систему. По-видимому, толчком создания десятичных дробей послужили составленные им таблицы сложных процентов. В 1585 г. он опубликовал книгу «Десятина», в которой объяснил десятичные дроби. Обозначения Стевина не отличались совершенством, так же как и обозначения его коллег и последователей. Вот как бы они записали число 3,1415:
Cлайд 9
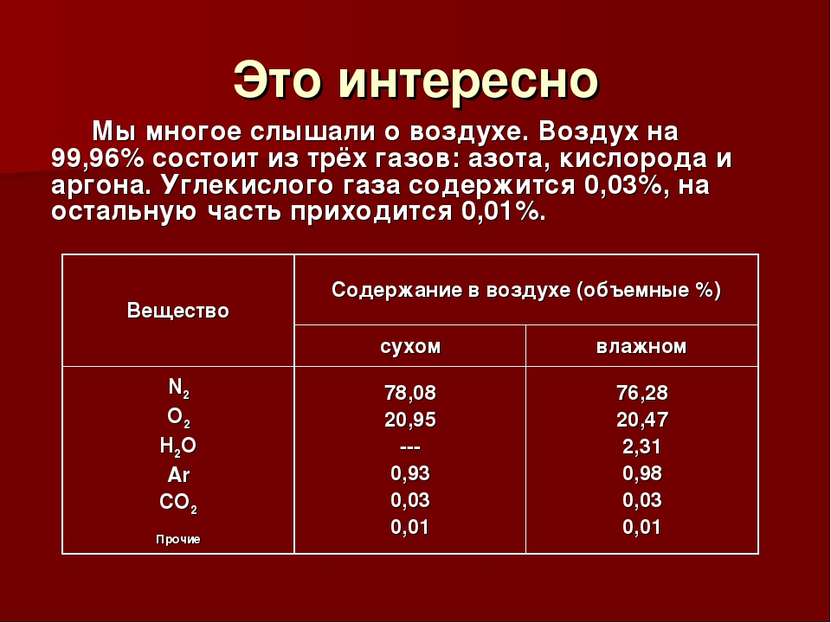
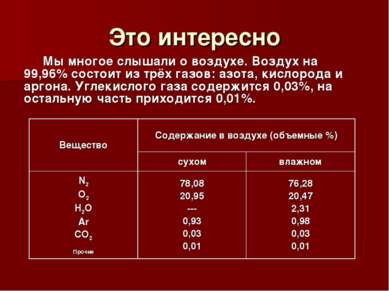Это интересно Мы многое слышали о воздухе. Воздух на 99,96% состоит из трёх газов: азота, кислорода и аргона. Углекислого газа содержится 0,03%, на остальную часть приходится 0,01%. Вещество Содержание в воздухе (объемные %) сухом влажном N2 O2 H2O Ar CO2 Прочие 78,08 20,95 --- 0,93 0,03 0,01 76,28 20,47 2,31 0,98 0,03 0,01
Cлайд 10
Это интересно Огромное значение для познания мира имеет проблема численного соотношения между атомами различных элементов. Если сравнить имеющееся на всей Земле, железо, кобальт и никель, то окажется, что земной шар состоит из: Железа на 92% Кобальта на 0,5% Никеля на 7,5 % Точнейшие химические анализы огромного числа метеоритов, упавших на Землю дали замечательные результаты. Выяснилось, что в железных метеоритах процентное содержание железа, кобальта и никеля поразительно совпадает с содержанием их на нашей планете.
Cлайд 11
Стих о десятичных дробях Рассказать мне можно много, О том, что такое десятичные дроби, О том, что можно в конце дробной части, Справа отбросить иль вставить нули. Ну а как их сравнить, ты мне расскажи. Ну, это, конечно же, проще простого. Сравни целые части десятичной ты дроби, И та, у которой она будет больше, Конечно же, будет и больше. Ну, если те части как раз и равны, То, что же мне делать, ты подскажи. Если у двух десятичных дробей целые части равны, Ты на первый из несовпадающих разрядов смотри, И тот, у которой он будет больше, конечно же, будет и больше. Всё ли запомнил, ты мне скажи? Как сложить и вычесть ?. Запомни алгоритм сложения или вычитания десятичных дробей. Для начала число знаков после запятой, ты уравняй, Запиши их в столбик и конечно, знай, Что запятая должна оказаться под запятой, А потом только и решай. Сначала выполни сложение или вычитание, Не обращая на запятую никакого внимания. Ну, в ответе, ты, конечно же, поставь запятую под запятой в данных дробях. Ты запомни эти правила навсегда, чтобы в памяти твоей, они остались, как дважды два!
Cлайд 12
Задача 1 Вася нашёл в реке затонувшие сокровища и принёс их домой. Он решил продать их богачу. Но богач обманул его на 1234567 рублей. Сколько стоят сокровища в действительности, если 0,5 грамма сокровищ стоит 120,5 $,а их вес 564,67 граммов?
Cлайд 13
Задача 2 Гусеница бабочки-капустницы съедает за месяц 10г. капусты. Синица съедает ежедневно 100 гусениц. Подсчитайте, сколько капусты "экономит" за 1 месяц (30 дней) семья синиц состоящая из самки, самца и 4 птенцов, если считать, что птенец съедает в 2 раза меньше взрослой синицы.
Cлайд 14
Задача 3 Коля мечтал о шоколадке, длина которой 3,7 м., а ширина 2,1 м. Толя мечтал о шоколадке такой же длины, но втрое больше площадью, чем у Коли. На сколько метров ширина шоколадки о которой мечтал Толя длиннее ширины о которой мечтал Коля?
Cлайд 15
Задача 4 На пустой ёмкости сохранилась надпись: БРУТТО — 21,8 кг, НЕТТО — 20,6 кг. В неё положили 19,9кг масла. Что теперь нужно написать на ёмкости?
Cлайд 16
Задача 5 Утка Донна Дак решила приготовить яблочный пирог. Для этого она взяла: 0,57 кг яблок, 2 стакана муки по 0,25 кг, 0,01 кг сливочного масла, 2 стакана молока и 2 яйца. Сколько будет весить пирог, когда Донна Дак вытащит его из духовки? Сколько будет весить пирог, когда племянники Донны Дак съедят 1/3 пирога?
Cлайд 17
Хотите узнать цены на основные продукты в Нарьян-Маре? (руб. за кг)
Cлайд 18
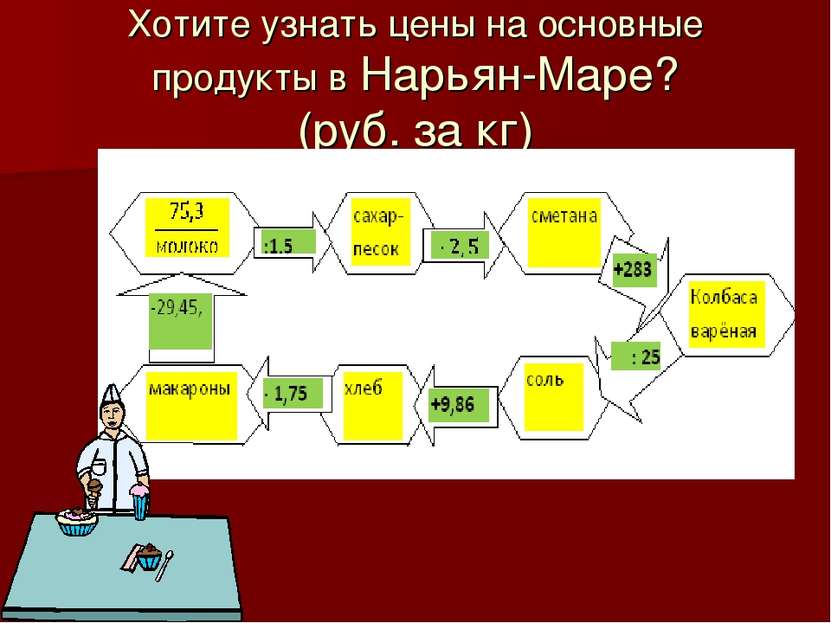
Цены в Нарьян-Маре в 2012 г. Молоко – 75,3 рубля Сахар 50,2 рубля Сметана 125,5 рубля колбаса варёная 408,5 соль 16,34 рубля хлеб 26,2 рубля макароны 45,85 рубля
Cлайд 19
Эти и многие другие задачи вы можете встретить в сборнике задач, выпущенным 5 классом!
Cлайд 20
Откуда появились десятичные дроби? В городе, где жили дроби, такие как 1 2/10, 2 98/100, 1872/10000, 5/100 и вообще со знаменателями 10, 100, 1000 и т.д., все жили очень дружно. Никто никого не бил, не обижал и никто не спорил. В этом городе были красивые дома, а на окошках стояли красивые цветочки. У каждой дроби был свой дом и сад. В саду росли наливные яблочки, вишенки, груши, а ещё разные цветочки. Были там также и школы. Туда ходили маленькие дробики такие со знаменателем 10. Были и взрослые дроби со знаменателями от 100 до 100 000 и совсем старые со знаменателем от 100 000 и до бесконечности. Взрослые дроби бегали на работу.
Cлайд 21
Ну, а старики и старушки весь день сидели в креслах-качалках и читали книги, а иногда шлепали по попкам дробей-малышей за непослушание или шалости, или читали им сказки Но однажды на город напал Штрих со своей армией. Он беспощадно убивал всех, сжигал дома, грабил их. Десять лет длилась война. Побеждали то одни, то другие, но выиграть войну никто не мог. Но один добрый Волшебник помог беспомощным дробям. Он погасил горящие дома, вернул награбленное и прогнал штриха прочь. Лишь один вопрос волновал Волшебника: «Как же вылечить пораненные дроби?». Он долго думал, и наконец, придумал. Вместо дробной черты он дал дробям запятые, убрал знаменатели, а таким дробям, как 1/100, 32/1000 и т.д. добавил после целой части справа 1, 2, 3 и т.д. нулей, смотря сколько их было в знаменателе.
Cлайд 22
Вот и окончилось путешествие девочек по королевству десятичных дробей. В этом путешествии они узнали очень много нового, и теперь любая задачка с десятичными дробями им по плечу!
