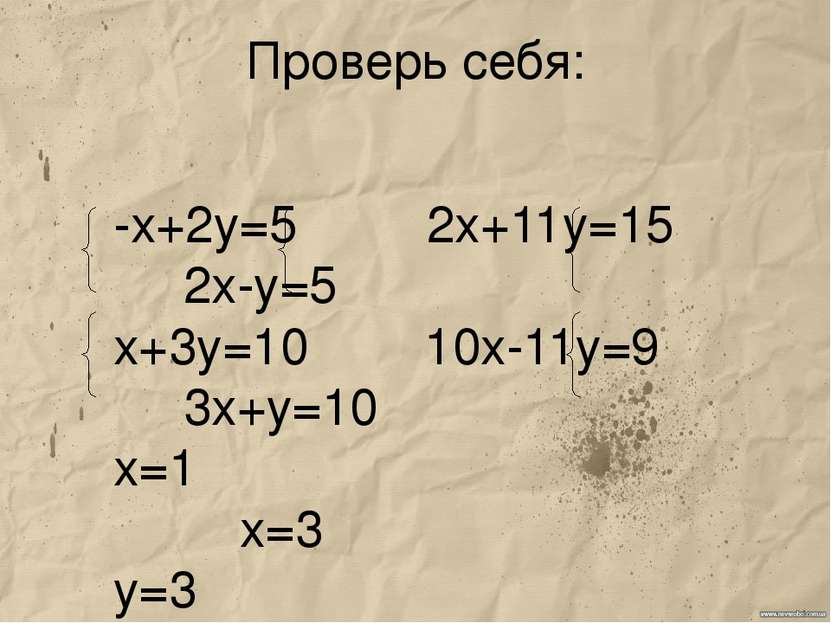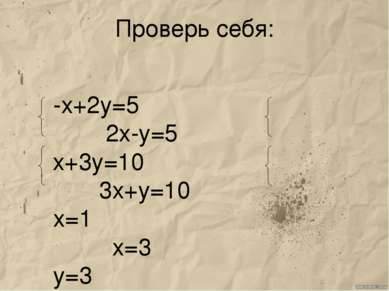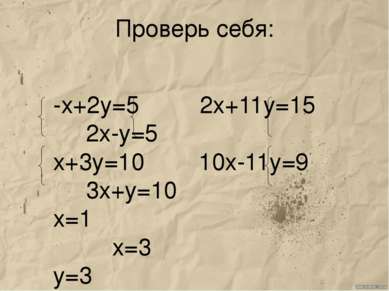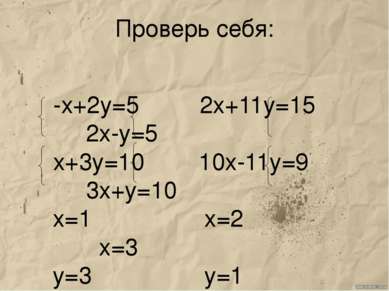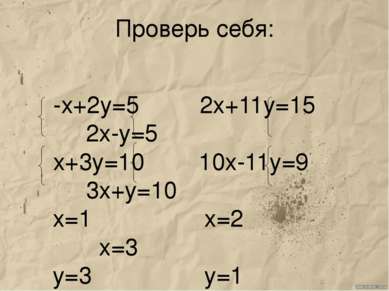X
Код презентации скопируйте его
Решение систем двух уравнений с двумя переменными способом сложения
Скачать эту презентацию
Презентация на тему Решение систем двух уравнений с двумя переменными способом сложения
Скачать эту презентациюCлайд 1
Решение систем линейных уравнений способом сложения. Работу выполнила ученица 7А класса МОБУСОШ №4 Конькова Валерия Учитель: О.К. Ермишко.
Cлайд 2
При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.
Cлайд 3
Пример № 1 Решим систему уравнений: 2х+11у=15, 10х-11у=9 11у и 11у противоположны и равно 0. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 12х=24. Заменим одно из уравнений системы (1), например первое, уравнением 12х=24, получим систему: 12х=24, 2х+11у=15 Система (2) равносильна системе (1).Решим систему (2).Из уравнения 12х=24, находим ,что х=2. Подставим значения х в уравнение: 2х+11у=15, получим уравнение с переменной у: 2*2+11у=15 Решим это уравнение: х=2 х=2 4+11у=15 у=1 Пара (2;1) - решение системы (2) а значит, и данной системы (1).
Cлайд 4
Пример №2 Решим систему уравнений: 40х+3у=10, 20х-7у=5 Почленное сложение уравнений системы не приведёт к исключению одной из переменных. Однако если умножить все члены второго уравнения на -2, а первое уравнение оставить без изменений, то коэффициенты при х в полученных уравнениях будут противоположными числами: 40х+3у=10 -40х+14у=-10 Теперь почленное сложение приводит к уравнению с одной переменной 17у=0. Из этого уравнения находим, что у=0. Подставим в первое уравнение вместо у число 0, найдём значение х: у=0 у=0 40х+3*0=10 х=0,25 Ответ:х=0,25, у=0 (0,25;0).
Cлайд 5
Пример № 3 Решим систему уравнений: 3х+5у=10 4х-2у=9 Подберём множители к уравнениям системы так, чтобы после умножения на них коэффициенты при х стали противоположными числами. Умножив первое уравнение системы на -4, а второе на 3, получим: -12х-20у=-40 12х-6у=27 Отсюда найдём, что: -26у=-13 у=0,5 Подставим значение у в уравнение -12х-20у=-40, найдём, что х равен 2,5 Ответ: х=2,5, у=0,5 (2,5;0,5)
Cлайд 6
Мы рассмотрели примеры решения систем с помощью сложения. При решении двух линейных уравнений с двумя переменными способом сложения поступают следующим образом: Умножают почленно уравнение системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами; Складывают почленно левые и правые части уравнений системы; Решают получившееся уравнение с одной переменной; Находят соответствующее значение второй переменной.
Cлайд 7
Проверь себя: -х+2у=5 х+3у=10
Cлайд 8
Проверь себя: -х+2у=5 х+3у=10 х=1 у=3
Cлайд 9
Проверь себя: -х+2у=5 2х-у=5 х+3у=10 3х+у=10 х=1 у=3
Cлайд 10
Проверь себя: -х+2у=5 2х-у=5 х+3у=10 3х+у=10 х=1 х=3 у=3 у=1
Cлайд 11
Проверь себя: -х+2у=5 2х+11у=15 2х-у=5 х+3у=10 10х-11у=9 3х+у=10 х=1 х=3 у=3 у=1
Cлайд 12
Проверь себя: -х+2у=5 2х+11у=15 2х-у=5 х+3у=10 10х-11у=9 3х+у=10 х=1 х=2 х=3 у=3 у=1 у=1
Cлайд 13
Проверь себя: -х+2у=5 2х+11у=15 2х-у=5 х+3у=10 10х-11у=9 3х+у=10 х=1 х=2 х=3 у=3 у=1 у=1 Молодец !!!
Cлайд 14
Использованная литература: Учебник: Алгебра. 7 класс: учеб. для общеобразоват. учреждений / (Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова); под ред. С.А.Теляковского. – 19-е изд. – М. : Просвещение, 2010. – 240 с.
