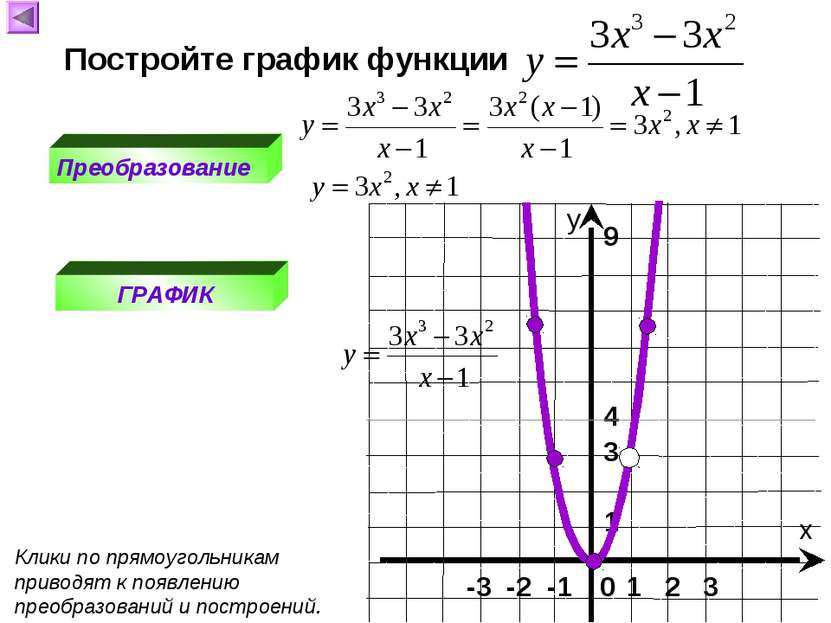
X
Код презентации скопируйте его
Функция у=ах^2, её свойства и график
Скачать эту презентацию
Презентация на тему Функция у=ах^2, её свойства и график
Скачать эту презентациюCлайд 1
Функция у=кх² , её свойства и график. 8 класс учебник Мордковича А. Г. Ткаченко И. В. гимназия №5 г. Мурманск
Cлайд 2
Cлайд 3
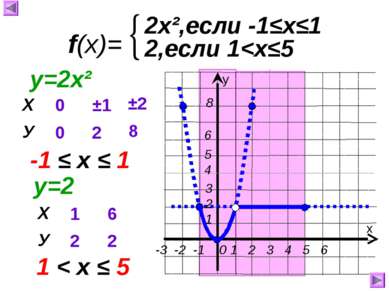
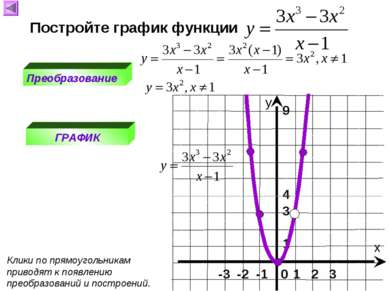
0 0 1 1 2 4 3 9 -1 1 -2 4 -3 9 у=х² 1 2 3 0 -3 -2 -1 1 9 4 Ось симметрии Графиком является парабола. Вершина параболы Ветвь параболы Ветвь параболы Ветви направлены вверх Точка (0;0) – вершина параболы Ось у- ось симметрии Построим график функции у=х² для этого значения аргумента (х) выберем сами, а значения функции (у) вычислим по формуле у=х². х У
Cлайд 4
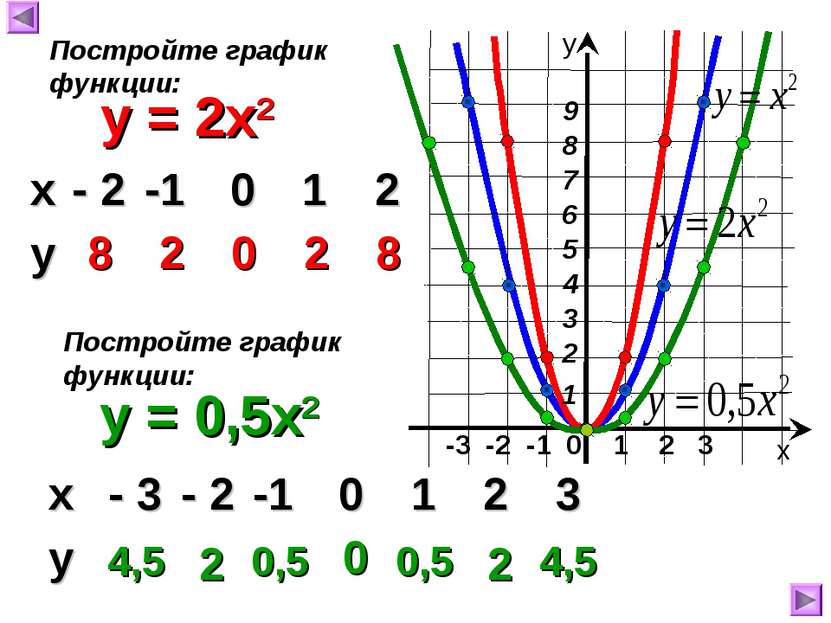
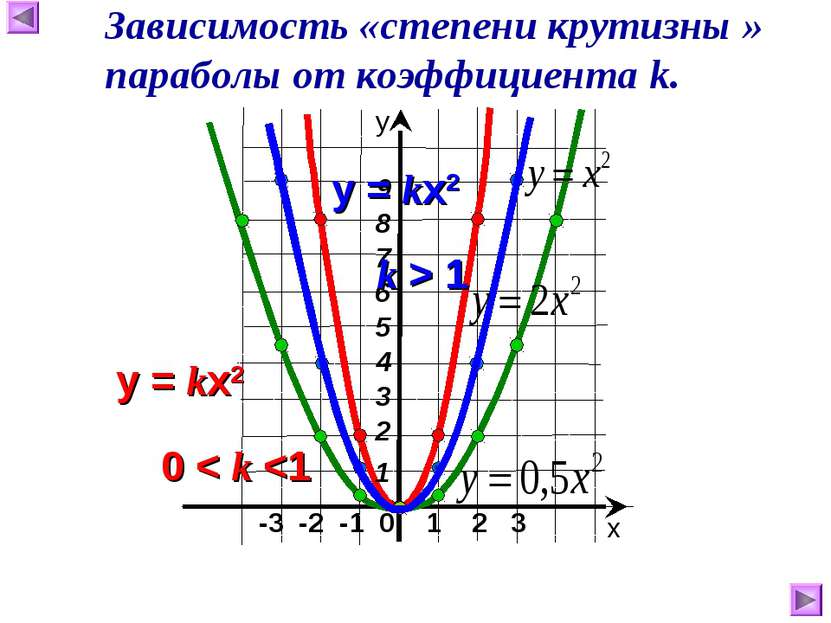
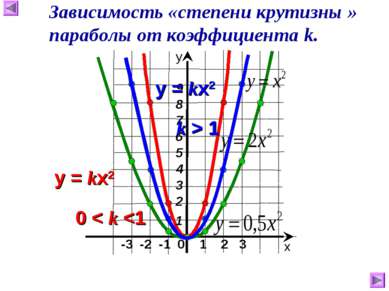
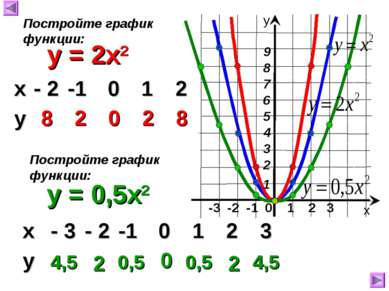-3 -2 -1 0 1 2 3 y = 2x2 8 2 0 2 8 х у Постройте график функции: y = 0,5x2 Постройте график функции: 4,5 2 0,5 0 0,5 2 4,5 х - 2 -1 0 1 2 у х - 3 - 2 -1 0 1 2 3 у
Cлайд 5
-3 -2 -1 0 1 2 3 х у Зависимость «степени крутизны » параболы от коэффициента k.
Cлайд 6
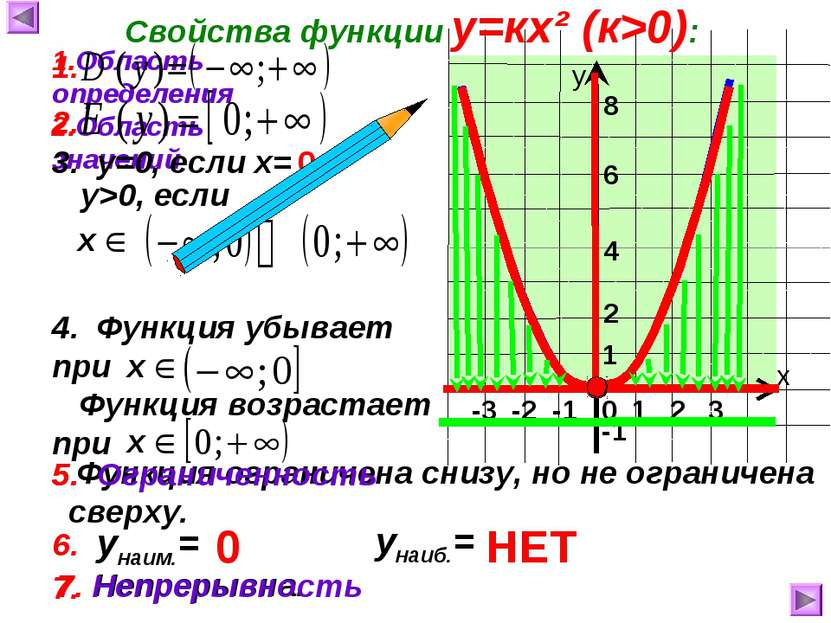
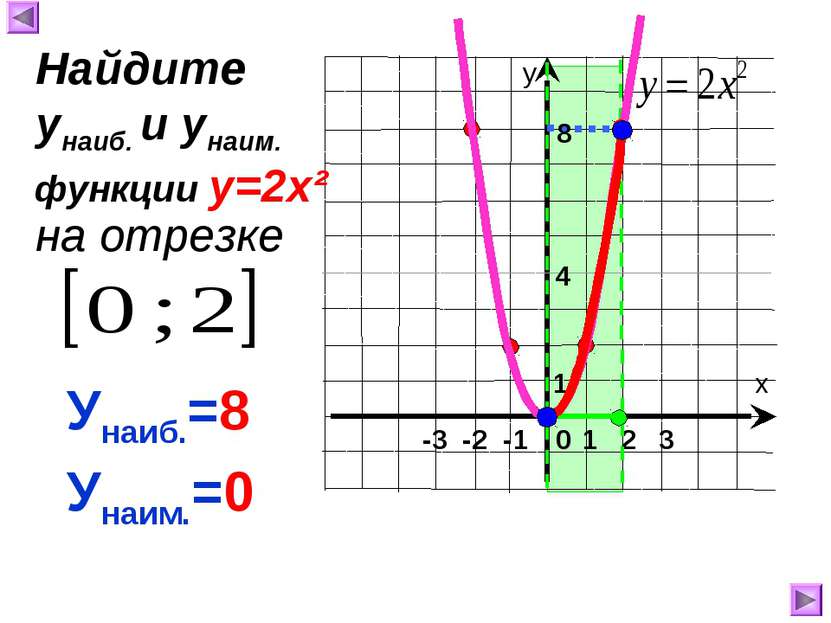
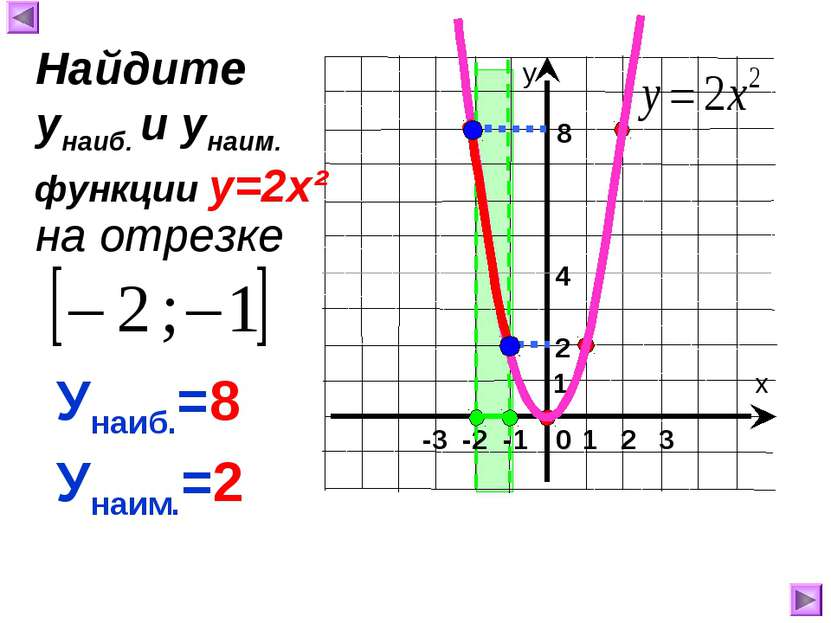
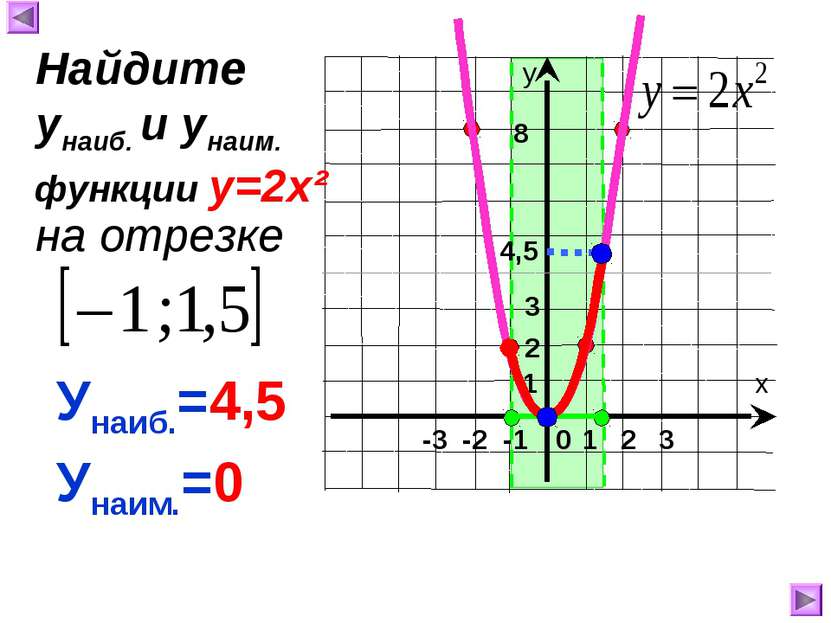
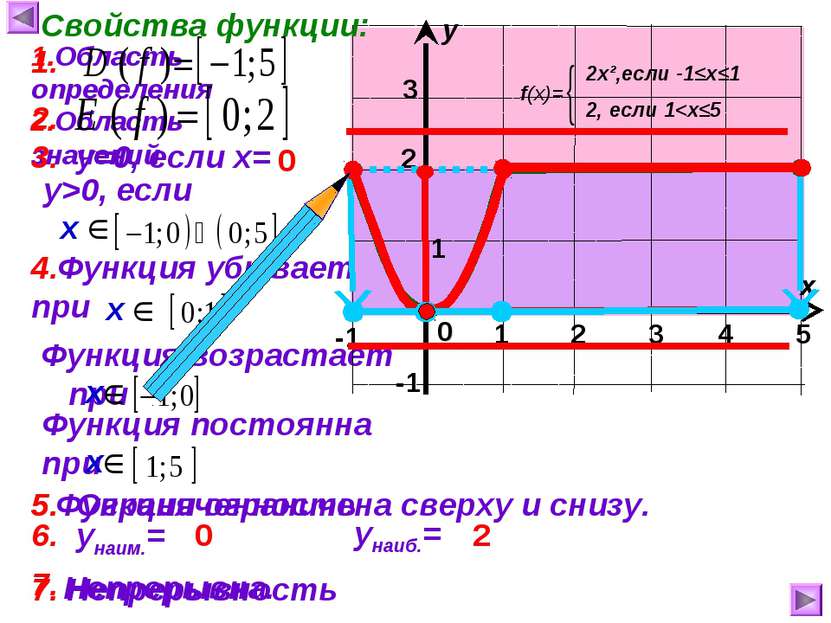
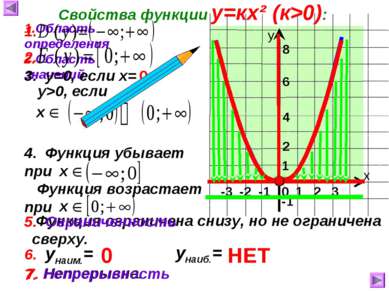7. Непрерывна. -3 -2 -1 Функция возрастает при Функция ограничена снизу, но не ограничена сверху. 1 х у 0 Свойства функции у=кх² (к>0): 1.Область определения 2 6 -1 4 2.Область значений 3. у=0, если х= 0 1 2 3 у>0, если 4. Функция убывает при 5. Ограниченность 1. 2. 5. 6. унаим.= унаиб.= НЕТ 0 7. Непрерывность 8
Cлайд 7
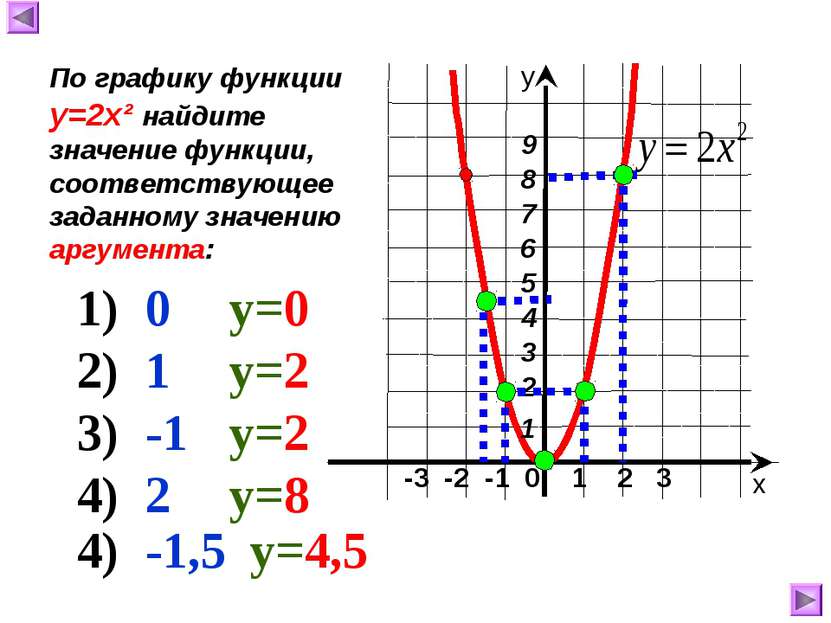
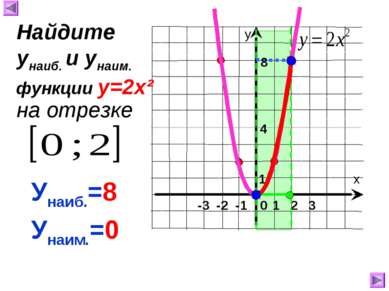
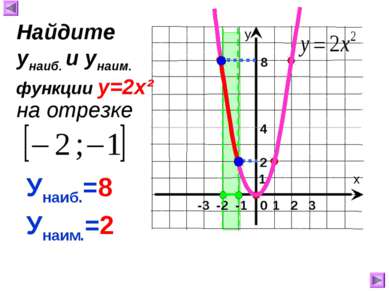
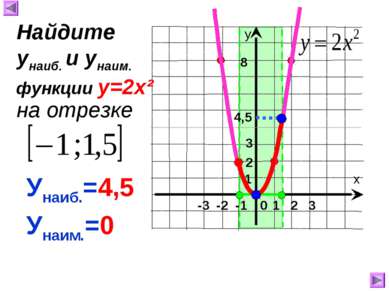
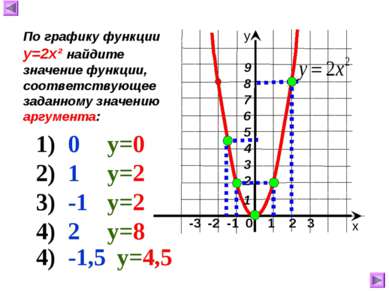-3 -2 -1 0 1 2 3 х у По графику функции у=2х² найдите значение функции, соответствующее заданному значению аргумента: 1) 0 у=0 2) 1 у=2 3) -1 у=2 4) 2 у=8 4) -1,5 у=4,5
Cлайд 8
1 8 4 Унаиб.=8 Унаим.=0 Найдите унаиб. и унаим. на отрезке функции у=2х²
Cлайд 9
1 8 4 Унаиб.=8 Унаим.=2 Найдите унаиб. и унаим. на отрезке функции у=2х² 2
Cлайд 10
1 8 4,5 Унаиб.=4,5 Унаим.=0 Найдите унаиб. и унаим. на отрезке функции у=2х² 2 3
Cлайд 11
Cлайд 12
Cлайд 13
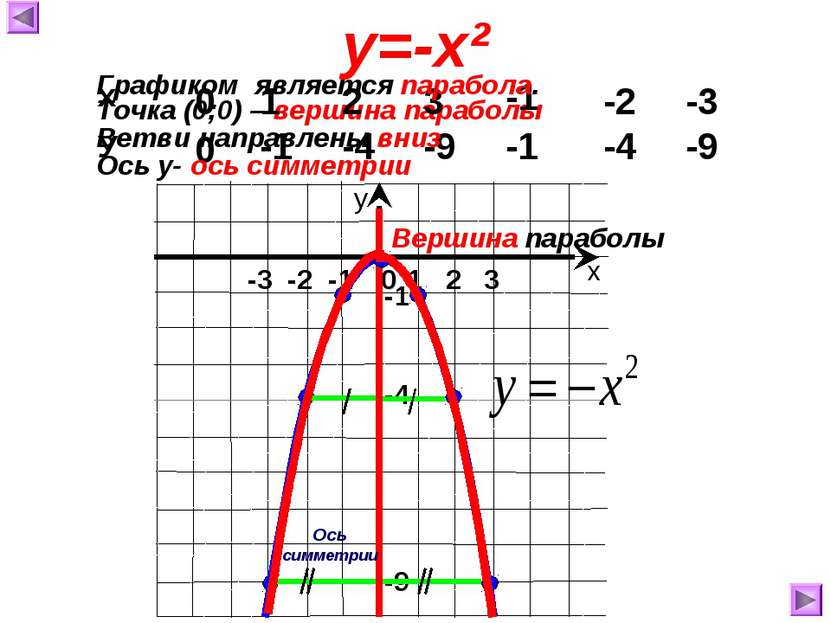
Построим график функции у=-х² для этого значения аргумента (х) выберем сами, а значения функции (у) вычислим по формуле у=-х².
Cлайд 14
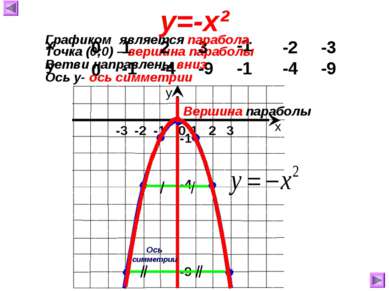Точка (0;0) – вершина параболы 0 0 1 -1 2 -4 3 -9 -1 -1 -2 -4 -3 -9 у=-х² Ось симметрии Вершина параболы Графиком является парабола. Ветви направлены вниз Ось у- ось симметрии х У
Cлайд 15
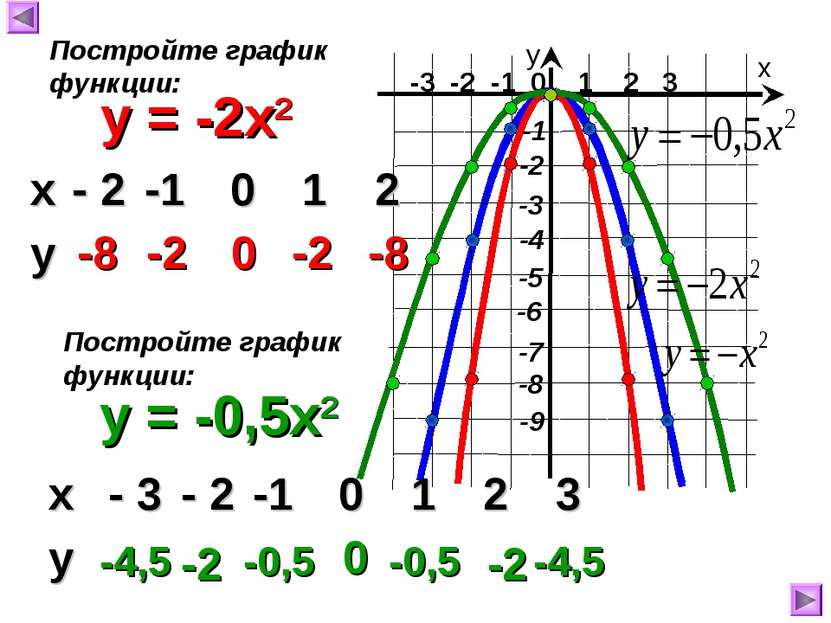
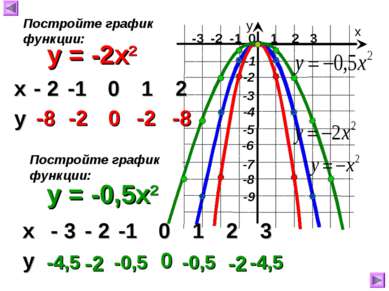-3 -2 -1 0 1 2 3 х у y = -2x2 -8 -2 0 -2 -8 Постройте график функции: y = -0,5x2 Постройте график функции: -4,5 -2 -0,5 0 -0,5 -2 -4,5 х - 2 -1 0 1 2 у х - 3 - 2 -1 0 1 2 3 у
Cлайд 16
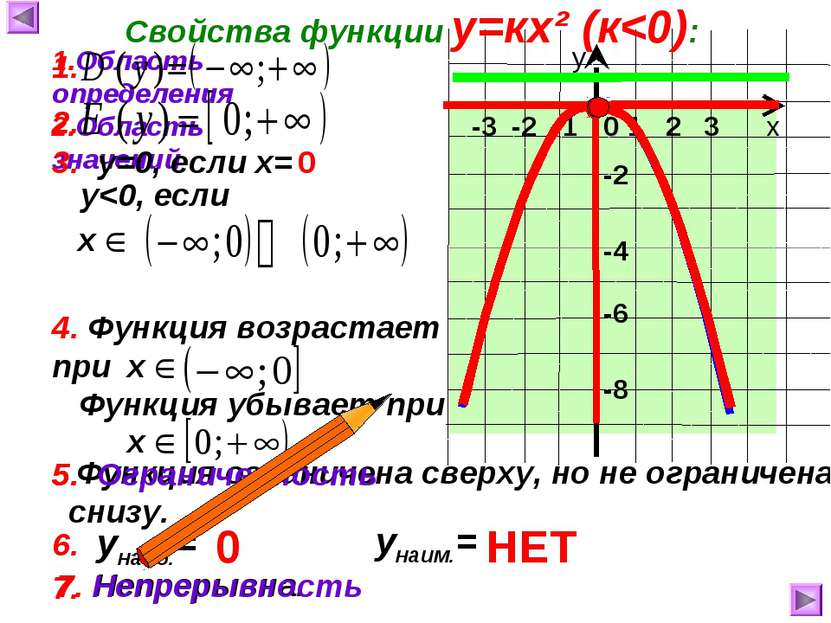
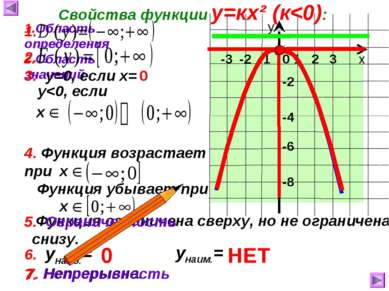7. Непрерывна. -3 -2 -1 Функция убывает при Функция ограничена сверху, но не ограничена снизу. х у 0 Свойства функции у=кх² (к
Cлайд 17
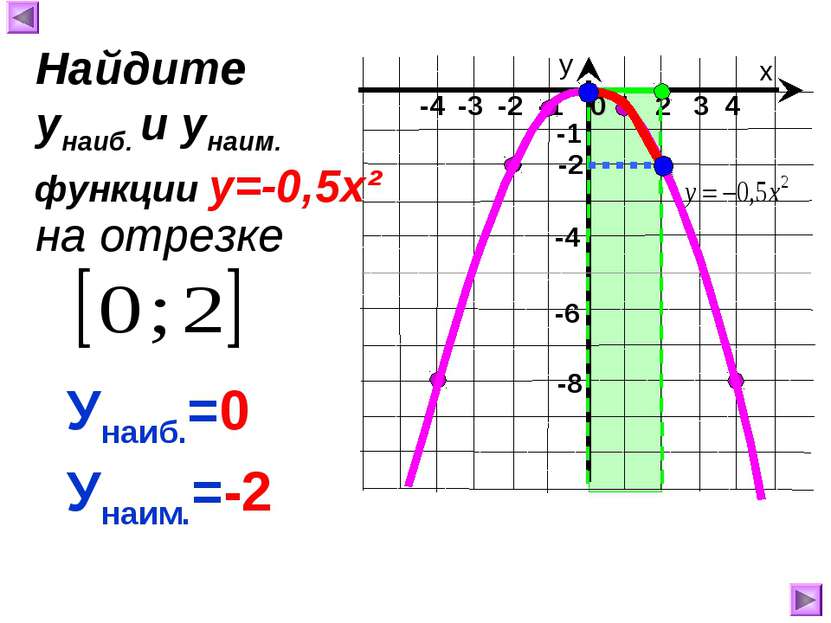
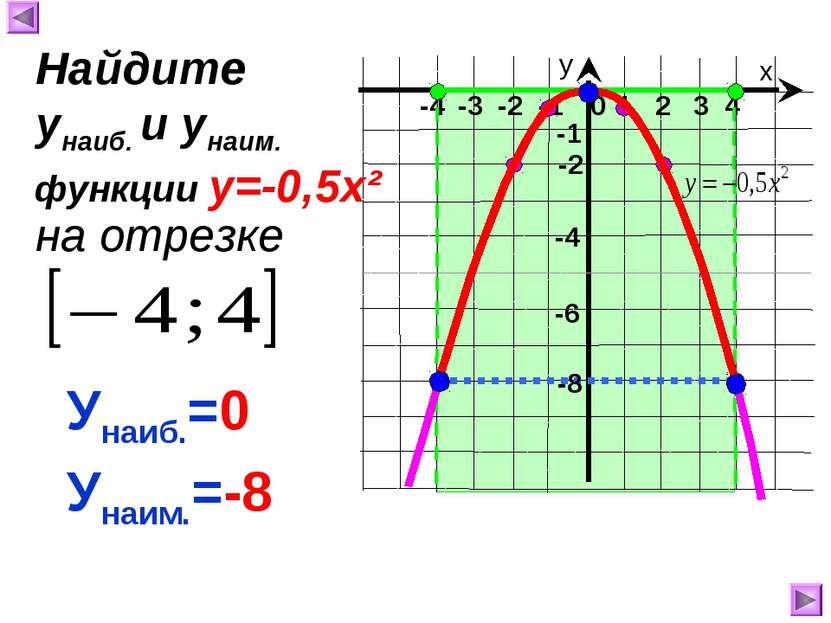
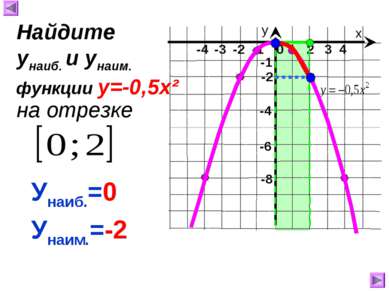х у 1 2 3 4 0 -4 -3 -2 -1 -8 -1 -4 Унаиб.=0 Унаим.=-2 Найдите унаиб. и унаим. на отрезке функции у=-0,5х² -2 -6
Cлайд 18
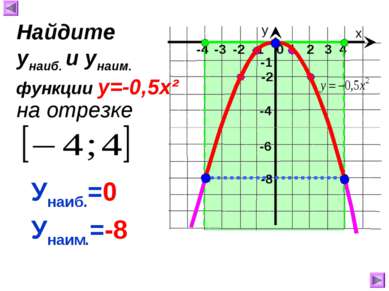х у 1 2 3 4 0 -4 -3 -2 -1 -8 -1 -4 Унаиб.=0 Унаим.=-8 Найдите унаиб. и унаим. на отрезке функции у=-0,5х² -2 -6
Cлайд 19
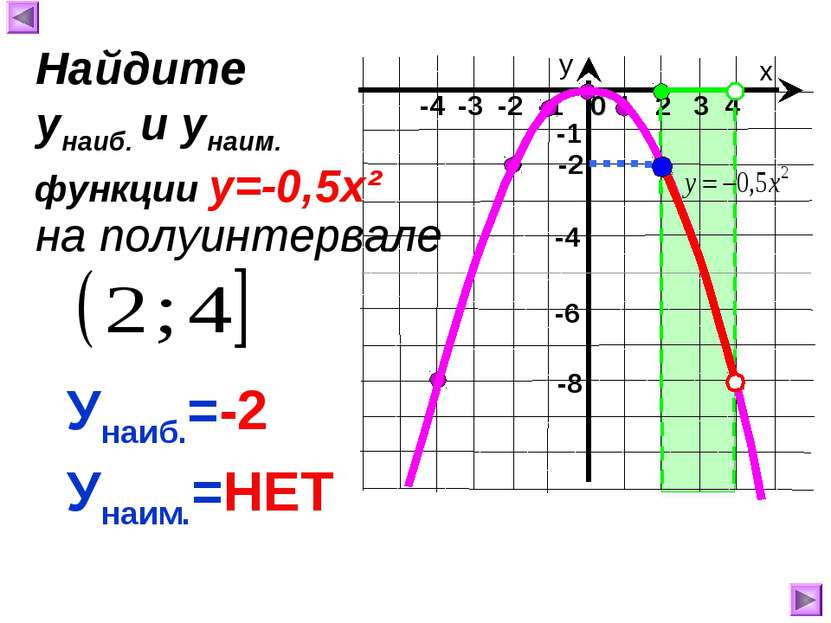
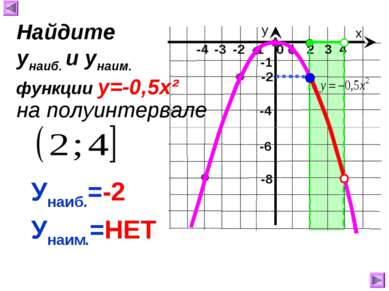х у 1 2 3 4 0 -4 -3 -2 -1 -8 -1 -4 Унаиб.=-2 Унаим.=НЕТ Найдите унаиб. и унаим. на полуинтервале функции у=-0,5х² -2 -6
Cлайд 20
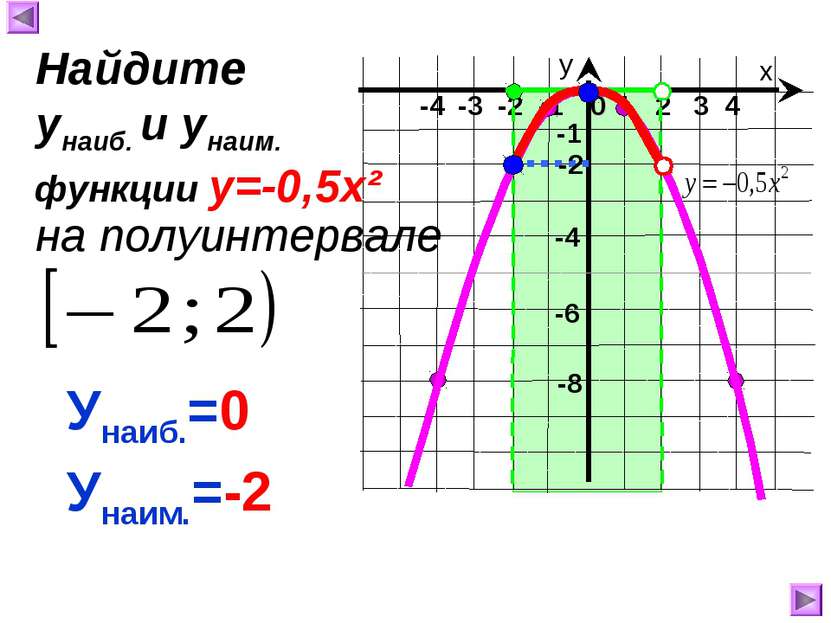
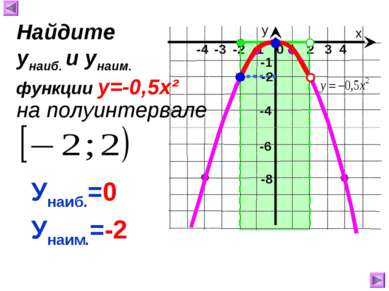х у 1 2 3 4 0 -4 -3 -2 -1 -8 -1 -4 Унаиб.=0 Унаим.=-2 Найдите унаиб. и унаим. на полуинтервале функции у=-0,5х² -2 -6
Cлайд 21
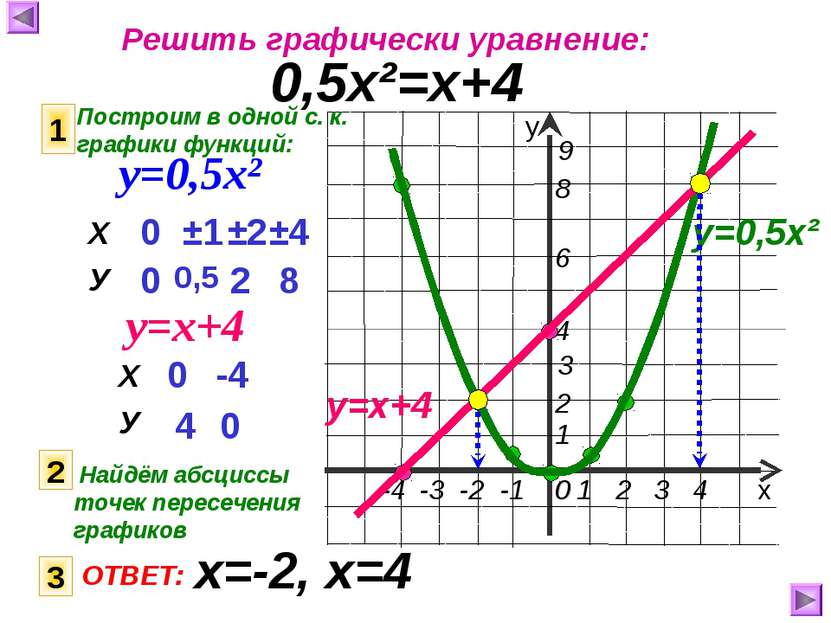
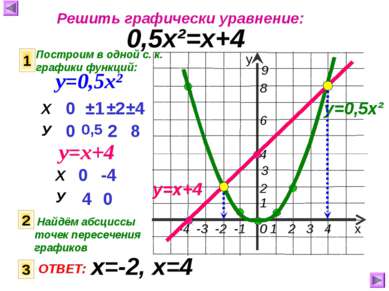Решить графически уравнение: 0,5х²=х+4 Построим в одной с. к. графики функций: 1 у=0,5х² у=х+4 0 0 ±1 0,5 ±2 ±4 2 8 0 4 -4 0 у=0,5х² у=х+4 2 Найдём абсциссы точек пересечения графиков 3 ОТВЕТ: х=-2, х=4 Х У Х У
Cлайд 22
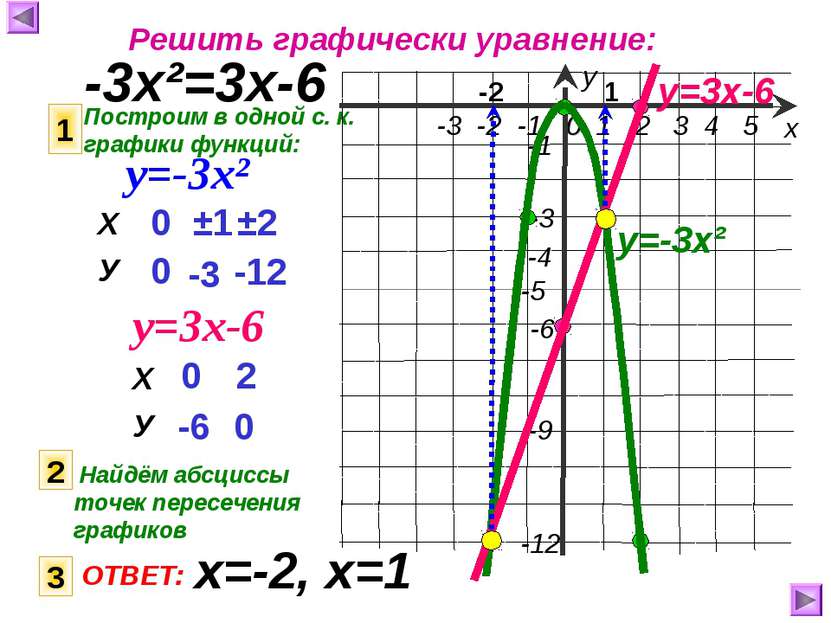
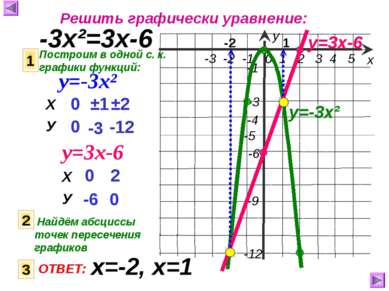Решить графически уравнение: -3х²=3х-6 Построим в одной с. к. графики функций: 1 у=-3х² у=3х-6 0 0 ±1 -3 ±2 -12 у=-3х² 0 -6 2 0 у=3х-6 2 Найдём абсциссы точек пересечения графиков 1 -2 3 ОТВЕТ: х=-2, х=1 Х У Х У
Cлайд 23
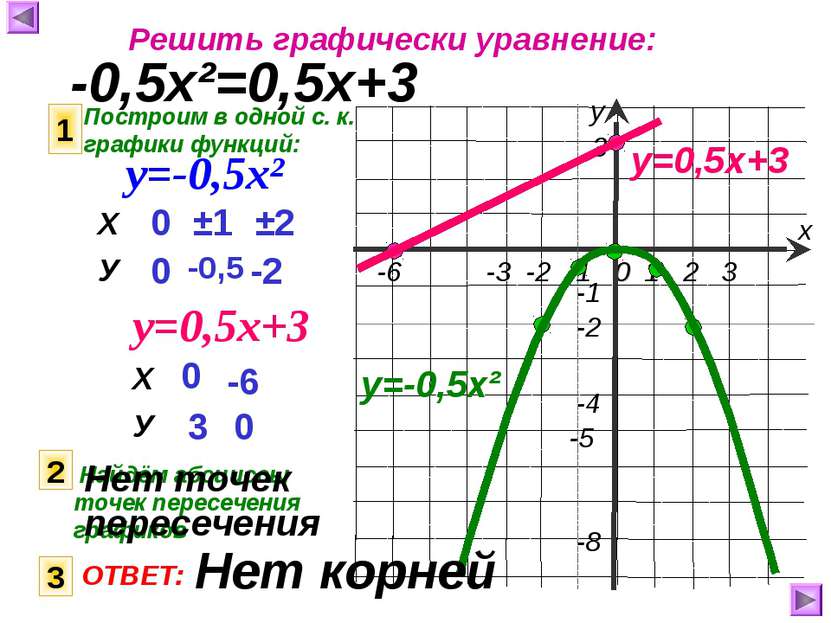
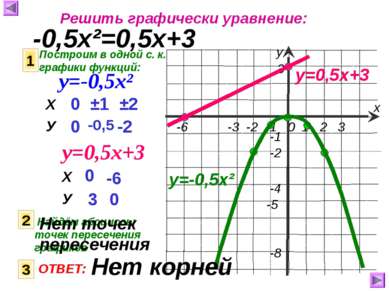Решить графически уравнение: -0,5х²=0,5х+3 Построим в одной с. к. графики функций: 1 у=-0,5х² у=0,5х+3 0 0 ±1 -0,5 ±2 -2 0 3 -6 0 у=0,5х+3 2 Найдём абсциссы точек пересечения графиков 3 ОТВЕТ: у=-0,5х² Нет точек пересечения Нет корней Х У Х У
Cлайд 24
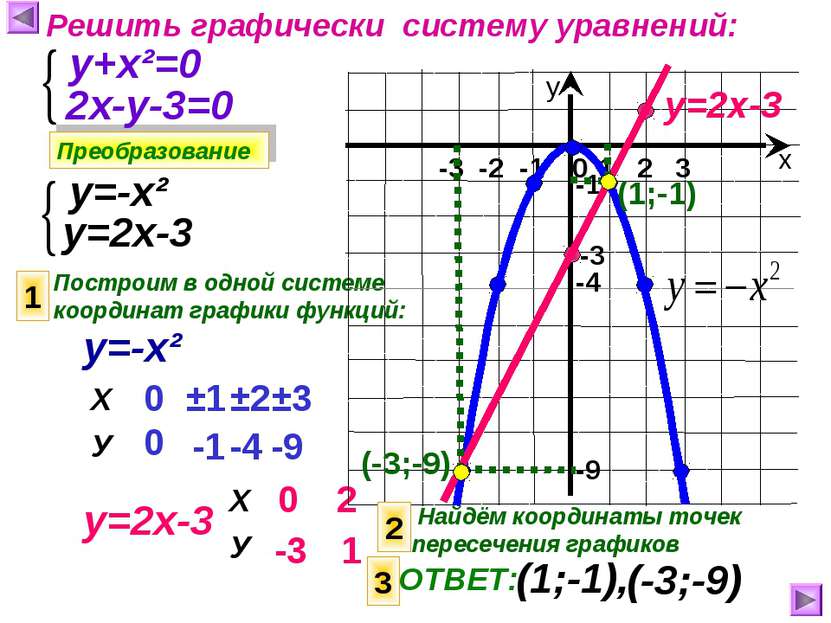
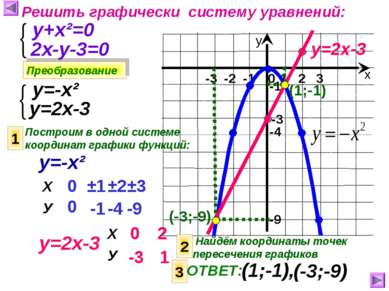Решить графически систему уравнений: Преобразование у+х²=0 2х-у-3=0 у=-х² у=2х-3 Построим в одной системе координат графики функций: 1 у=-х² у=2х-3 0 0 ±1 -1 ±2 ±3 -4 -9 0 -3 2 1 у=2х-3 -3 2 Найдём координаты точек пересечения графиков (1;-1) (-3;-9) 3 ОТВЕТ: (1;-1), (-3;-9) Х У Х У
Cлайд 25
Постройте график функции и опишите её свойства. f(x)= 2х²,если -1≤х≤1 2,если 1
Cлайд 26
f(x)= 2х²,если -1≤х≤1 х у 2,если 1
Cлайд 27
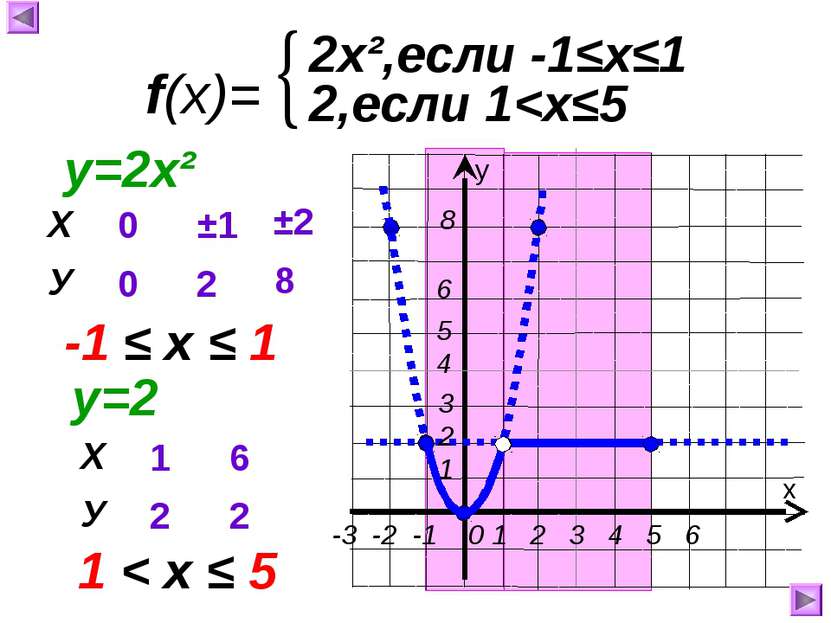
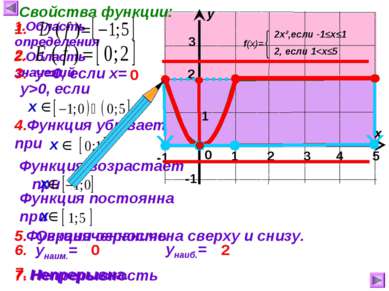1 2 3 4 5 Функция возрастает при Функция ограничена сверху и снизу. 1 х у 0 Свойства функции: 1.Область определения 3 -1 2 2.Область значений 3. у=0, если х= у>0, если 4.Функция убывает при 5. Ограниченность 1. 2. 5. 6. унаим.= унаиб.= 0 2 7. Непрерывность 7. Непрерывна. -1 0 Функция постоянна при
Cлайд 28
Постройте график функции Преобразование ГРАФИК Клики по прямоугольникам приводят к появлению преобразований и построений. 3
