X
Код презентации скопируйте его
Линейные уравнения
Скачать эту презентацию
Презентация на тему Линейные уравнения
Скачать эту презентациюCлайд 1
Линейные уравнения (Алгебра – 7 класс)
Cлайд 2
Электронный учебник Составила: учитель математики-информатики Терегулова И.В. МОУ «СОШ №1» 2008 год
Cлайд 3
Дорогой друг! Твоему вниманию представлен электронный учебник, где ты можешь найти необходимые сведенья для решения линейных уравнений. Освоив способы решения, ты можешь проверить свои знания, решив тестовые задания и самостоятельную работу, после чего компьютер поставит тебе оценку. Желаю удачи!
Cлайд 4
Равенство между двумя алгебраическими выражениями с одной переменной называют уравнением с одной неизвестной. Корнем уравнения называют значение переменной , при котором уравнение обращается в верное числовое равенство. Решить уравнение означает найти все его корни или доказать, что корней нет. Уравнения, которые имеют одни и те же корни, называются равносильными. Уравнения, которые не имеют корней, также считаются равносильными. Основные понятия:
Cлайд 5
Определение: уравнение вида а х = в (где х – переменная, а и в – некоторые числа) называется линейным уравнением с одной переменной. Отличительная особенность такого уравнения – переменная х входит в уравнение обязательно в первой степени.
Cлайд 6
Пример 1 Перечисленные уравнения являются линейными, так как имеют вид а х = в: а) 3 х=7 (где а=3, в=7); б) -2 х=5 (где а=?, в=?); в) 0х=-3 (где а=?, в=?); г)0х=0 (где а=?, в=?). Все линейные уравнения приводятся к виду а х = в с помощью тождественных преобразований.
Cлайд 7
Пример 2 В уравнении 2(3х-5)=х-3 переменная х входит в первой степени. Поэтому это уравнение является линейным. Приведём это уравнение к стандартному виду. В левой части раскроем скобки: 2 3х-2 5=х-3 или 6х-10=х-3. Перенесём слагаемые, содержащие х, в левую часть уравнения; числа – в правую. Приведём подобные слагаемые. Получаем: 6х-х=10-3 или 5х=7. Линейное уравнение имеет вид ах=в (где а=5, в=7)
Cлайд 8
При решении уравнений не забудь следующие свойства: если в уравнении перенести слагаемые из одной части в другую, изменив его знак, то получится уравнение, равносильное данному; Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение равносильное данному.
Cлайд 9
Пример 3 Перечисленные уравнения не являются линейными: 3х2+6х+7=0 (так как содержит переменную х во второй степени); 2х2-5х3= 3 (объясни сам) х(х-3)=х5 (объясни сам)
Cлайд 10
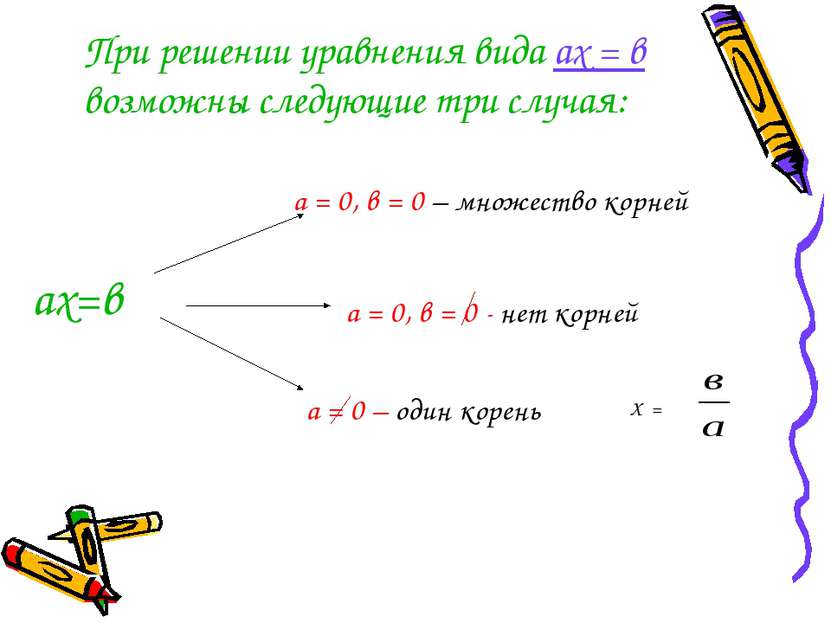
ах=в а = 0 – один корень а = 0, в = 0 - нет корней а = 0, в = 0 – множество корней При решении уравнения вида ах = в возможны следующие три случая: Х =
Cлайд 11
Пример 4 Решим уравнение 2 (3 х-1)=4 (х +3). Приведём это уравнение к стандартному виду. Раскроем скобки в обеих частях уравнения:2 3 х-2 1=4 х + 4 3 или 6 х - 2= 4 х + 12. Слагаемые, зависящие от х, перенесём в левую часть уравнения; числа – в правую, изменяя их знаки на противоположные: 6 х - 4х = 2+ 12. Приведём подобные слагаемые: 2х = 14 . В этом уравнении а=2 и в=14 . Уравнение имеет один корень х = =7
Cлайд 12
Пример 5 Решим уравнение 2( 3 х-1)=4 ( х+3)- 14 +2х. Приводим это уравнение к стандартному виду: 6 х -2= 4 х + 12 – 14 + 2 х или 6 х - 4 х - 2х=2 + 12-14, или 0х=0 (где а=0, в=0 ) . Очевидно, что при подстановке любого значения х получаем верное числовое равенство 0=0. Поэтому любое число является корнем этого уравнения (уравнение имеет бесконечно много корней).
Cлайд 13
Пример 6 Решим уравнение 2 (3 х-1)=4 ( х + 3)+2х Приводим это уравнение к стандартному виду: 6 х - 2= 4 х+ 12+ 2 х или 6 х - 4 х-2 х= 2+12 или 0х=14 (где а=0, в=14 ). Очевидно, что при подстановке любого значения х получаем неверное числовое равенство 0=14. Поэтому уравнение корней не имеет.
Cлайд 14
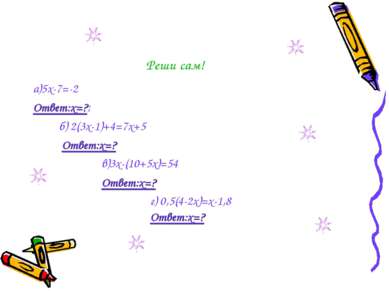Реши сам! а)5х-7=-2 Ответ:х=?; б) 2(3х-1)+4=7х+5 Ответ:х=? в)3х-(10+5х)=54 Ответ:х=? г) 0,5(4-2х)=х-1,8 Ответ:х=?
Cлайд 15
а)5x=-2+7 5x=5 х=1 Ответ:х=1 б) 6х-2+4=7х+5 6х-7х=5+2-4 -х=3 х=-3 Ответ:х=-3 в)3х-10-5х=54 -2х=54+10 -2х=64 х=64:(-2) х=-32 Ответ:х=-32 г) 2-х=х-1,8 -х-х=-1,8-2 -2х=-3,8 х=1,9 Ответ: х=1,9
Cлайд 16
Тестовая работа Проверь свои знания ответив на вопросы предложенные компьютером.
Cлайд 17
Самостоятельная работа Реши уравнения и компьютер оценит твою работу.
Cлайд 18
Не расстраивайся, если компьютер тебя не оценил. Вернись к слайду №4, попробуй начать всё сначала и у тебя обязательно всё получится!
Cлайд 19
Если ты прошёл тест, решил самостоятельную работу и учитель тебя похвалил, попробуй свои силы при решении следующих уравнений: 1. Реши уравнение: |3х + 8|=1 2. Найди значение параметра а, при котором уравнение (3а + 1) х = 2а+6 имеет корень х=2 Удачи тебе!
Cлайд 20
