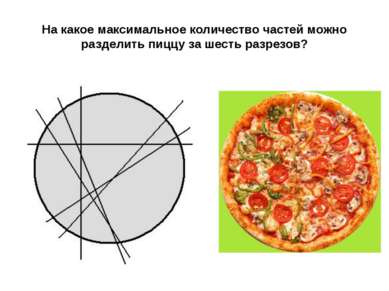
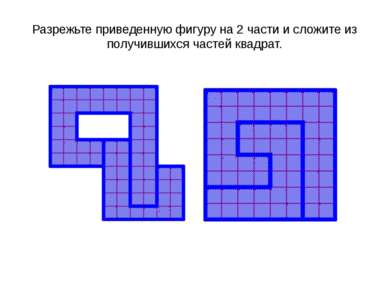
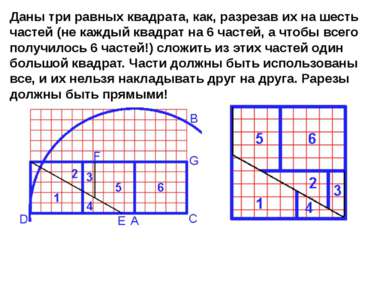
X
Код презентации скопируйте его
Задачи на разрезания и перекраивания фигур
Скачать эту презентацию
Презентация на тему Задачи на разрезания и перекраивания фигур
Скачать эту презентациюCлайд 1
Задачи на разрезания и перекраивания фигур Факультатив . Математика 5 класс Учитель математики школы №91 Г.А.Ларькина Г.Нижний Новгород
Cлайд 2
Разpежьте изобpаженную фигуpу по линиям клеток на 4 одинаковые части.
Cлайд 3
На какое максимальное количество частей можно разделить пиццу за шесть разрезов?
Cлайд 4
Разpежьте приведенную фигуpу на 2 части и сложите из получившихся частей квадpат.
Cлайд 5
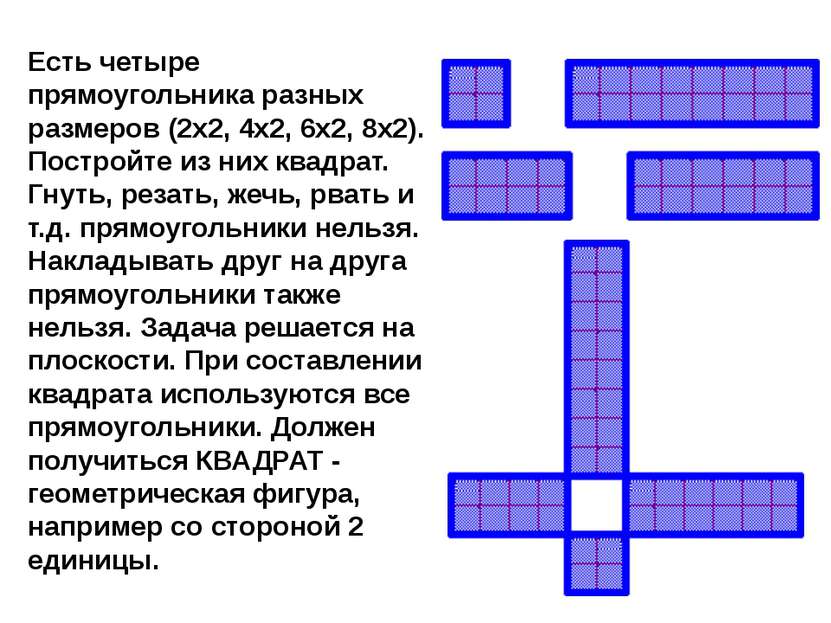
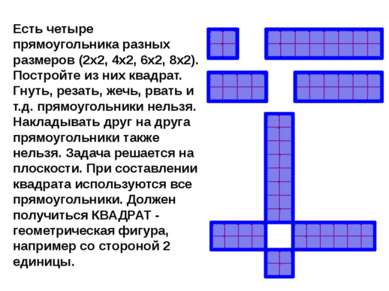Есть четыре прямоугольника разных размеров (2x2, 4x2, 6x2, 8x2). Постройте из них квадрат. Гнуть, резать, жечь, рвать и т.д. прямоугольники нельзя. Hакладывать друг на друга прямоугольники также нельзя. Задача решается на плоскости. При составлении квадрата используются все прямоугольники. Должен получиться КВАДРАТ - геометрическая фигура, например со стороной 2 единицы.
Cлайд 6
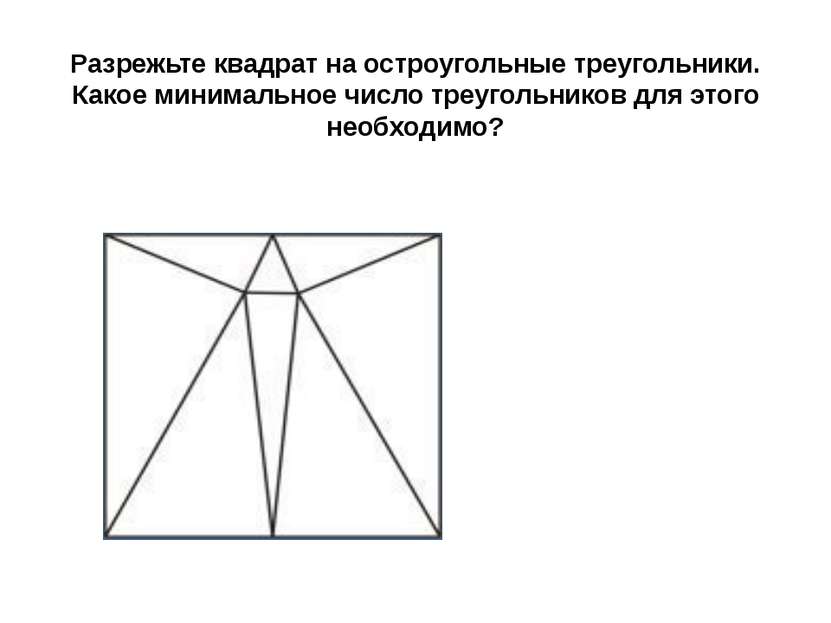
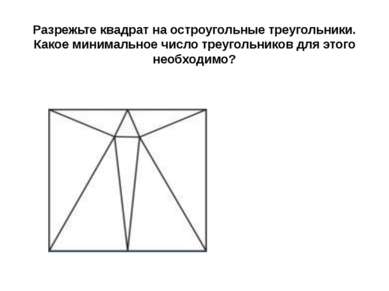Разрежьте квадрат на остроугольные треугольники. Какое минимальное число треугольников для этого необходимо?
Cлайд 7
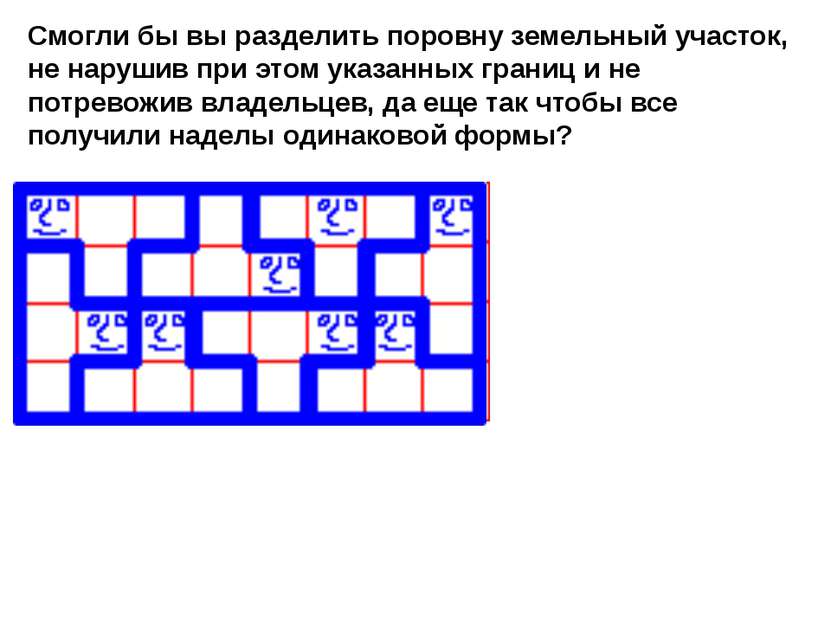
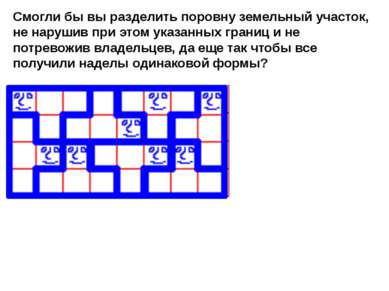Смогли бы вы разделить поровну земельный участок, не нарушив при этом указанных границ и не потревожив владельцев, да еще так чтобы все получили наделы одинаковой формы?
Cлайд 8
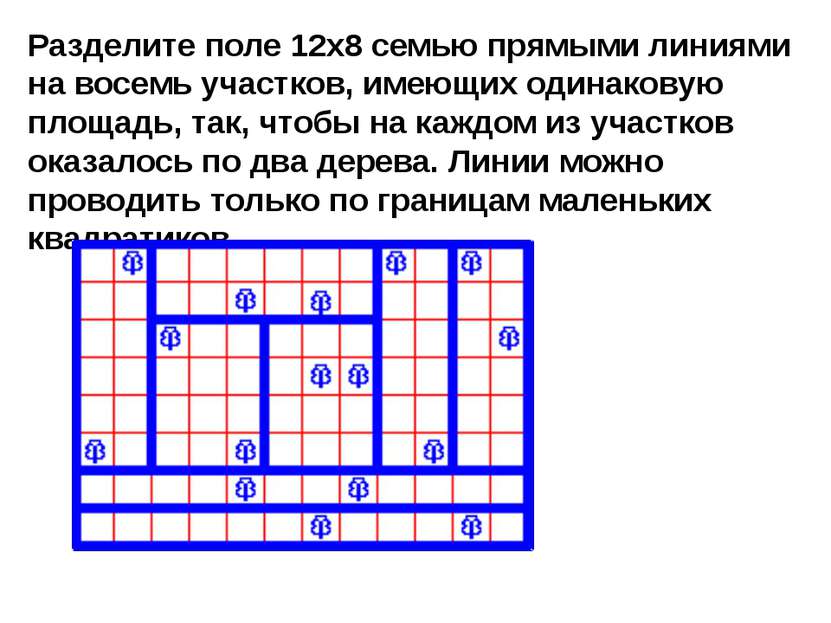
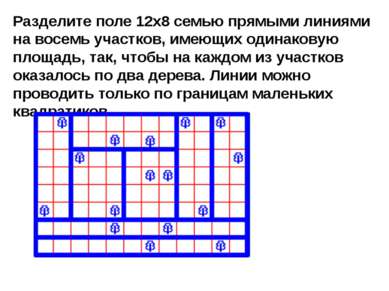Разделите поле 12x8 семью прямыми линиями на восемь участков, имеющих одинаковую площадь, так, чтобы на каждом из участков оказалось по два дерева. Линии можно проводить только по границам маленьких квадратиков.
Cлайд 9
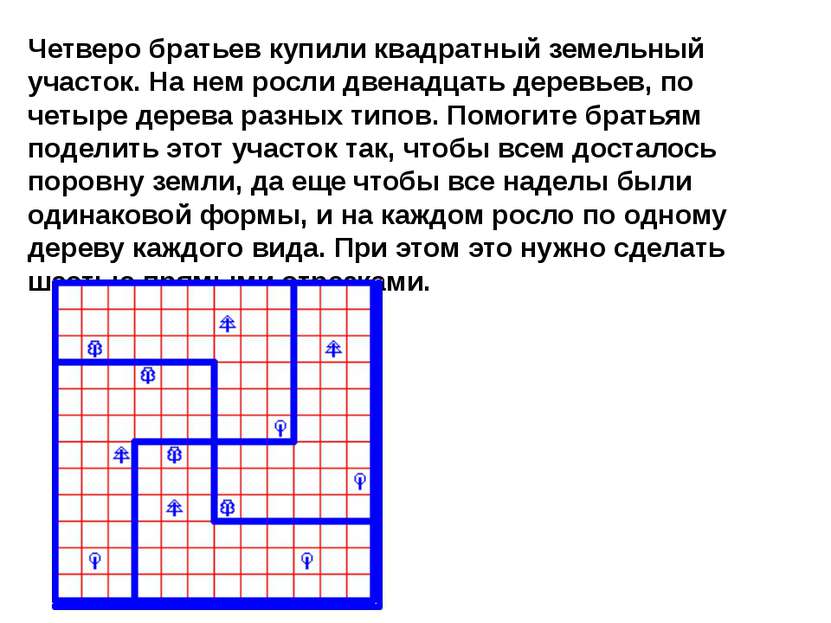
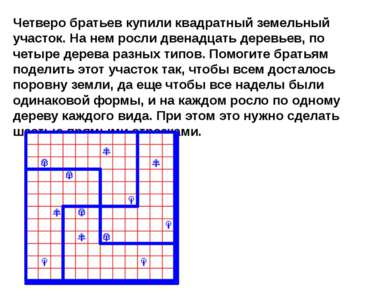Четверо братьев купили квадратный земельный участок. На нем росли двенадцать деревьев, по четыре дерева разных типов. Помогите братьям поделить этот участок так, чтобы всем досталось поровну земли, да еще чтобы все наделы были одинаковой формы, и на каждом росло по одному дереву каждого вида. При этом это нужно сделать шестью прямыми отрезками.
Cлайд 10
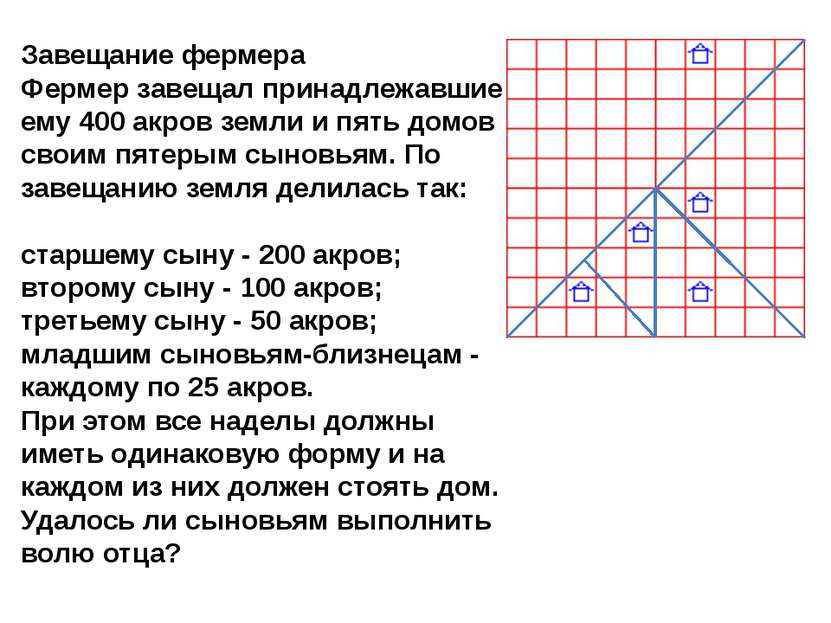
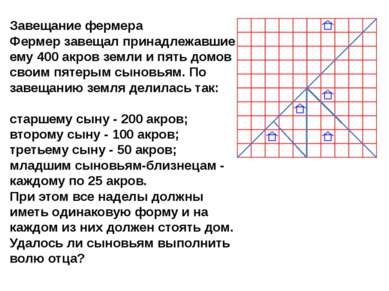Завещание фермера Фермер завещал принадлежавшие ему 400 акров земли и пять домов своим пятерым сыновьям. По завещанию земля делилась так: старшему сыну - 200 акров; второму сыну - 100 акров; третьему сыну - 50 акров; младшим сыновьям-близнецам - каждому по 25 акров. При этом все наделы должны иметь одинаковую форму и на каждом из них должен стоять дом. Удалось ли сыновьям выполнить волю отца?
Cлайд 11
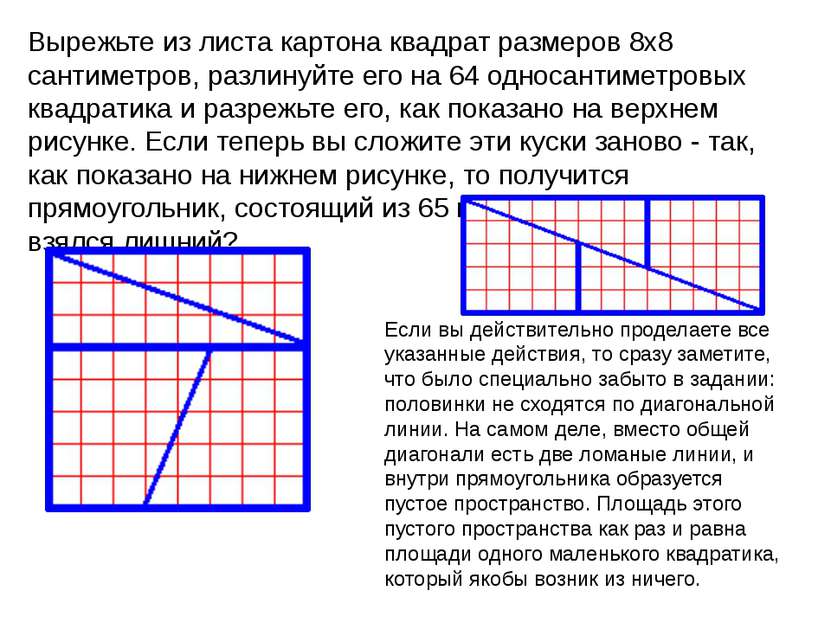
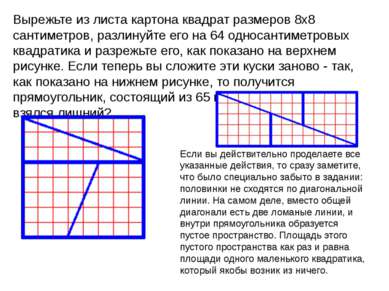Вырежьте из листа картона квадрат размеров 8х8 сантиметров, разлинуйте его на 64 односантиметровых квадратика и разрежьте его, как показано на верхнем рисунке. Если теперь вы сложите эти куски заново - так, как показано на нижнем рисунке, то получится прямоугольник, состоящий из 65 квадратиков. Откуда же взялся лишний? Если вы действительно проделаете все указанные действия, то сразу заметите, что было специально забыто в задании: половинки не сходятся по диагональной линии. На самом деле, вместо общей диагонали есть две ломаные линии, и внутри прямоугольника образуется пустое пространство. Площадь этого пустого пространства как раз и равна площади одного маленького квадратика, который якобы возник из ничего.
Cлайд 12
Даны три равных квадрата, как, разрезав их на шесть частей (не каждый квадрат на 6 частей, а чтобы всего получилось 6 частей!) сложить из этих частей один большой квадрат. Части должны быть использованы все, и их нельзя накладывать друг на друга. Рарезы должны быть прямыми!
