X
Код презентации скопируйте его
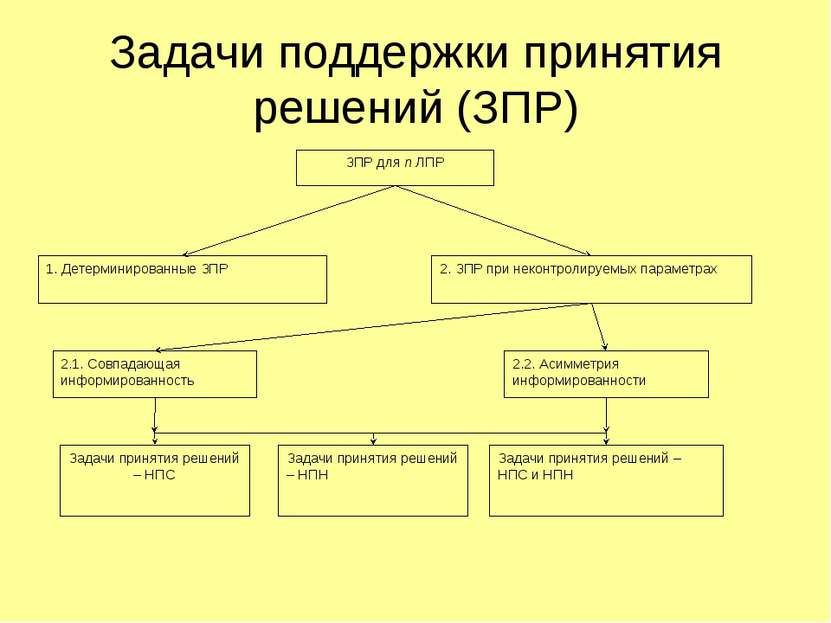
Задачи поддержки принятия решений (ЗПР)
Скачать эту презентацию
Презентация на тему Задачи поддержки принятия решений (ЗПР)
Скачать эту презентациюCлайд 1
Задачи поддержки принятия решений (ЗПР)
Cлайд 2
Теоретико-игровые модели
Cлайд 3
* Задачи поддержки принятия решений ЗПР в условиях определенности (1) ЗПР при неконтролируемых параметрах (2)
Cлайд 4
* Задачи поддержки принятия решений Принцип осреднения параметров (3) Принцип гарантированного результата (4) Определение 1. Пусть , тогда вариационным расширением (ВР) задачи (2) будем называть следующую задачу (5)
Cлайд 5
* Пример Игра «Государство-Предприниматели» Целевая функция центра: Целевая функция предпринимателей: x – предпринимательская прибыль (0≤ x ≤ xmax); k – доля прибыли, отчисляемая в качестве налогов (0≤ k ≤ 1); φ(x,δ) – предпринимательские риски.
Cлайд 6
* Вариационное расширение: Пример
Cлайд 7
* Пример игры 2-х лиц с совпадающими интересами при асимметрии информированности Целевая функция (6) при условиях (7)
Cлайд 8
* Игры n лиц Определение 2. Ситуация является равновесной по Нэшу, если для всех справедливо неравенство: Предположим Тогда задача (6), (7) примет вид:
Cлайд 9
* Задачи поддержки принятия решений при асимметрии информированности w=(w1,w2,…,wm) – случайный вектор с функцией распределения Φ(w) множество Im={1,2,…,m} – индексы компонент вектора w множество Si Im – совокупность индексов, определяющих информационную структуру i- ой решающей функции, i In={1,2,…,n} x=(x1,x2,…,xn) – вектор управления, где xi=xi(di), di=(wj), j Si. Таким образом, задача примет вид: Ji (x)=M[Fi (x(w),w)]→max, i In (8) xi Xi условие разной информированности приводит к отсутствию соответствующей переменной :
Cлайд 10
* Вариационное расширение Целевая функция центра: Целевая функция предпринимателей: Цели игроков Максимизировать целевую функцию путем изменения ставки налога Максимизировать целевую функцию путем изменения совокупной активности Информационные гипотезы Центр знает вероятностное распределение параметра δ, а предприниматели – его точное значение. Компромисс центра и предпринимателей достигается в ситуациях равновесия по Штакельбергу. Решение при
Cлайд 11
* Задачи поддержки принятия решений при асимметрии информированности Игра в нормальной форме: (9)
Cлайд 12
* Необходимые условия оптимальности Функция Лагранжа: Уравнение Эйлера: Условие трансверсальности: (10)
Cлайд 13
* Игра двух лиц при асимметрии информированности (11) (12)
Cлайд 14
* Игра двух лиц при асимметрии информированности Утверждение 1 Пусть компоненты случайного вектора w есть независимые случайные величины, тогда равновесие по Нэшу задачи (12) при условиях (11), и a11, b22 0 достигается на линейных по своим переменным функциях и , где a11 и b22 элементы матриц A и B соответственно.
Cлайд 15
* Игра двух лиц при асимметрии информированности (13)
Cлайд 16
* Игра двух лиц при асимметрии информированности Утверждение 2 Решение задачи (12) при условиях (11), в концепции равновесия Нэша существует и единственно, если выполняются условия:
Cлайд 17
Задача стимулирования в активных системах Обозначим – действие i-го АЭ, – множество активных элементов. z = Q(y), где z –результат деятельности АЭ, входящих в систему. Пусть индивидуальные затраты i-го АЭ будут Функцию стимулирования для i-го АЭ обозначим тогда, целевая функция i-го АЭ примет вид: Целевая функция центра будет выражаться как разность между результатом деятельности системы и суммарными затратами на стимулирование:
Cлайд 18
Задача стимулирования в активных системах Ограничения . а) функция непрерывна по всем переменным; б) , не убывает по ; в) ; г) ; Функции стимулирования кусочно-непрерывные и принимают неотрицательные значения. Целевая функция центра непрерывна по всем переменным и достигает максимума при не нулевых действиях агентов.
Cлайд 19
Задача стимулирования в активных системах с разной информированностью АЭ Обозначим – действие i-го АЭ, – множество АЭ z = Q(u), где z –результат деятельности АЭ, входящих в систему. Пусть индивидуальные затраты i-го АЭ будут Для оценки затрат будем использовать усредненное значение: где – математическое ожидание. Функцию стимулирования для i-го АЭ обозначим тогда, целевая функция i-го АЭ примет вид: Целевая функция центра будет выражаться как разность между результатом деятельности системы и суммарными затратами на стимулирование:
Cлайд 20
Задача стимулирования в активных системах с разной информированностью АЭ Ограничения . ,где а) функция , является неубывающей по , если и выполнено неравенство ; б) затраты i-го АЭ не убывают по ; в) ; г) ; Функционалы стимулирования кусочно-непрерывные и принимают неотрицательные значения. Целевая функция центра непрерывна по всем переменным и достигает максимума при не нулевых действиях агентов.
Cлайд 21
Пусть ситуация равновесия в игре , тогда является ситуацией равновесия для игры
Cлайд 22
Задача стимулирования в случае квадратичной структуры Выпишем функции Лагранжа , : где – множители Лагранжа. Уравнение Эйлера: Условие трансверсальности: Отсюда система уравнений Эйлера путем несложных преобразований сводится к интегральному уравнению Фредгольма: где , , , ,
Cлайд 23
Пример задачи стимулирования второго рода Рассмотрим задачу стимулирования второго рода в АС с двумя АЭ, имеющими функции затрат: где – некоторый параметр, – оценка квалификации АЭ. Пусть функция дохода центра Фонд заработной платы ограничен величиной R (глобальное ограничение) Центр использует систему стимулирования: Задача центра сводится к поиску оптимальных реализуемых действий:
Cлайд 24
Пример задачи стимулирования второго рода Задачу (6) решим с помощью метода множителей Лагранжа. Выпишем функцию Лагранжа: где – множитель Лагранжа, . Необходимые условия: , решения не существует , решение существует и имеет вид: и ,решение будет следующим:
Cлайд 25
Пример задачи стимулирования второго рода Матрица вторых производных: Выпишем главные миноры матрицы : В обоих точках достигается максимум функции, найдем значения данной функции в точках (10) и (11) и сравним их: Абсолютный максимум достигается в первой точке.
Cлайд 26
Пример задачи стимулирования второго рода при разной информированности активных элементов Рассмотрим задачу стимулирования второго рода в АС с двумя АЭ, имеющими функции затрат: , где – некоторый параметр, – оценка квалификации АЭ, Пусть функция дохода центра Фонд заработной платы ограничен величиной R (глобальное ограничение) Центр использует систему стимулирования: Задача центра сводится к поиску оптимальных реализуемых действий: Разная информированность АЭ:
Cлайд 27
Пример задачи стимулирования второго рода при разной информированности активных элементов Для решения задачи воспользуемся методом множителей Лагранжа: где – множитель Лагранжа, . Необходимые условия: Обозначим: Отсюда система () путем несложных преобразований сводится к интегральному уравнению: где , , ,
Cлайд 28
Пример задачи стимулирования второго рода при разной информированности активных элементов Применим метод моментов для решения интегрального уравнения Фредгольма: Пусть в качестве линейно независимой системы возьмем следующую: Возьмем , , и отрезок . Рассмотрим систему (i=1,2,3), где , , . Откуда решение уравнения () имеет вид:
