X
Код презентации скопируйте его
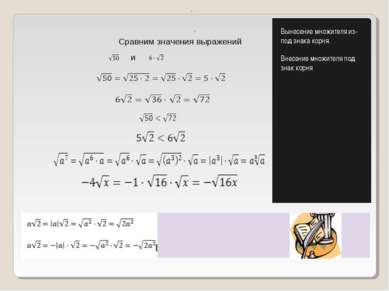
Преобразование выражений содержащих квадратные корни
Скачать эту презентацию
Презентация на тему Преобразование выражений содержащих квадратные корни
Скачать эту презентациюCлайд 1
Преобразование выражений, содержащих квадратные корни. Презентацию подготовила учитель математики Пухальская Надежда Александровна МБОУ СОШ №14 им. А.Ф.Лебедева г. Томска Урок алгебры в 8 классе
Cлайд 2
Свойства арифметического квадратного корня Квадратный корень из произведения и дроби Квадратный корень из степени При любом
Cлайд 3
Теорема 1 Корень из произведения неотрицательных множителей равен произведению корней из этих множителей
Cлайд 4
Теорема 2 Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя. Рассмотрим примеры:
Cлайд 5
Квадратный корень из степени Чтобы извлечь корень из степени с чётным показателем , надо представить подкоренное выражение в виде квадрата некоторого выражения и воспользоваться тождеством: При любом значении x равенство верное
Cлайд 6
, если a>0 , если a
Cлайд 7
Рассмотрим решение примеров №818(ж, з, и, к)
Cлайд 8
Рассмотрим решение примеров №420 (а, б, в, г, д) №420 е) №419(а, б)
Cлайд 9
В 1626 году нидерландский математик А.Ширар ввел близкое к современному обозначение корня V. Если над этим знаком стояла цифра 2, то это означало корень квадратный, если 3 – кубический. Это обозначение стало вытеснять знак Rx. Однако долгое время писали Vа+в с горизонтальной чертой над суммой. Лишь в 1637 году Рене Декарт соединил знак корня с горизонтальной чертой, применив в своей «Геометрии» современный знак корня . Этот знак вошёл во всеобщее употребление лишь в начале XVIII века. Из истории преобразования выражений, содержащих квадратные корни.
Cлайд 10
Подведём Итоги ! Копия 42_hyR.xls
Cлайд 11
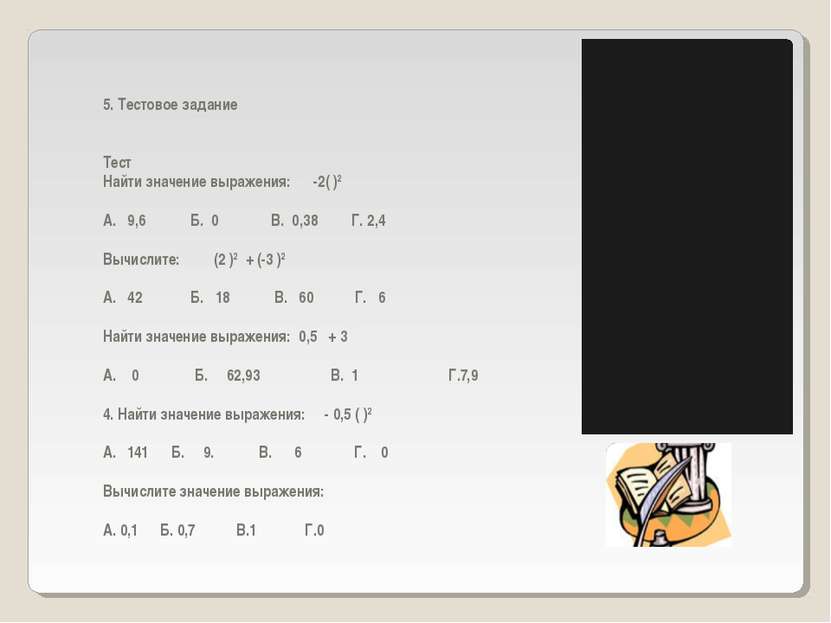
5. Тестовое задание Тест Найти значение выражения: -2( )2 А. 9,6 Б. 0 В. 0,38 Г. 2,4 Вычислите: (2 )2 + (-3 )2 А. 42 Б. 18 В. 60 Г. 6 Найти значение выражения: 0,5 + 3 А. 0 Б. 62,93 В. 1 Г.7,9 4. Найти значение выражения: - 0,5 ( )2 А. 141 Б. 9. В. 6 Г. 0 Вычислите значение выражения: А. 0,1 Б. 0,7 В.1 Г.0
Cлайд 12
Используемая литература и интернет-ресурсы презентации к уроку: http://yandex.ru/yandsearch?p http://ru.wikipedia.org/wiki/ Учебник – «Алгебра 8, автор – Макарычев Ю.Н. и др. под редакцией Теляковского. Издательство «Просвещение».
