X
Код презентации скопируйте его
Математическая логика
Скачать эту презентацию
Презентация на тему Математическая логика
Скачать эту презентациюCлайд 1
Предисловие В повседневной жизни мы часто сталкиваемся с ситуациями, когда не знаем, как прийти к выводу из предпосылок и получить истинное знание о предмете размышления. Логика служит одним из инструментов почти любой науки. Пример тому школьный курс математики.
Cлайд 2
Использованная литература Шабунин М.И. Математика. Алгебра. Начала анализа. http://ru.wikipedia.org
Cлайд 3
Предмет логики Логика (др.-греч. «λογική» — «искусство рассуждения») — наука, изучающая законы и формы мышления.
Cлайд 4
Высказывания Высказывание – утвердительное предложение, относительно которого можно сказать истинно оно или ложно. Обычно высказывания обозначаются заглавными латинскими буквами, а само предложение заключается в фигурные скобки. Понятие высказывания является исходным понятием математической логики.
Cлайд 5
Работу выполнили Ученицы 11 А класса: Баженова Наталья Луценко Ксения Масленникова Людмила Саяпина Юлия Под руководством учителя математики Мигунова Фёдора Юрьевича
Cлайд 6
Для предикатов характерны те же действия, что и для высказываний, а именно: Конъюнкция Дизъюнкция Импликация Эквиваленция и др. ПРЕДИКАТЫ
Cлайд 7
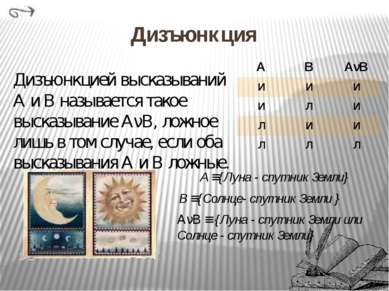
Алгебра высказываний Дизъюнкция Импликация Эквиваленция Строгая дизъюнкция Конъюнкция Действия над высказываниями Отрицание
Cлайд 8
Тогда, слушайте загадку! Да, капитан! Так точно, капитан! Я не слышу!! Согласно инструкции я должен находиться на судне всегда, за исключением случаев, когда с судна выгружают груз, если же груз не выгружают, то рулевой никогда не отсутствует, если не отсутствую и я. В каких случаях рулевой обязан присутствовать на судне? Вы готовы дети?
Cлайд 9
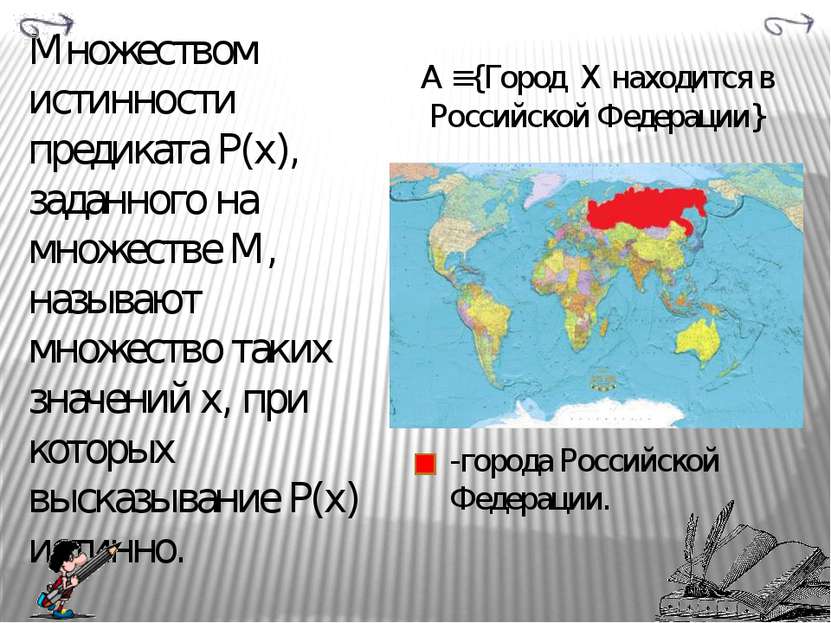
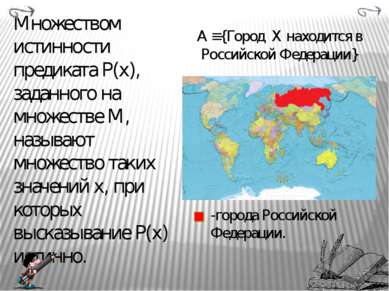
Предикаты Утверждение, зависящее от переменной, заданной на определенном множестве и обращающееся в верное высказывание при конкретном значении переменной, называется неопределенным высказыванием или предикатом. A(х) ≡ {d=x+34} d
Cлайд 10
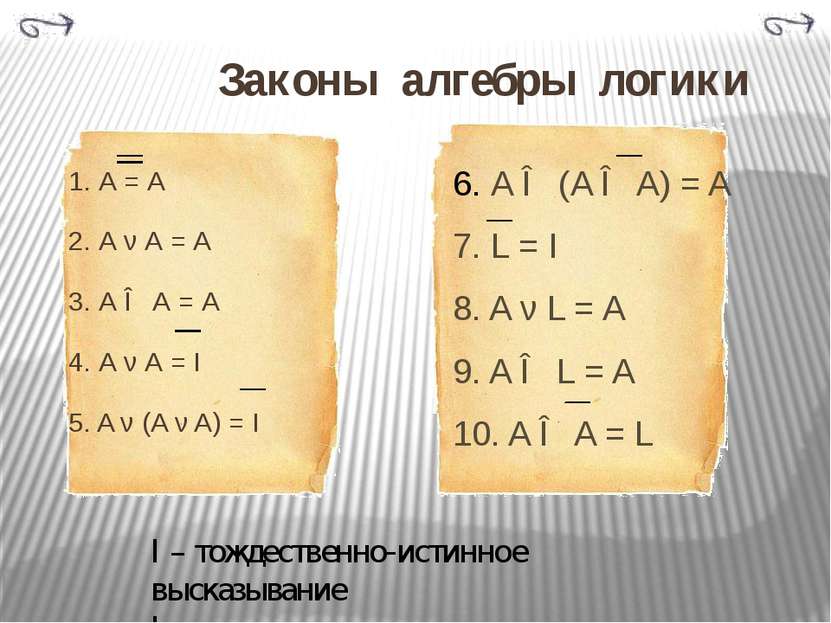
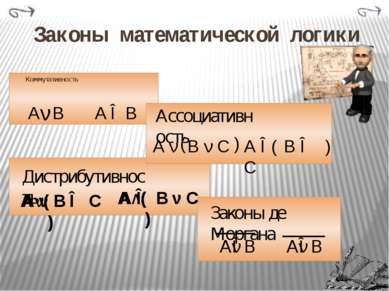Законы алгебры логики 1. А = А 2. А ν А = А 3. А ∧ А = А 4. А ν А = I 5. A ν (A ν A) = I 6. A ∧ (A ∧ A) = A 7. L = I 8. A ν L = A 9. A ∧ L = A 10. A ∧ A = L I – тождественно-истинное высказывание L – тождественно-ложное высказывание
Cлайд 11
Отрицание Отрицанием высказывания А называется такое высказывание, что В ложно, когда А истинно и В истинно, когда А ложно. А А И Л Л И
Cлайд 12
Правила пользования презентацией Выход в содержание Возврат к предыдущему слайду Переход к следующему слайду Подчёркнутое слово Гиперссылка
Cлайд 13
Cлайд 14
Cлайд 15
Cлайд 16
Cлайд 17
Cлайд 18
Cлайд 19
Cлайд 20
Cлайд 21
Cлайд 22
Cлайд 23
Cлайд 24
Cлайд 25
Cлайд 26
Cлайд 27
Cлайд 28
