X
Код презентации скопируйте его
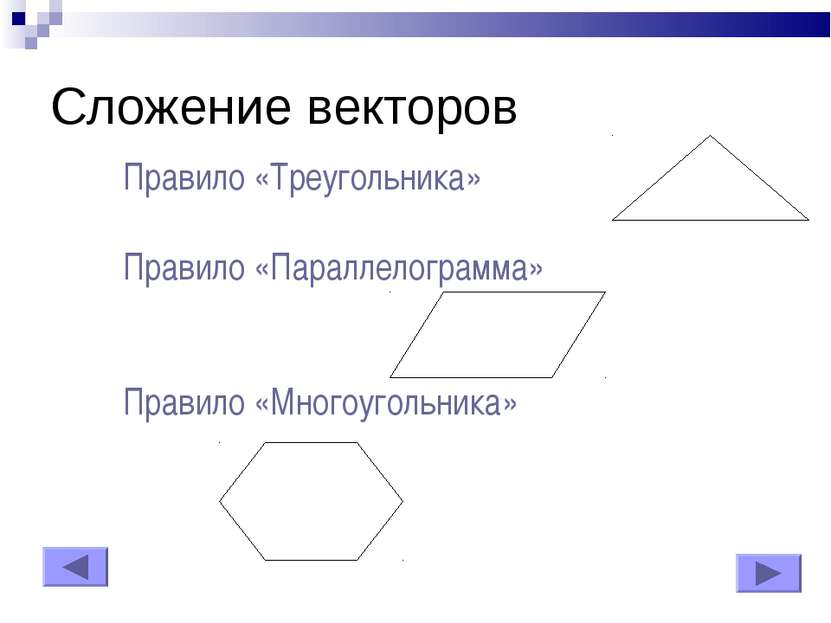
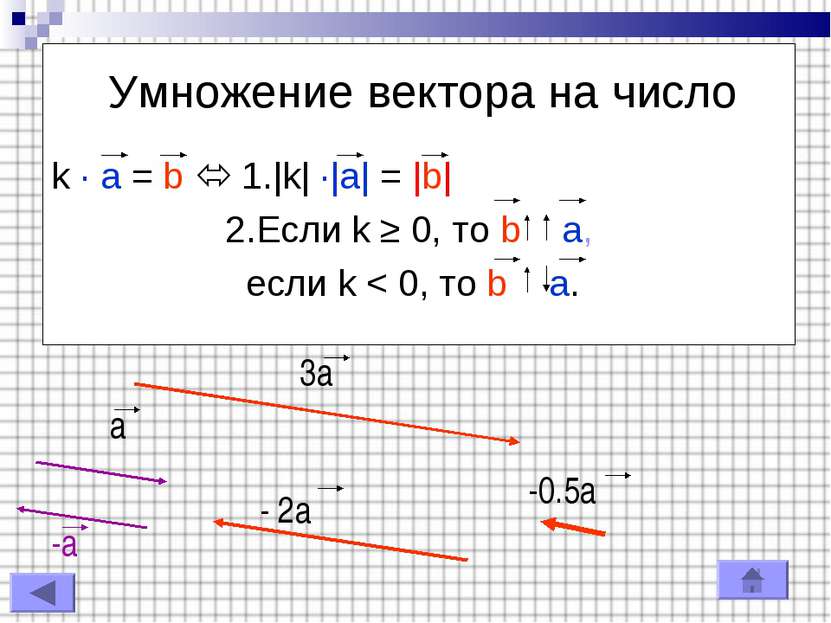
Действия с векторами
Скачать эту презентацию
Презентация на тему Действия с векторами
Скачать эту презентациюCлайд 1
Действия с векторами © Кузнецова О.И., учитель математики ГОУ СОШ №324 2007 год
Cлайд 2
Оглавление Сложение векторов. Вычитание векторов. Умножение вектора на число.
Cлайд 3
Сложение векторов Правило «Треугольника» Правило «Параллелограмма» Правило «Многоугольника»
Cлайд 4
Правило «Треугольника» a + b = AB + BC = AC (для неколлинеарных векторов) b a A B C A C
Cлайд 5
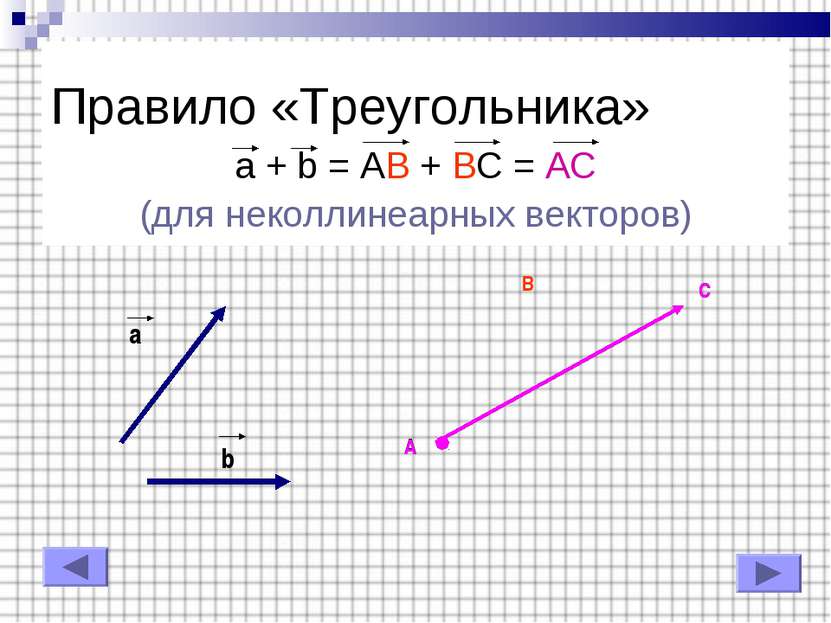
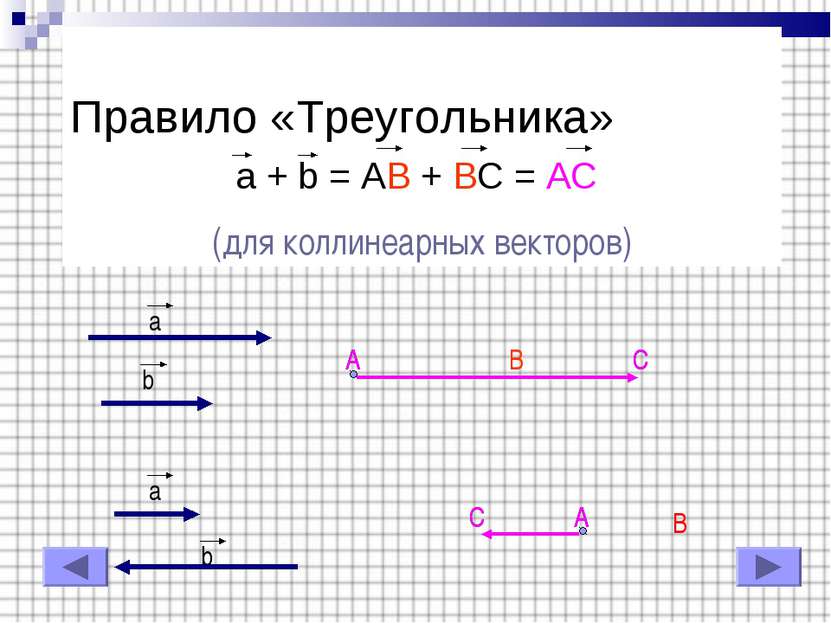
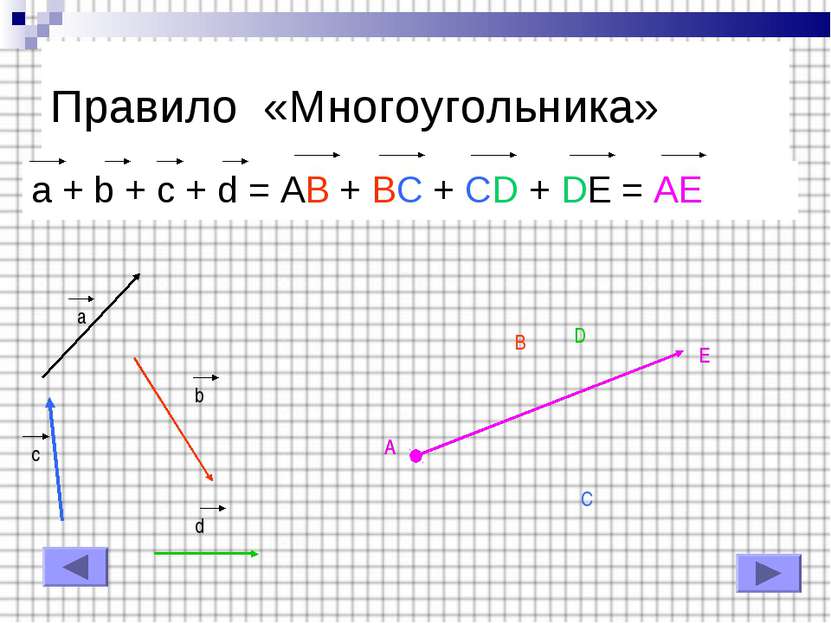
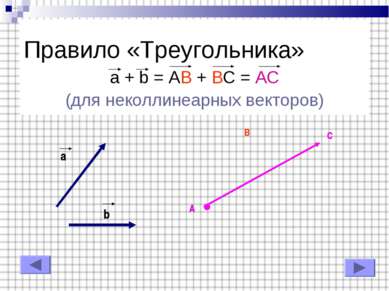
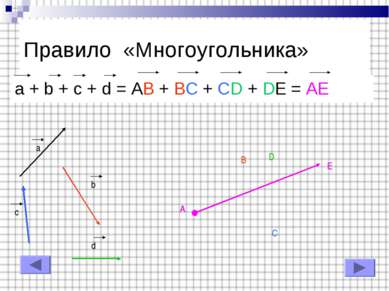
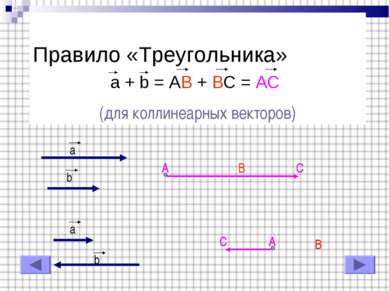Правило «Треугольника» a + b = AB + BC = AC (для коллинеарных векторов) a b a b A B C C A B A C A C
Cлайд 6
Правило «Параллелограмма» a + b = OA + OB = OC b a O A B C C
Cлайд 7
Правило «Многоугольника» a + b + c + d = AB + BC + CD + DE = AE a b c d A B C D E E A
Cлайд 8
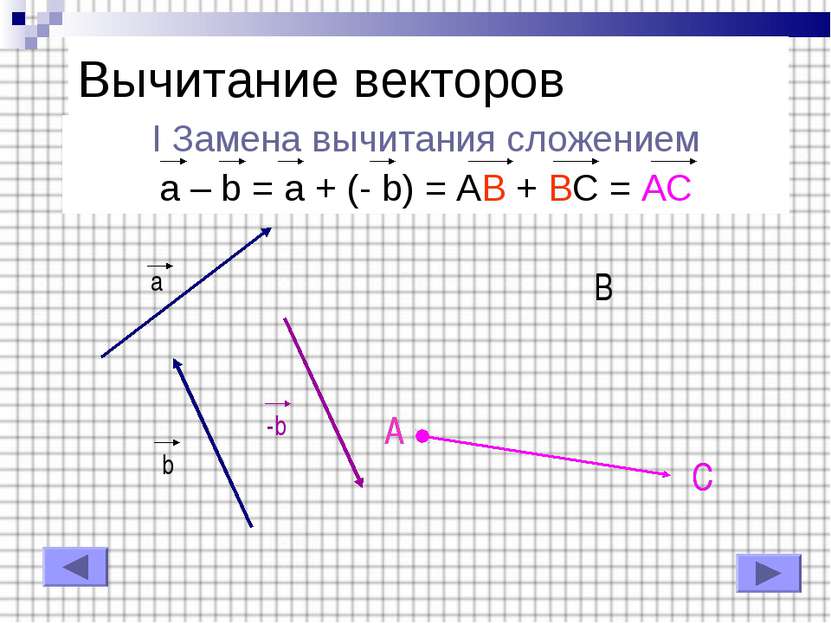
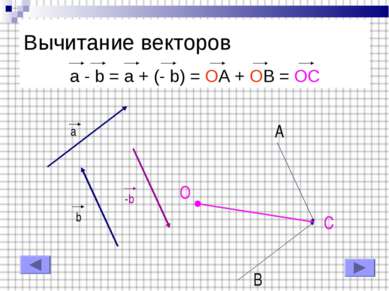
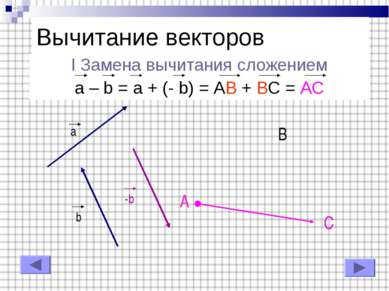I Замена вычитания сложением a – b = a + (- b) = AB + BC = AC Вычитание векторов a b -b A B C A C
Cлайд 9
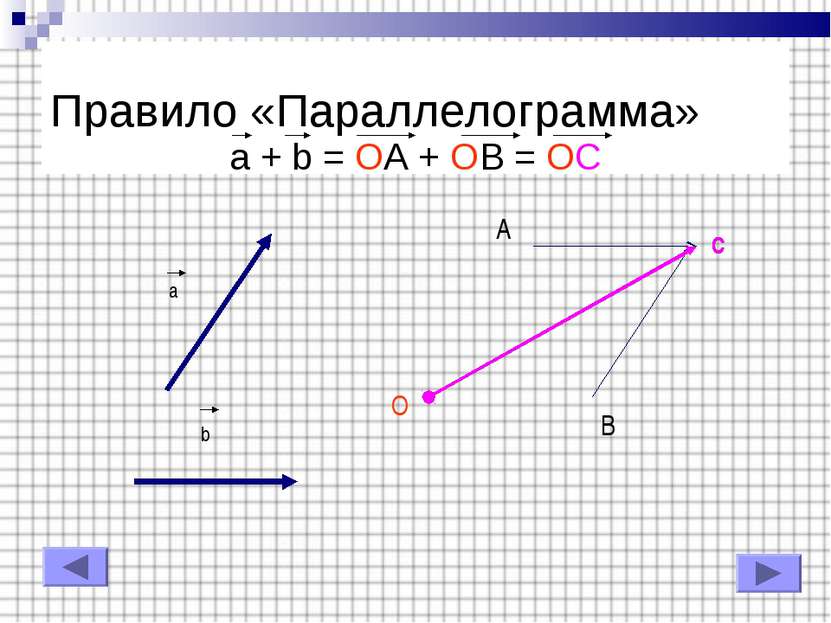
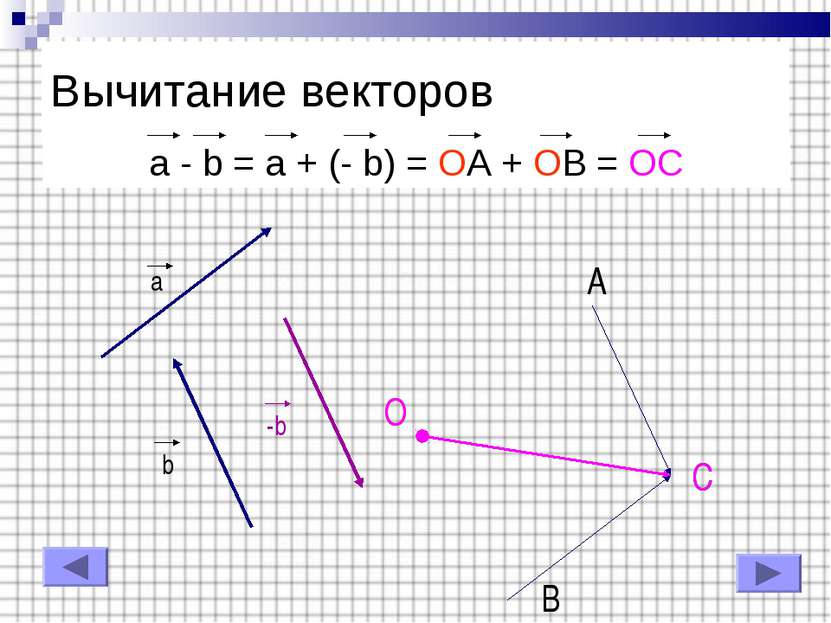
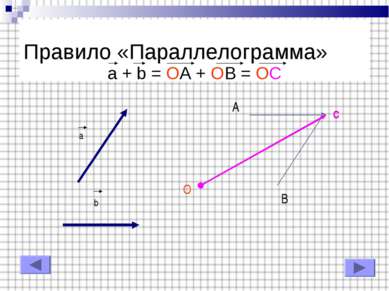
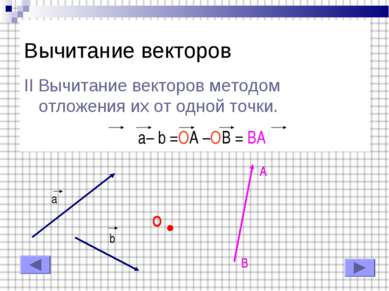
Вычитание векторов Какое правило сложения было использовано в предыдущем слайде ? Ответ: Правило «Треугольника». Попробуйте выполнить вычитание, используя сложение по правилу «Параллелограмма»
Cлайд 10
Вычитание векторов a - b = a + (- b) = OA + OB = OC a b -b A B C O C O
Cлайд 11
Вычитание векторов II Вычитание векторов методом отложения их от одной точки. a– b =OA –OB = BA a b O A B B A
Cлайд 12
Умножение вектора на число k · a = b 1.|k| ·|a| = |b| 2.Если k ≥ 0, то b a, если k < 0, то b a. a 3a
