X
Код презентации скопируйте его
Квадратичная функция, её свойства и график
Скачать эту презентациюПрезентация на тему Квадратичная функция, её свойства и график
Скачать эту презентациюCлайд 2
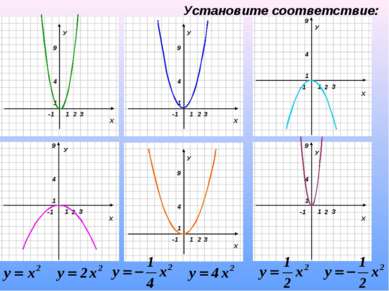
 Цели: ввести понятие квадратичной функции; научится строить график функции у=ах2 + ах +с и описывать свойства данной функции по графику; установить закономерность между графиком функции у=ах2 и значением коэффициента а.
Цели: ввести понятие квадратичной функции; научится строить график функции у=ах2 + ах +с и описывать свойства данной функции по графику; установить закономерность между графиком функции у=ах2 и значением коэффициента а.
Cлайд 3
 Два жучка бежали в домик. Им навстречу муравей. Сколько будет насекомых? Сосчитай - ка их скорей!
Два жучка бежали в домик. Им навстречу муравей. Сколько будет насекомых? Сосчитай - ка их скорей!
Cлайд 4
 Определение. Квадратичной функцией называется функция, которую можно задать формулой вида у=ах2+bx+c, где х – независимая переменная, а, b и с – некоторые числа, причем а≠0.
Определение. Квадратичной функцией называется функция, которую можно задать формулой вида у=ах2+bx+c, где х – независимая переменная, а, b и с – некоторые числа, причем а≠0.
Cлайд 5
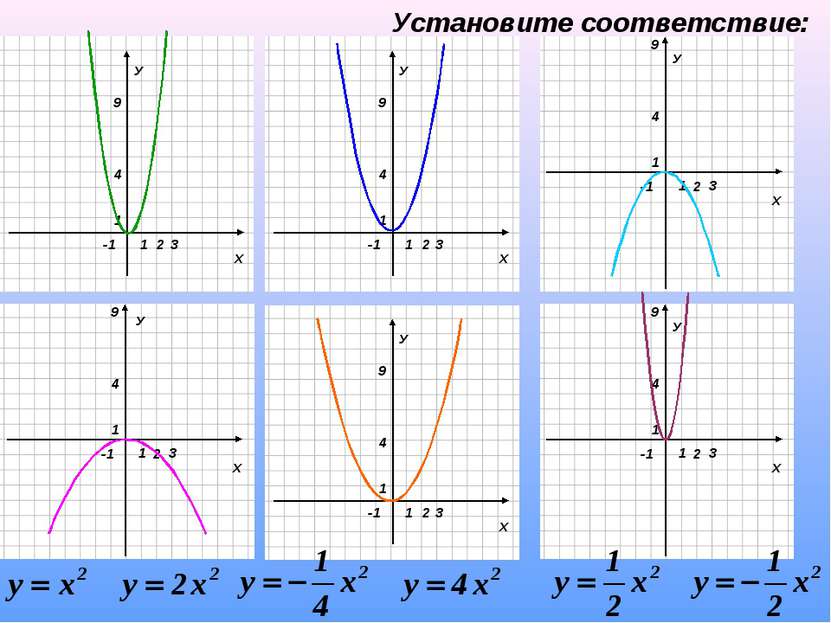
 Из приведенных примеров укажите те функции, которые являются квадратичными. Для квадратичных функций назовите коэффициенты.
Из приведенных примеров укажите те функции, которые являются квадратичными. Для квадратичных функций назовите коэффициенты.
Cлайд 11
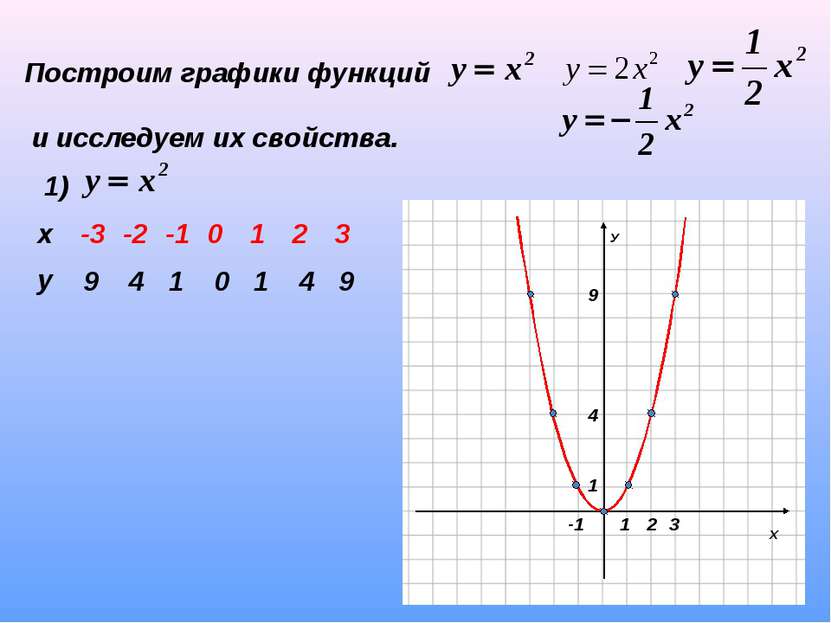
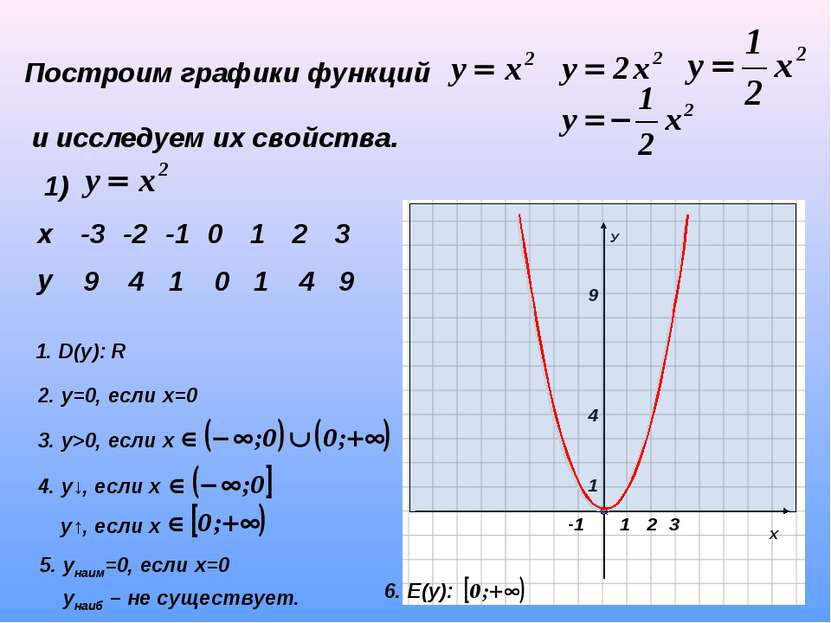
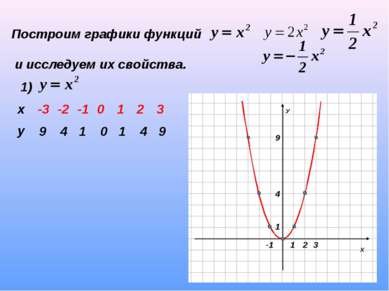
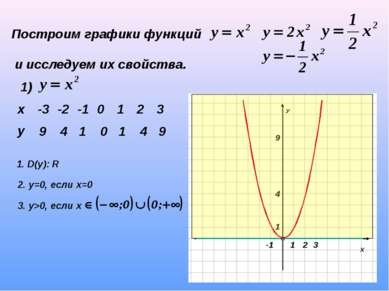 Построим графики функций и исследуем их свойства. 1) 9 4 1 0 1 4 9 1. D(y): R 2. у=0, если х=0 3. у>0, если х х -3 -2 -1 0 1 2 3 у
Построим графики функций и исследуем их свойства. 1) 9 4 1 0 1 4 9 1. D(y): R 2. у=0, если х=0 3. у>0, если х х -3 -2 -1 0 1 2 3 у
Cлайд 12
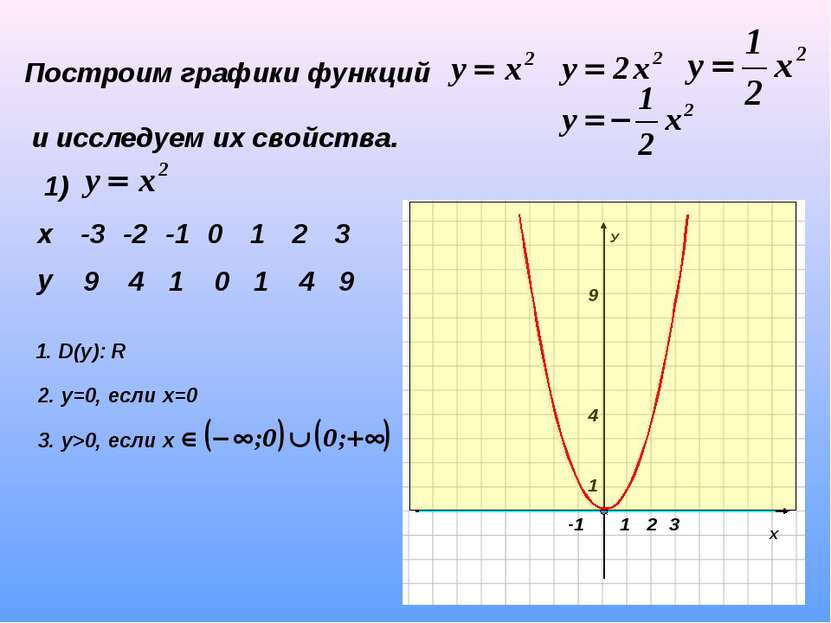
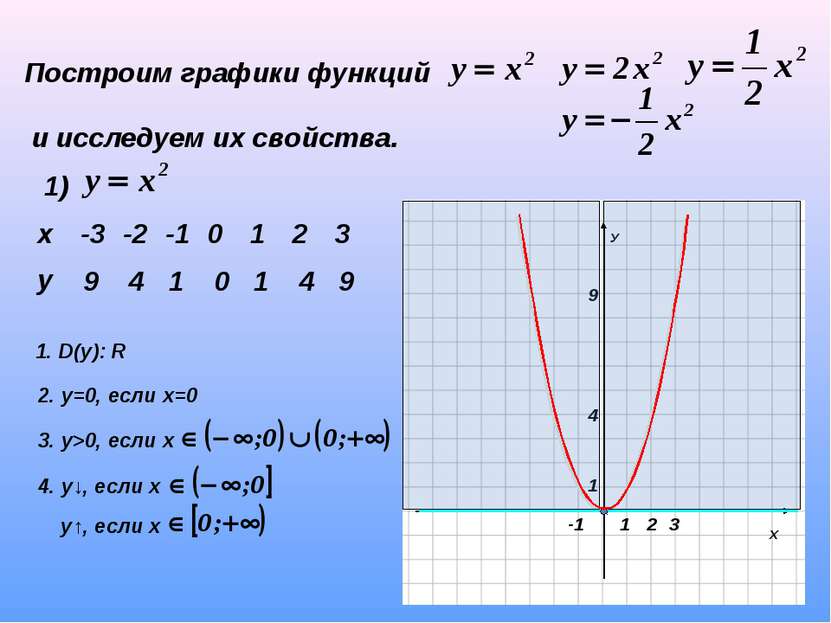
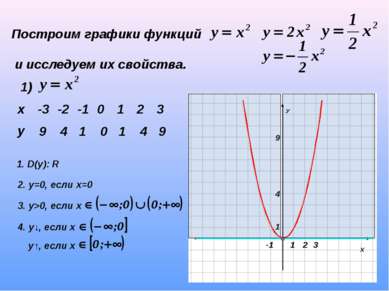 Построим графики функций и исследуем их свойства. 1) 9 4 1 0 1 4 9 1. D(y): R 2. у=0, если х=0 3. у>0, если х 4. у↓, если х у↑, если х х -3 -2 -1 0 1 2 3 у
Построим графики функций и исследуем их свойства. 1) 9 4 1 0 1 4 9 1. D(y): R 2. у=0, если х=0 3. у>0, если х 4. у↓, если х у↑, если х х -3 -2 -1 0 1 2 3 у
Cлайд 13
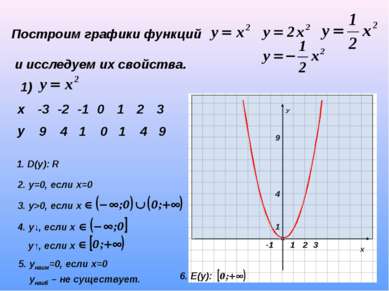 Построим графики функций и исследуем их свойства. 1) 9 4 1 0 1 4 9 1. D(y): R 2. у=0, если х=0 3. у>0, если х 4. у↓, если х у↑, если х 5. унаим=0, если х=0 унаиб – не существует. 6. Е(y): х -3 -2 -1 0 1 2 3 у
Построим графики функций и исследуем их свойства. 1) 9 4 1 0 1 4 9 1. D(y): R 2. у=0, если х=0 3. у>0, если х 4. у↓, если х у↑, если х 5. унаим=0, если х=0 унаиб – не существует. 6. Е(y): х -3 -2 -1 0 1 2 3 у
Cлайд 14
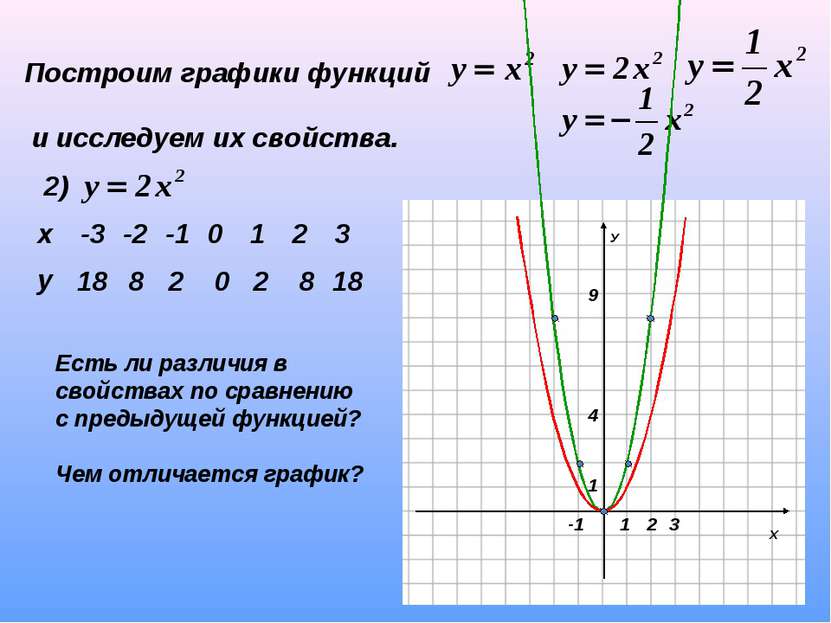
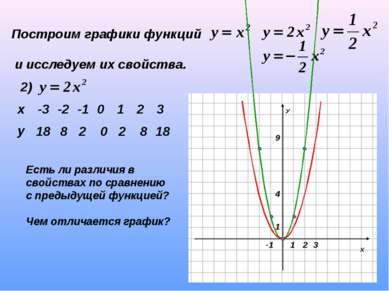 Построим графики функций и исследуем их свойства. 2) 18 8 2 0 2 8 18 Есть ли различия в свойствах по сравнению с предыдущей функцией? Чем отличается график? х -3 -2 -1 0 1 2 3 у
Построим графики функций и исследуем их свойства. 2) 18 8 2 0 2 8 18 Есть ли различия в свойствах по сравнению с предыдущей функцией? Чем отличается график? х -3 -2 -1 0 1 2 3 у
Cлайд 15
 График функции у=kx2 может быть получен из графика функции у=x2 путем растяжения его вдоль оси Оу в k раз (k-натуральное число).
График функции у=kx2 может быть получен из графика функции у=x2 путем растяжения его вдоль оси Оу в k раз (k-натуральное число).
Cлайд 16
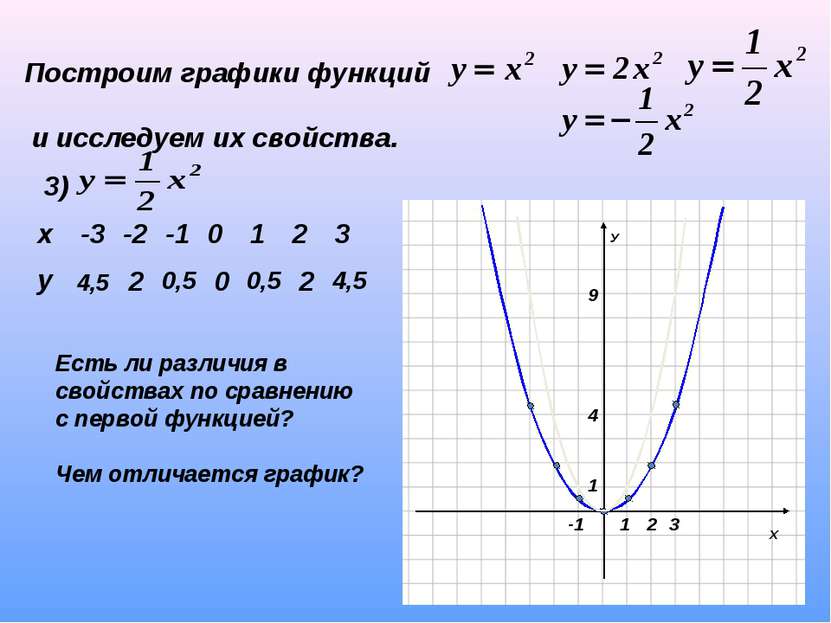
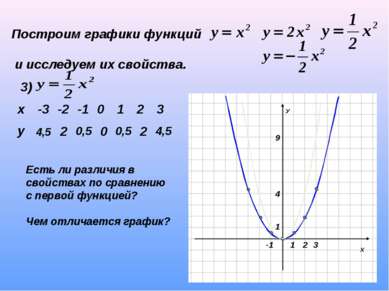 Построим графики функций и исследуем их свойства. 3) 4,5 2 0,5 0 0,5 2 4,5 Есть ли различия в свойствах по сравнению с первой функцией? Чем отличается график? х -3 -2 -1 0 1 2 3 у
Построим графики функций и исследуем их свойства. 3) 4,5 2 0,5 0 0,5 2 4,5 Есть ли различия в свойствах по сравнению с первой функцией? Чем отличается график? х -3 -2 -1 0 1 2 3 у
Cлайд 17
 График функции у= x2 может быть получен из графика функции у=x2 путем сжатия его вдоль оси Оу в k раз (k-натуральное число).
График функции у= x2 может быть получен из графика функции у=x2 путем сжатия его вдоль оси Оу в k раз (k-натуральное число).
Cлайд 18
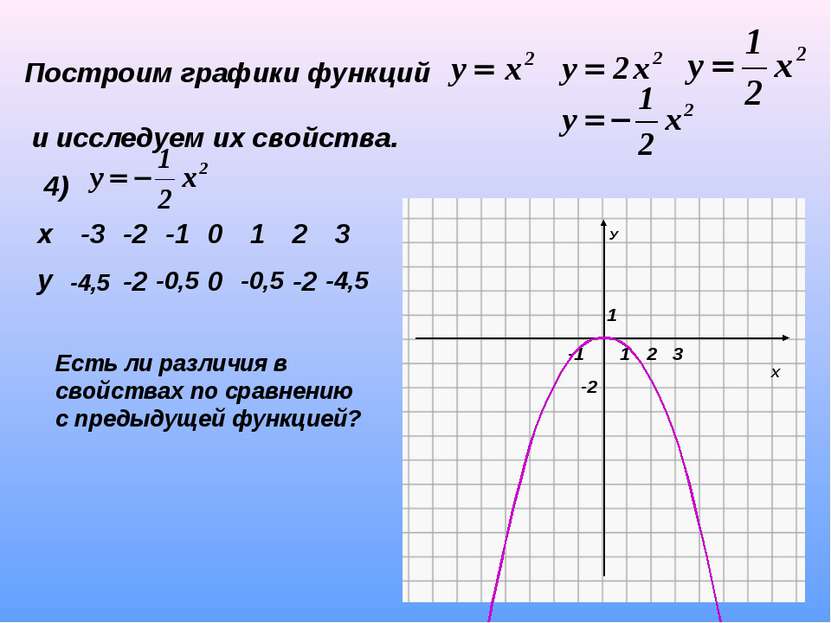
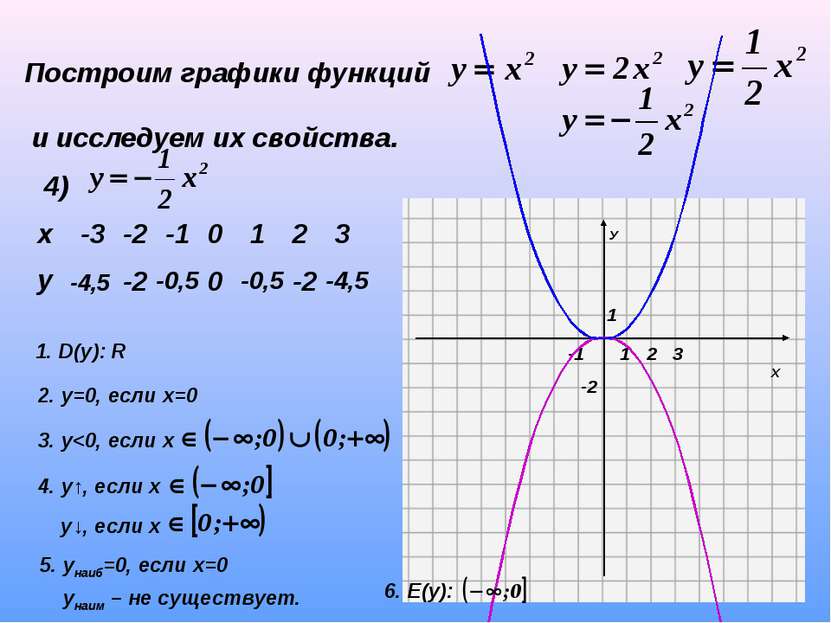
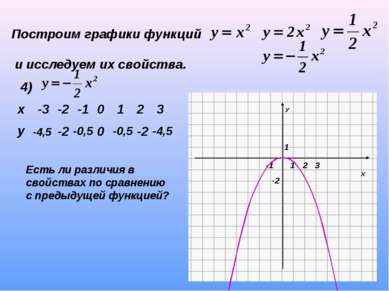 Построим графики функций и исследуем их свойства. 4) -4,5 -2 -0,5 0 -0,5 -2 -4,5 Есть ли различия в свойствах по сравнению с предыдущей функцией? х -3 -2 -1 0 1 2 3 у
Построим графики функций и исследуем их свойства. 4) -4,5 -2 -0,5 0 -0,5 -2 -4,5 Есть ли различия в свойствах по сравнению с предыдущей функцией? х -3 -2 -1 0 1 2 3 у
Cлайд 19
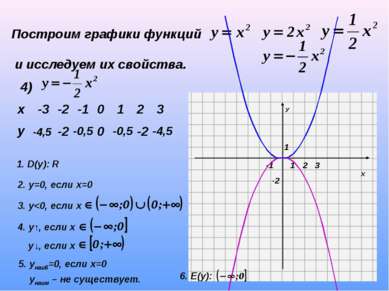 Построим графики функций и исследуем их свойства. 4) -4,5 -2 -0,5 0 -0,5 -2 -4,5 1. D(y): R 2. у=0, если х=0 3. у
Построим графики функций и исследуем их свойства. 4) -4,5 -2 -0,5 0 -0,5 -2 -4,5 1. D(y): R 2. у=0, если х=0 3. у