X
Код презентации скопируйте его
Призма и ее свойства
Скачать эту презентацию
Презентация на тему Призма и ее свойства
Скачать эту презентациюCлайд 1
ГОУ СПО «Димитровградский технический колледж» Тема: “Призма и ее свойства” Автор: Тихонов Никита Евгеньевич Руководитель: Кузьмина В. В. 2007 г.
Cлайд 2
Содержание Историческая справка Призма и ее свойства Решение задач Задачи для самостоятельной работы Литература
Cлайд 3
Еще в древности существовали два пути определения геометрических понятий. Первый вел от фигур высшего порядка к фигурам низшего. Такой точки зрения придерживался, в частности, Евклид, определяющий поверхность как границу тела, линию – как границу поверхности, концы же линии – как точки.
Cлайд 4
Второй путь ведет, наоборот, от фигур низшего измерения к фигурам высшего: движением точки образуется линия, аналогично из линий составляется поверхность и т. д. Одним из первых, который соединил обе эти точки зрения, был Герон Александрийский, писавший, что тело ограничивается поверхностью и вместе с этим может быть рассмотрено как образованное движением поверхности.
Cлайд 5
В появившихся позже на протяжении веков учебниках геометрии принималась за основу то одна, то другая, а иногда и обе вместе точки зрения.
Cлайд 6
Евклид употребляет термин «плоскость» как в широком смысле (Рассматривая ее неограниченно продолженной во все направления), так и в смысле конечной, ограниченной ее части, в частности грани, аналогично применению им термина «прямая» ( в широком смысле - бесконечная прямая и в узком – отрезок).
Cлайд 7
В XVIII в. Тейлор дал такое определение призмы: это многогранник, у которого все грани, кроме двух, параллельны одной прямой.
Cлайд 8
В настоящее время геометрия тесно переплетается со многими другими разделами математики. Одним из источников развития и образования новых понятий в геометрии, как и в других областях математики, являются современные задачи естествознания, физики и техники.
Cлайд 9
Термин “призма” греческого происхождения и буквально означает “отпиленное”
Cлайд 10
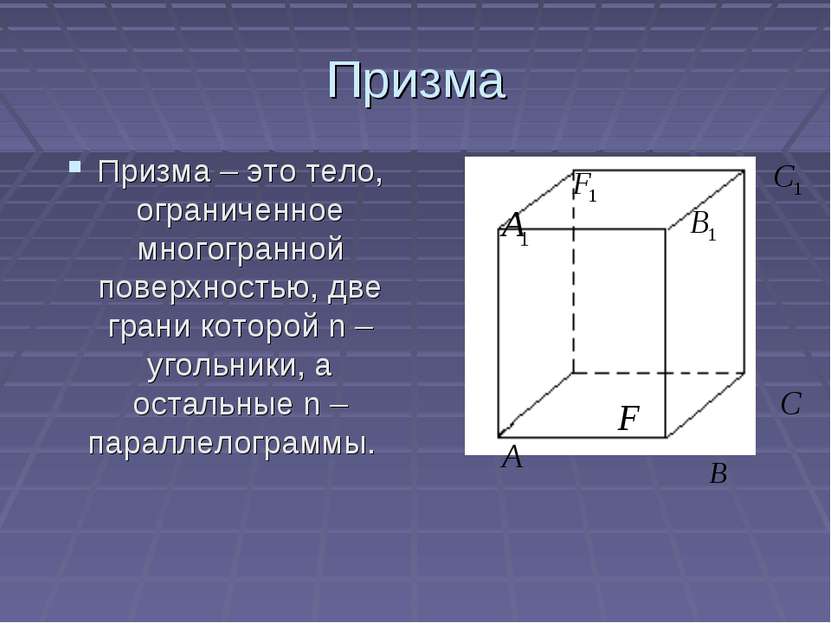
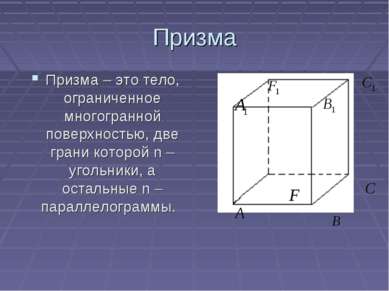Призма Призма – это тело, ограниченное многогранной поверхностью, две грани которой n – угольники, а остальные n – параллелограммы.
Cлайд 11
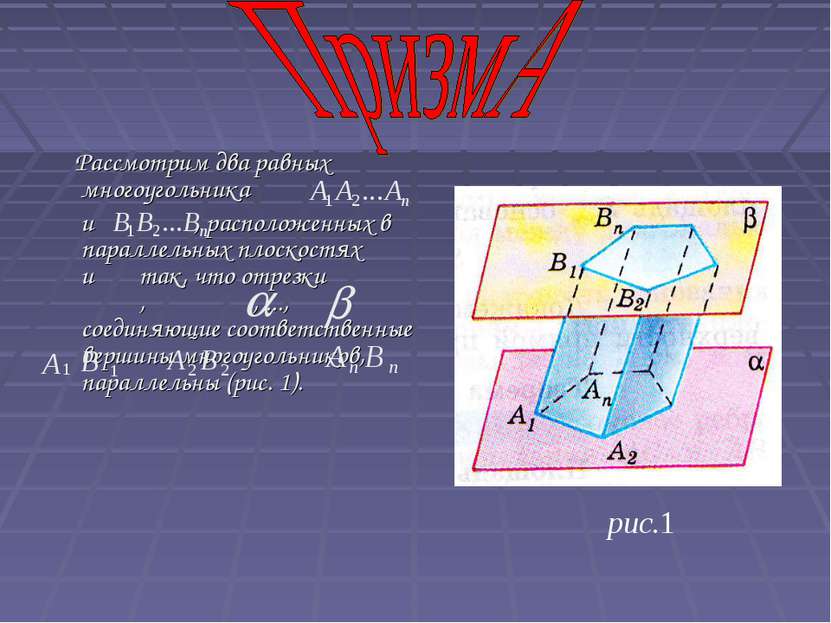
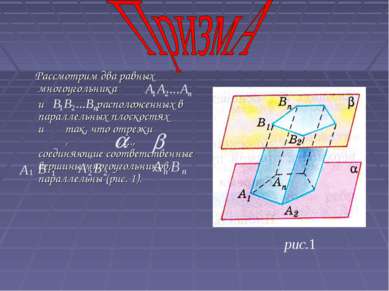Рассмотрим два равных многоугольника и , расположенных в параллельных плоскостях и так, что отрезки , , ..., , соединяющие соответственные вершины многоугольников, параллельны (рис. 1). 1 1 В А
Cлайд 12
Каждый из n четырехугольников является параллелограммов, так как имеет попарно параллельные противоположные стороны. Например, в четырехугольнике стороны и параллельны по условию, а стороны и - по свойству параллельных плоскостей, пересеченных третьей плоскостью (рис. 2).
Cлайд 13
Многоугольники и называются основаниями, а параллелограммы – боковыми гранями. Отрезки , называются боковыми ребрами призмы. Призму с основаниями и n - угольной призмой. ( рис. 3)
Cлайд 14
Призма называется правильной, если ее основания – правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники. На рисунке 4 изображена правильная шестиугольная призма. ( рис. 4 )
Cлайд 15
Поверхность призмы, таким образом, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней). Различают призмы треугольные, четырехугольные, пятиугольные и т.д., в зависимости от числа вершин основания.
Cлайд 16
Поверхность многогранника состоит из конечного числа многоугольников. Площадь поверхности многогранника есть сумма площадей всех его граней. Площадь поверхности призм ( ) равна сумме площадей ее боковых граней (площади боковой поверхности) ( ) и площадей двух оснований (2Sосн) - равных многоугольников:
Cлайд 17
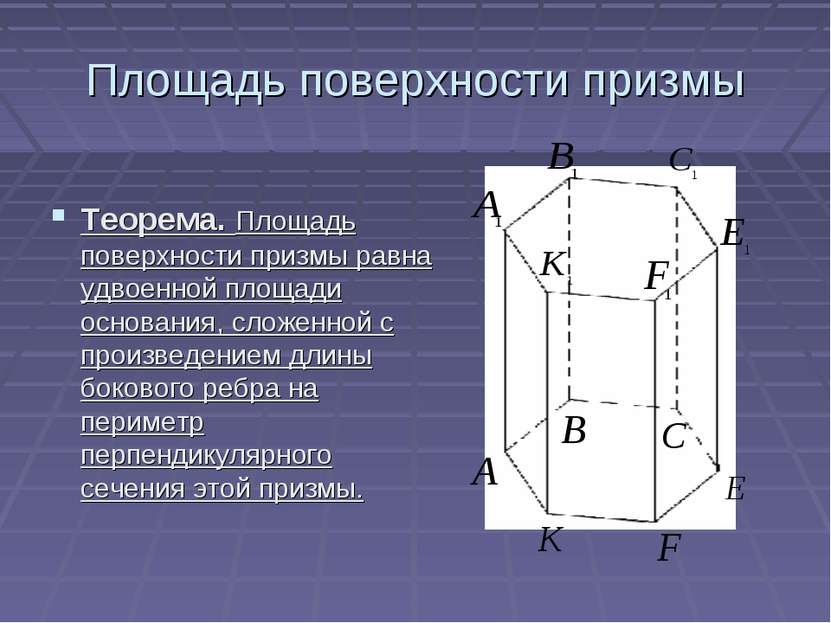
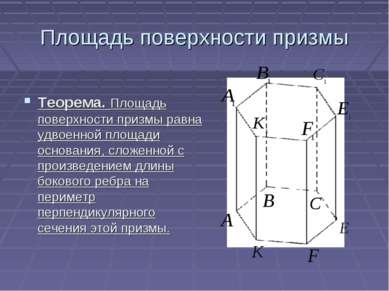Площадь поверхности призмы Теорема. Площадь поверхности призмы равна удвоенной площади основания, сложенной с произведением длины бокового ребра на периметр перпендикулярного сечения этой призмы.
Cлайд 18
Боковые грани прямой призмы – прямоугольники, основания которых – стороны призмы, а высоты равны высоте h призмы. Площадь боковой поверхности призмы равна сумме произведений сторон основания на высоту h. Вынося множитель h за скобки, получим в скобках сумму сторон основания призмы, т.е. его периметр Р. Итак, Sбок=Рh. Теорема доказана.
Cлайд 19
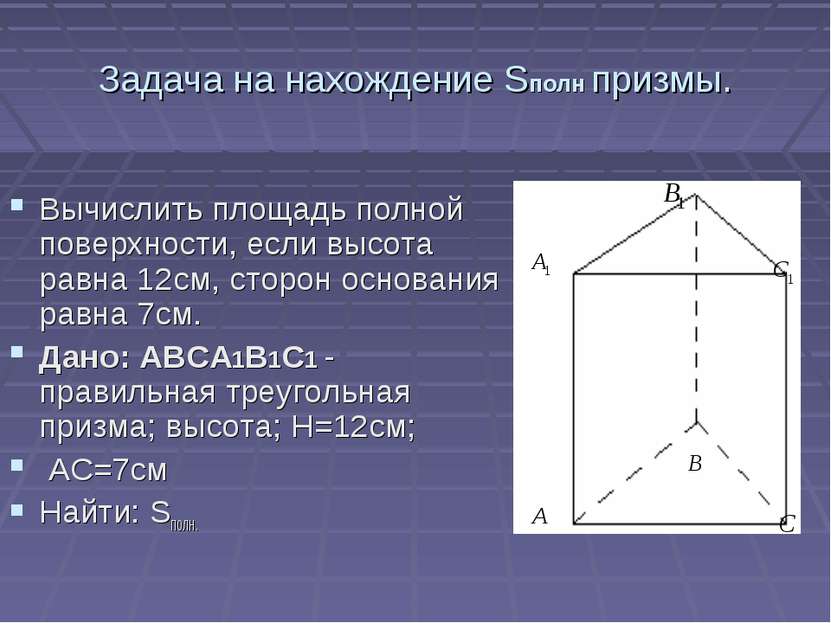
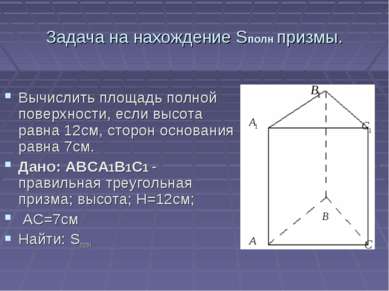Задача на нахождение Sполн призмы. Вычислить площадь полной поверхности, если высота равна 12см, сторон основания равна 7см. Дано: ABCA1B1C1 - правильная треугольная призма; высота; Н=12см; АС=7см Найти: Sполн.
Cлайд 20
Решение: Ответ:
Cлайд 21
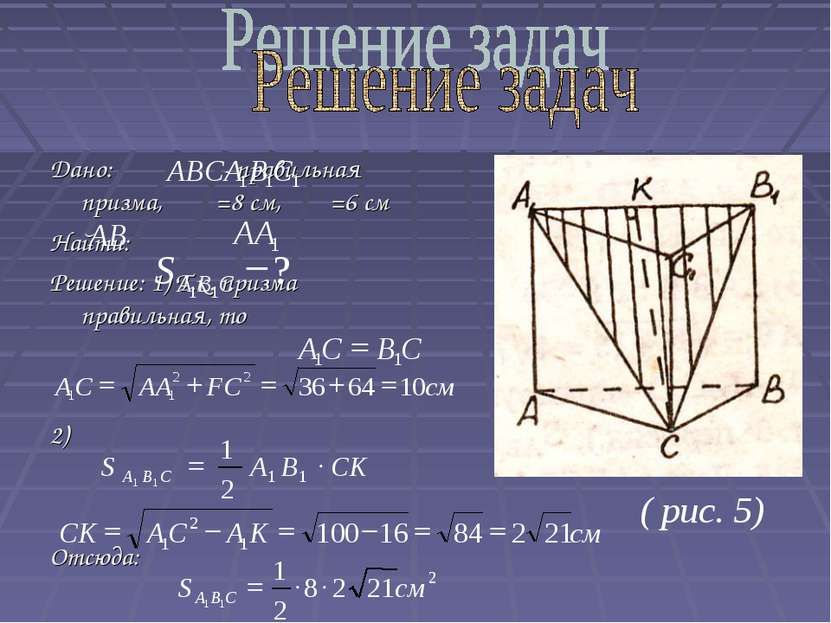
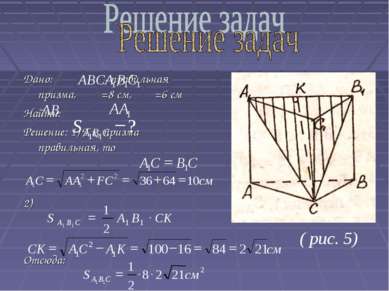Дано: - правильная призма, =8 см, =6 см Найти: Решение: 1) Т.к. призма правильная, то 2) Отсюда: ( рис. 5)
Cлайд 22
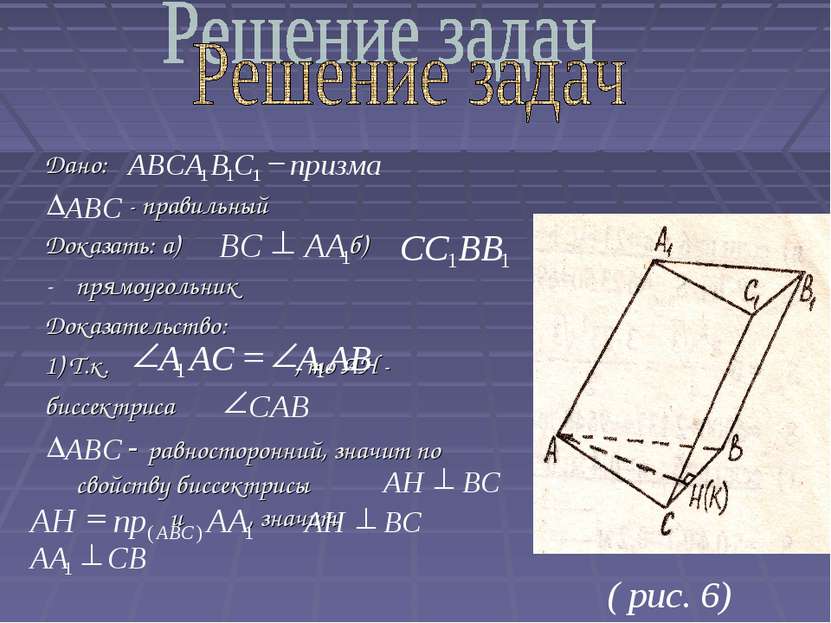
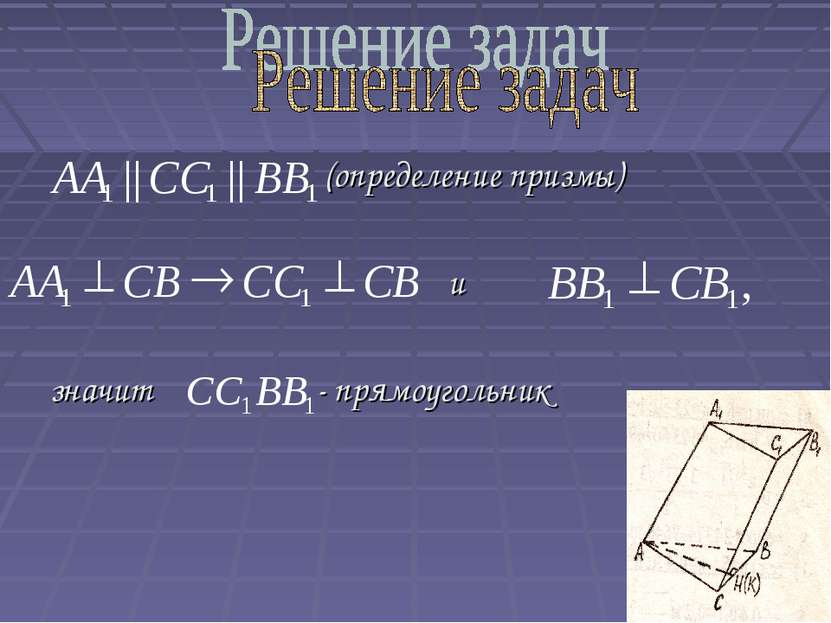
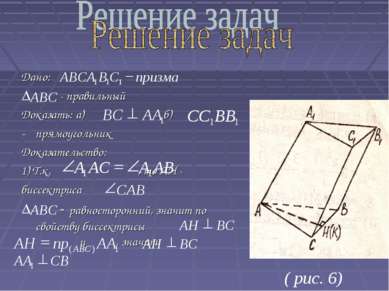Дано: - правильный Доказать: а) б) прямоугольник Доказательство: 1) Т.к. , то АН - биссектриса - равносторонний, значит по свойству биссектрисы и , значит ( рис. 6)
Cлайд 23
(определение призмы) и значит - прямоугольник
Cлайд 24
Докажите, что: а) у прямой призмы все боковые грани – прямоугольники; б) у правильной призмы все боковые грани – равные прямоугольники. Сторона правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдете площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
Cлайд 25
Основаниями прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 см и высотой 8 см. Найдите двухгранные углы при боковых ребрах призмы. Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол 30`. Найдите угол между диагональю и плоскостью основания.
Cлайд 26
Дадаян А. А. Математика: Учебник - М.: ИНФРА - М, 2006 Геометрия 10 - 11; Учеб. Для общеобразовательных учреждений под ред. А. Н. Тихонова - М.: Просвещение, 2001 Internet ресурсы: www.5ballov.ru www.4students.ru
