X
Код презентации скопируйте его
Подготовка к ЕГЭ Задание В8
Скачать эту презентацию
![4. Непрерывная функция у = f(x) задана на отрезке [a;b] На рисунке изображен ...](https://bigslide.ru/images/40/39447/831/img5.jpg "4. Непрерывная функция у = f(x) задана на отрезке [a;b] На рисунке изображен ...")
Презентация на тему Подготовка к ЕГЭ Задание В8
Скачать эту презентациюCлайд 1
Подготовка к ЕГЭ Задание В 8 Липлянская Татьяна Геннадьевна, учитель математики МОБУ «СОШ №3» Г Ясный Оренбургская область
Cлайд 2
В8 Умения выполнять действия с функциями (геометрический и физический смысл производной)
Cлайд 3
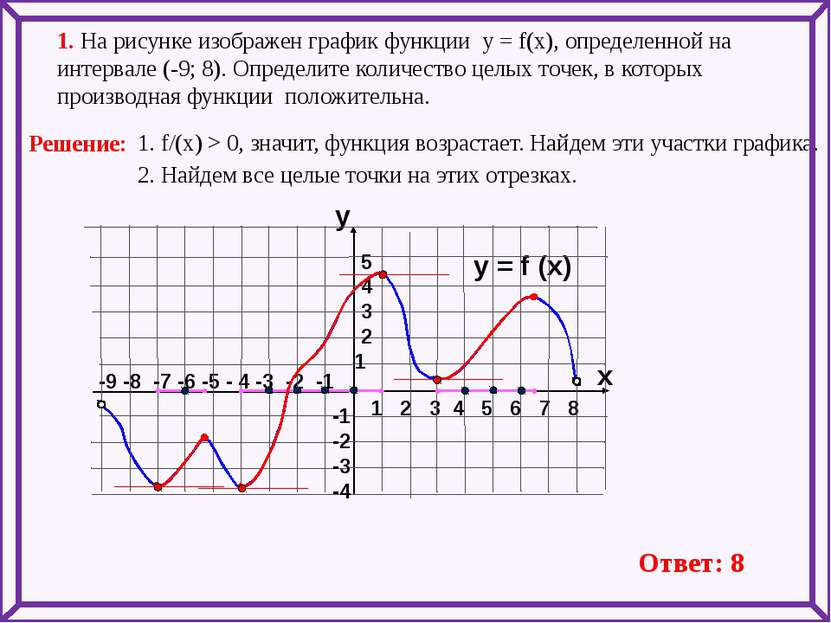
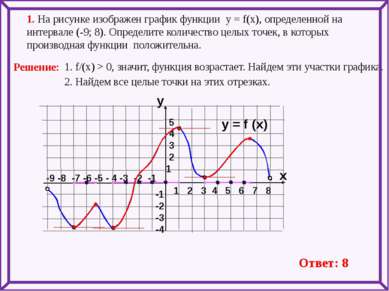-9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6 7 8 1. На рисунке изображен график функции у = f(x), определенной на интервале (-9; 8). Определите количество целых точек, в которых производная функции положительна. y = f (x) y x 5 4 3 2 1 -1 -2 -3 -4 1. f/(x) > 0, значит, функция возрастает. Найдем эти участки графика. 2. Найдем все целые точки на этих отрезках. Ответ: 8 Решение:
Cлайд 4
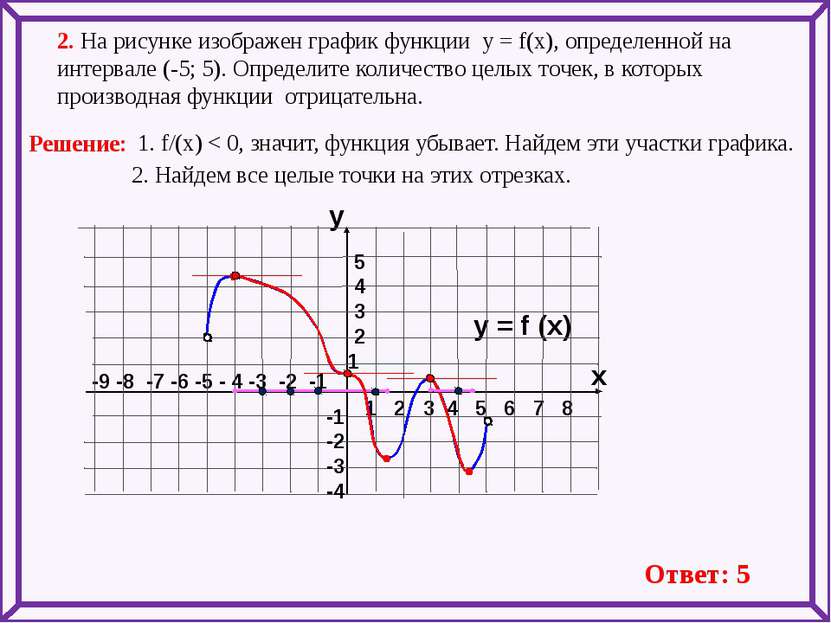
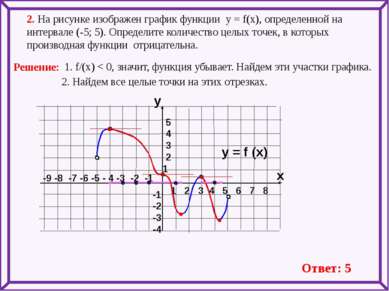-9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6 7 8 2. На рисунке изображен график функции у = f(x), определенной на интервале (-5; 5). Определите количество целых точек, в которых производная функции отрицательна. y = f (x) y x 5 4 3 2 1 -1 -2 -3 -4 1. f/(x) < 0, значит, функция убывает. Найдем эти участки графика. 2. Найдем все целые точки на этих отрезках. Ответ: 5 Решение:
Cлайд 5
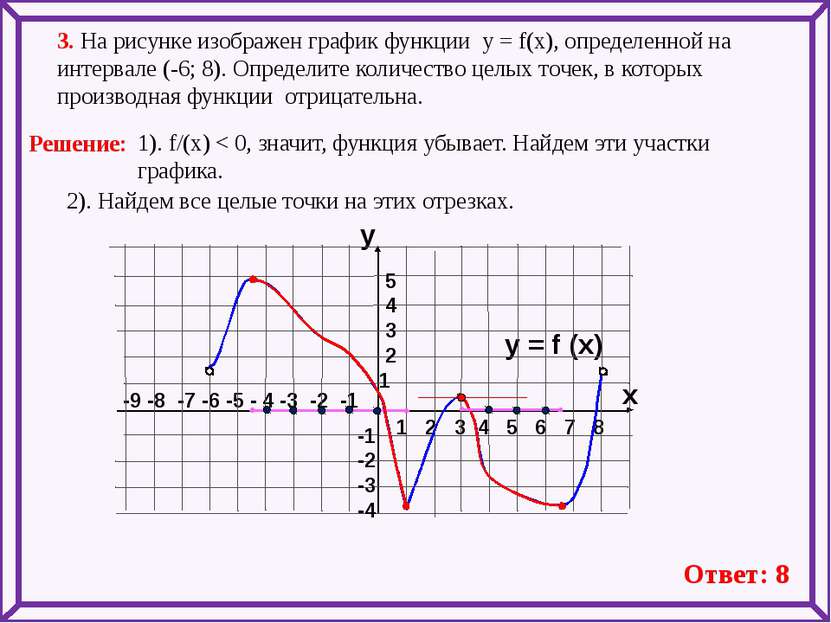
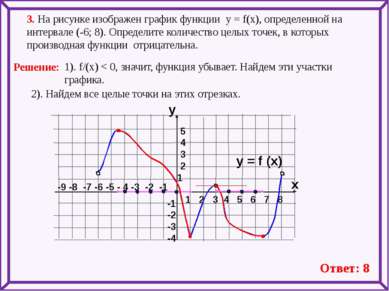-9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6 7 8 3. На рисунке изображен график функции у = f(x), определенной на интервале (-6; 8). Определите количество целых точек, в которых производная функции отрицательна. y = f (x) y x 5 4 3 2 1 -1 -2 -3 -4 1). f/(x) < 0, значит, функция убывает. Найдем эти участки графика. 2). Найдем все целые точки на этих отрезках. Ответ: 8 Решение:
Cлайд 6
![4. Непрерывная функция у = f(x) задана на отрезке [a;b] На рисунке изображен ...](https://bigslide.ru/images/40/39447/960/img5.jpg "4. Непрерывная функция у = f(x) задана на отрезке [a;b] На рисунке изображен ...")
4. Непрерывная функция у = f(x) задана на отрезке [a;b] На рисунке изображен ее график. В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох. y = f(x) y x Ответ: 5 a b http://mathege.ru:8080/or/ege/Main?view=TrainArchive
Cлайд 7
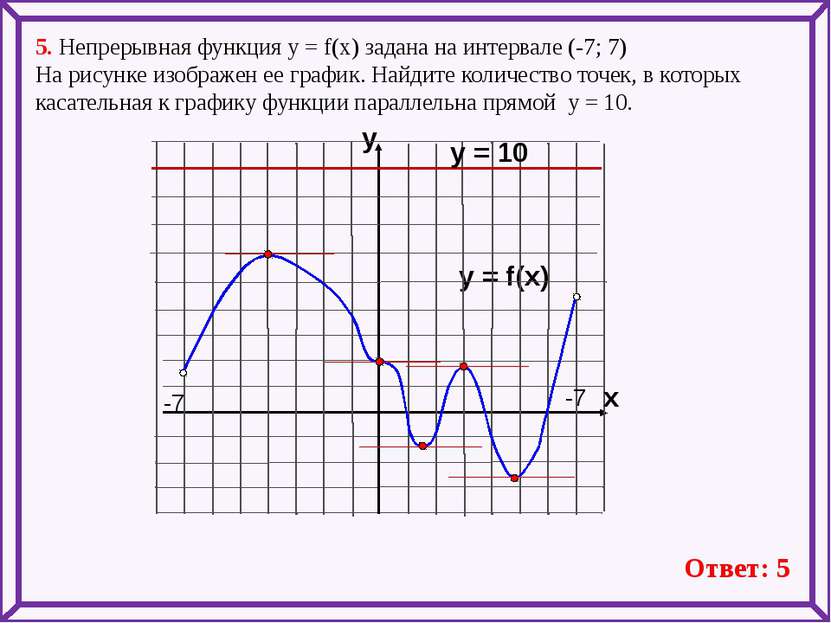
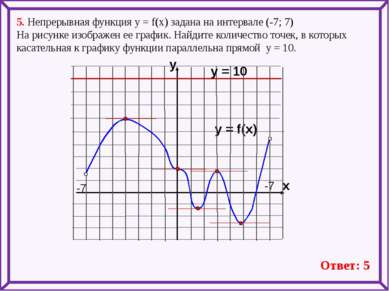5. Непрерывная функция у = f(x) задана на интервале (-7; 7) На рисунке изображен ее график. Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 10. y = f(x) y x -7 -7 Ответ: 5 y = 10
Cлайд 8
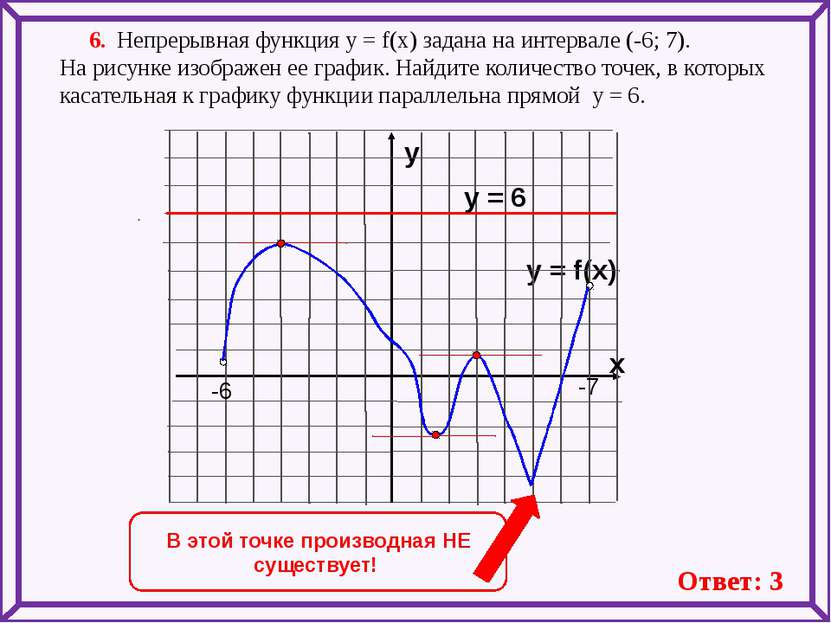
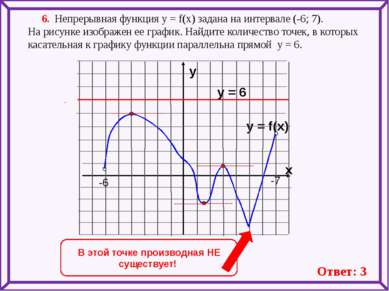6. Непрерывная функция у = f(x) задана на интервале (-6; 7). На рисунке изображен ее график. Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6. y = f(x) y x -6 -7 . В этой точке производная НЕ существует! Ответ: 3 y = 6
Cлайд 9
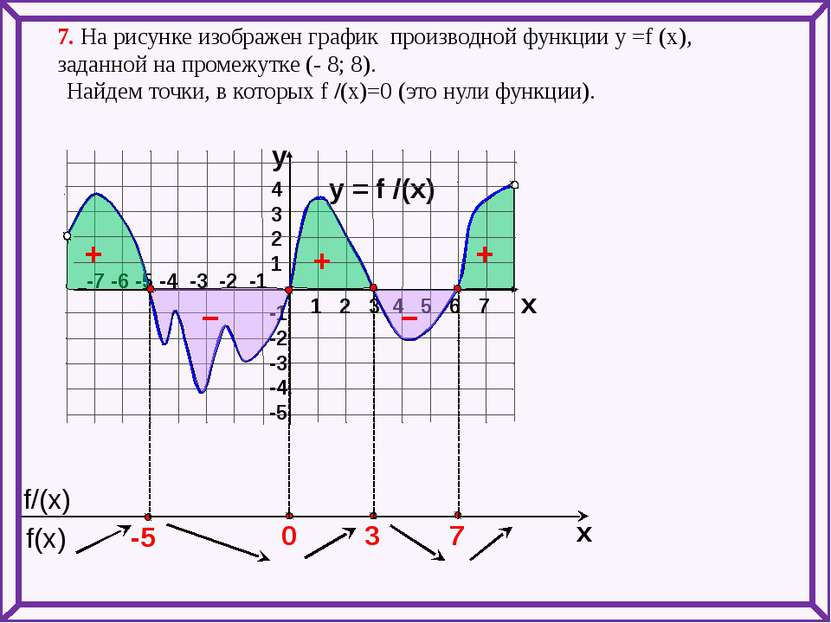
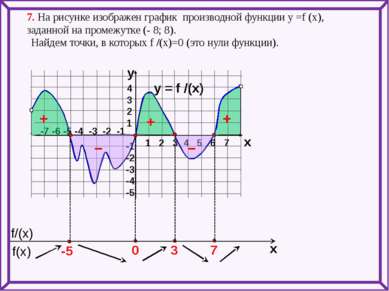7. На рисунке изображен график производной функции у =f (x), заданной на промежутке (- 8; 8). y = f /(x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 y x Найдем точки, в которых f /(x)=0 (это нули функции). + – – + + f(x) f/(x) x
Cлайд 10
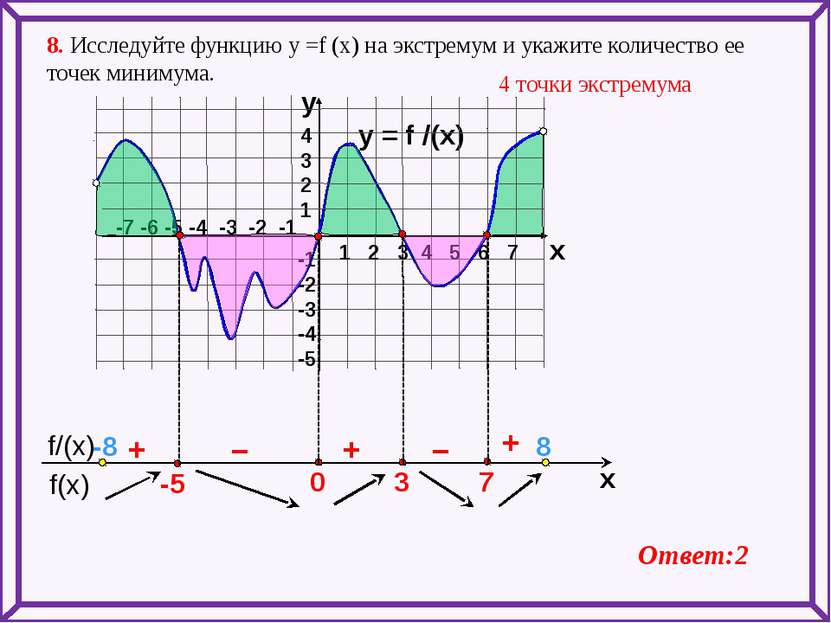
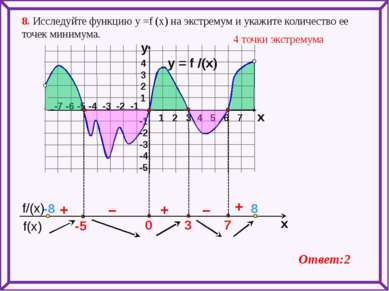y = f /(x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + 8. Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума. 4 точки экстремума Ответ:2 -8 8 f(x) f/(x) x
Cлайд 11
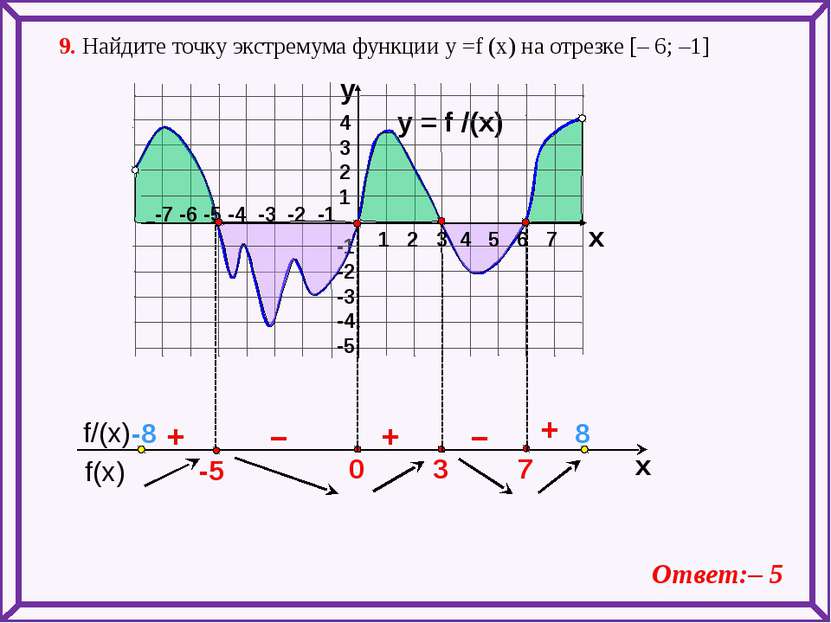
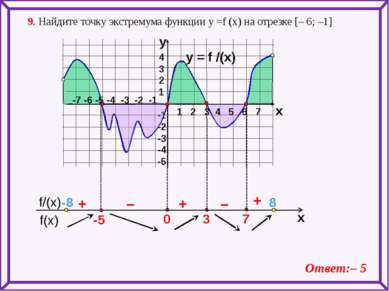y = f /(x) 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + 9. Найдите точку экстремума функции у =f (x) на отрезке [– 6; –1] Ответ:– 5 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -8 8 f(x) f/(x) x 7 -5
Cлайд 12
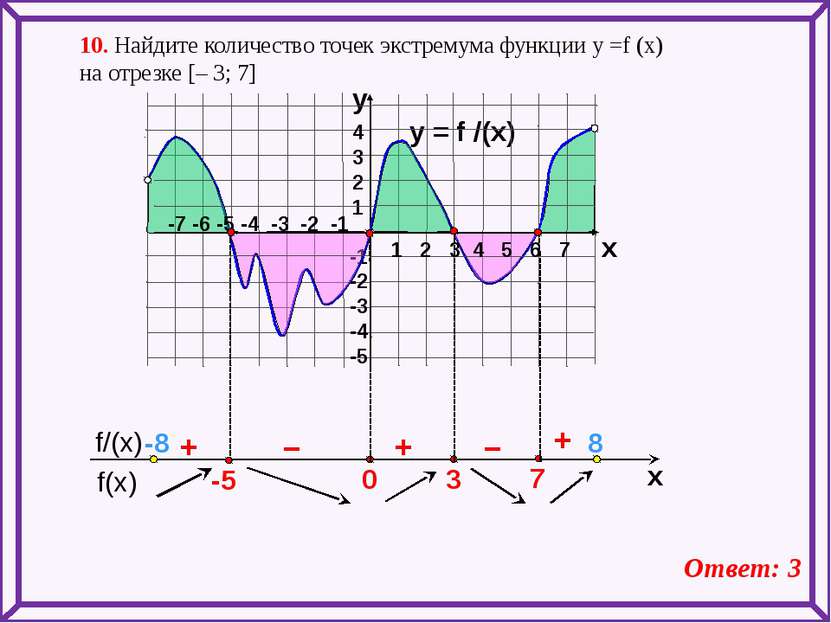
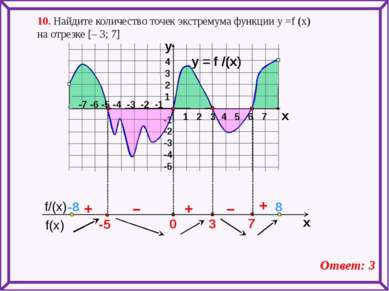y = f /(x) 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + 10. Найдите количество точек экстремума функции у =f (x) на отрезке [– 3; 7] Ответ: 3 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -8 8 f(x) f/(x) x -5 7
Cлайд 13
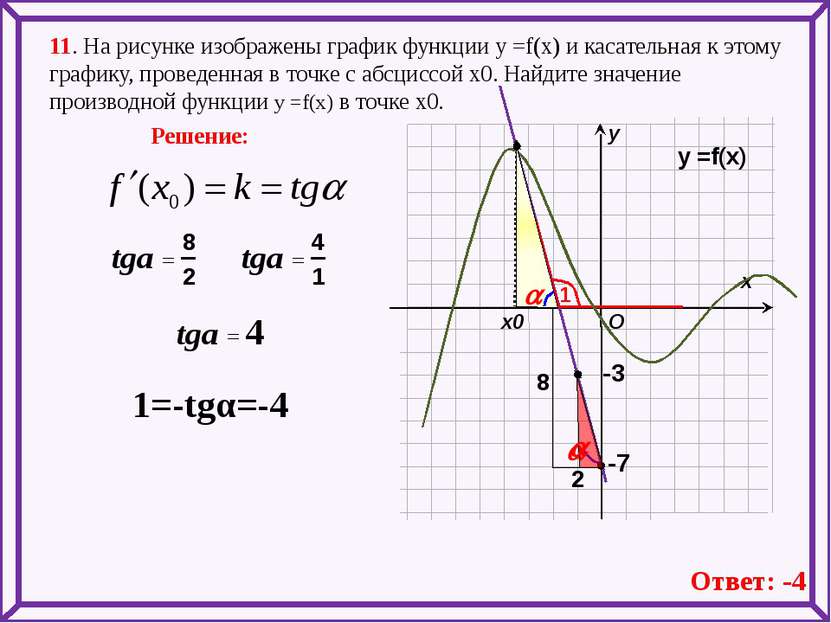
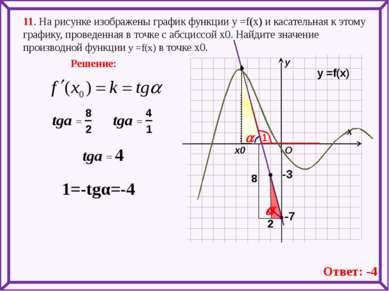11. На рисунке изображены график функции у =f(x) и касательная к этому графику, проведенная в точке с абсциссой х0. Найдите значение производной функции у =f(x) в точке х0. х х0 у Решение: O у =f(x) -3 -7 1=-tgα=-4 Ответ: -4 a 1 tga = a a tga = tga = 4
Cлайд 14
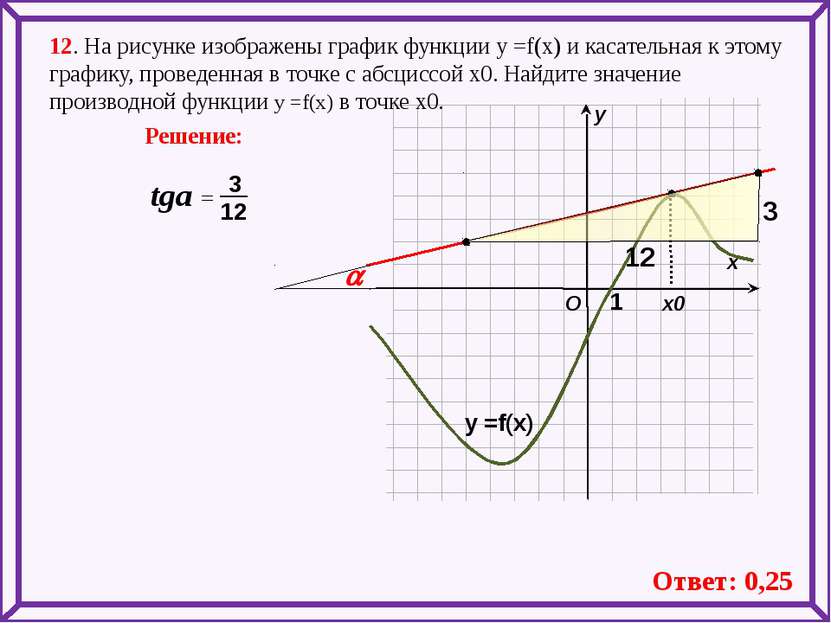
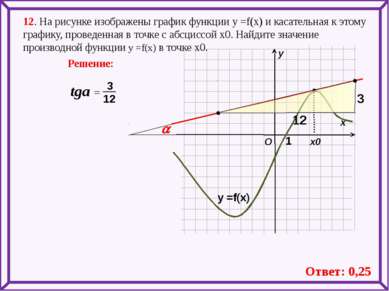12. На рисунке изображены график функции у =f(x) и касательная к этому графику, проведенная в точке с абсциссой х0. Найдите значение производной функции у =f(x) в точке х0. х х0 у Решение: O у =f(x) 1 a Ответ: 0,25 a 3 12 12 3 tga =
Cлайд 15
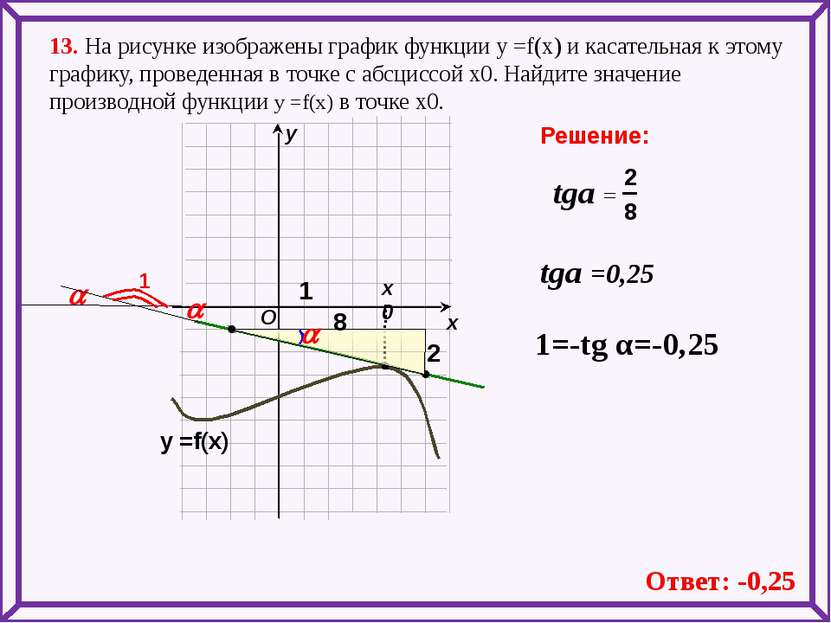
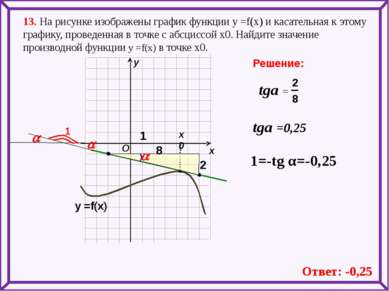13. На рисунке изображены график функции у =f(x) и касательная к этому графику, проведенная в точке с абсциссой х0. Найдите значение производной функции у =f(x) в точке х0. х х0 у Решение: O у =f(x) 1 a a Ответ: -0,25 tga =0,25 1=-tg α=-0,25 tga = 2 8
Cлайд 16
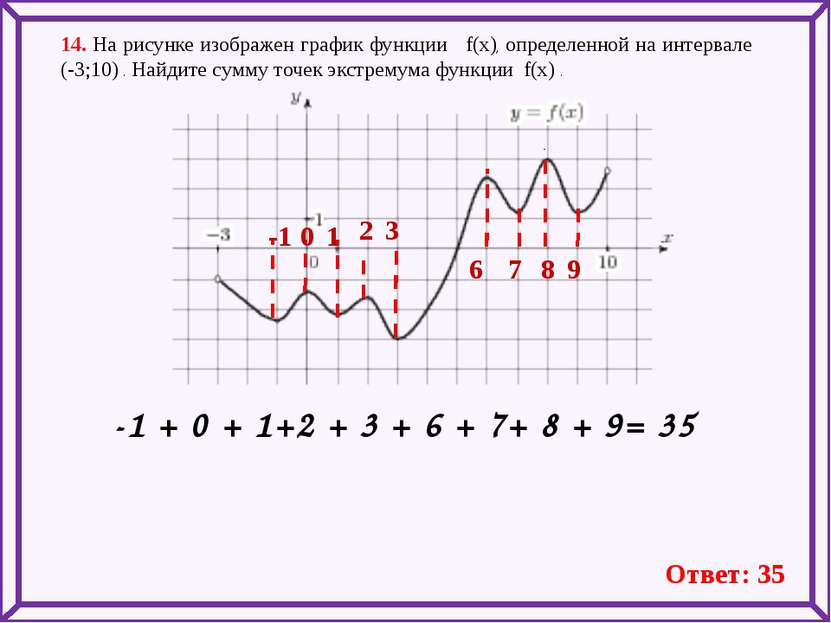
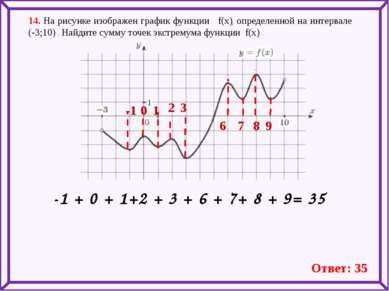14. На рисунке изображен график функции f(x), определенной на интервале (-3;10) . Найдите сумму точек экстремума функции f(x) . -1 0 1 3 6 7 8 9 -1 + 0 + 1+2 + 3 + 6 + 7+ 8 + 9= 35 Ответ: 35 2
Cлайд 17
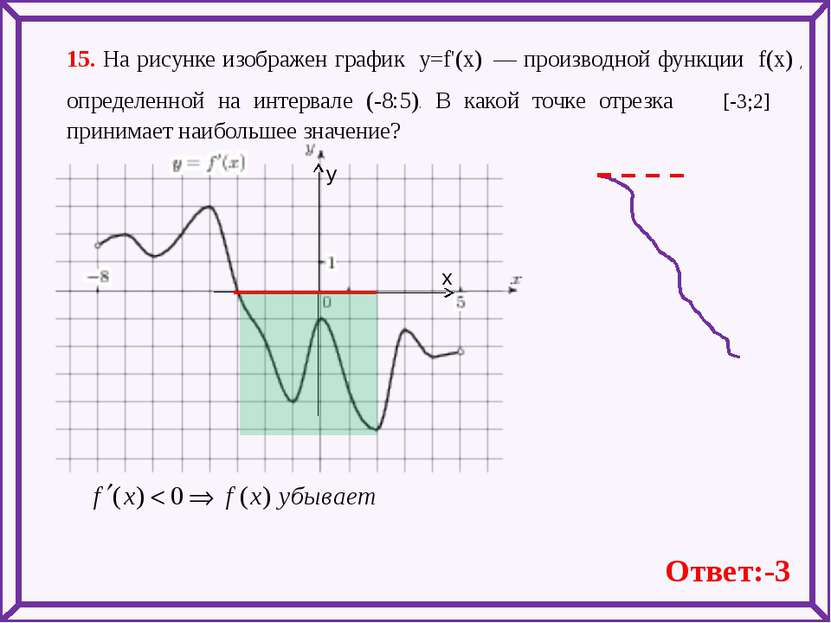
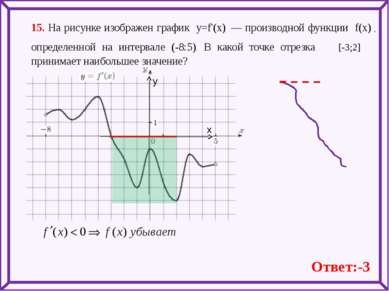15. На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-8:5). В какой точке отрезка [-3;2] принимает наибольшее значение? Ответ:-3 х у
Cлайд 18
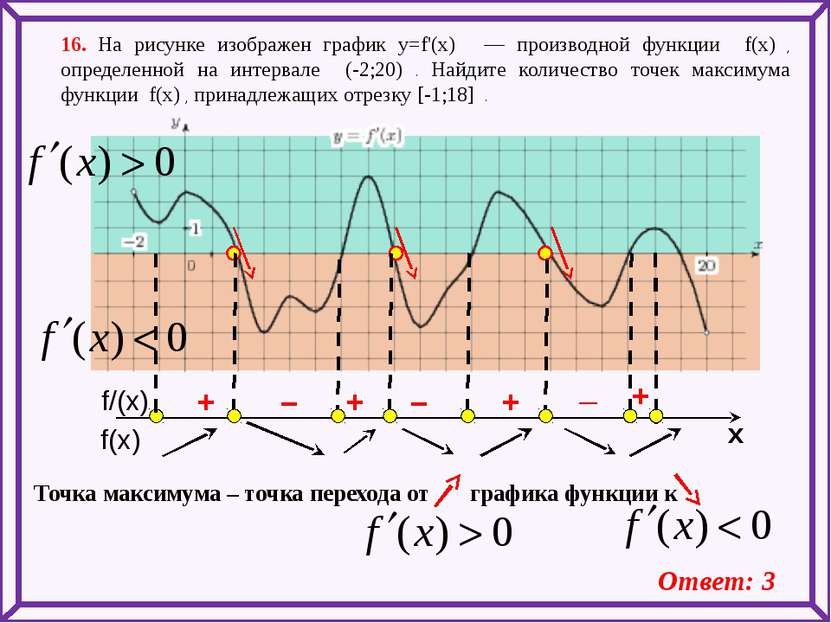
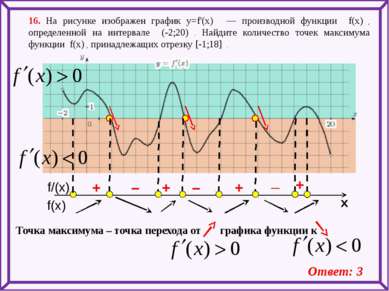16. На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-2;20) . Найдите количество точек максимума функции f(x) , принадлежащих отрезку [-1;18] . Ответ: 3 _ – – + + + + Точка максимума – точка перехода от графика функции к f(x) f/(x) x
Cлайд 19
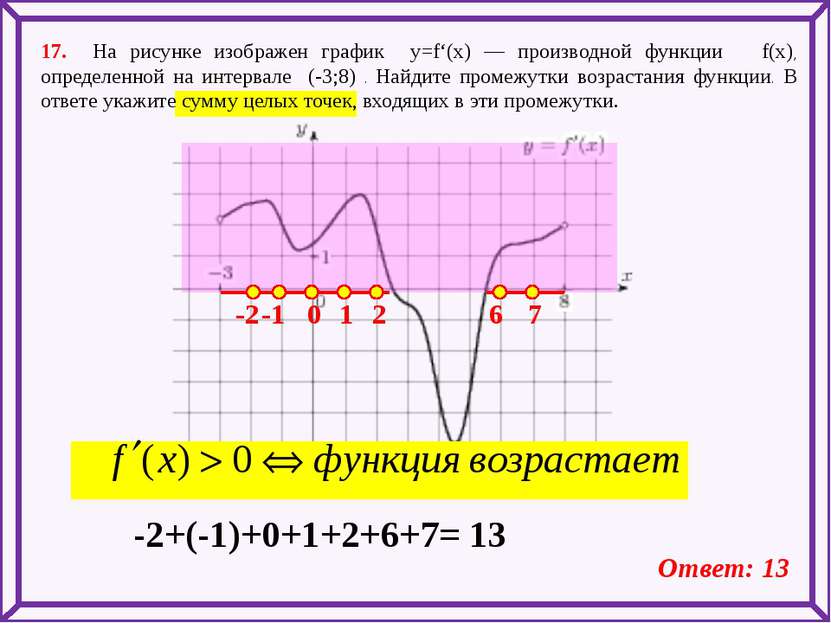
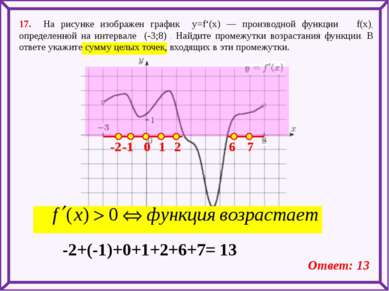17. На рисунке изображен график y=f‘(x) — производной функции f(x), определенной на интервале (-3;8) . Найдите промежутки возрастания функции. В ответе укажите сумму целых точек, входящих в эти промежутки. -2 -1 0 1 2 6 7 -2+(-1)+0+1+2+6+7= 13 Ответ: 13
Cлайд 20
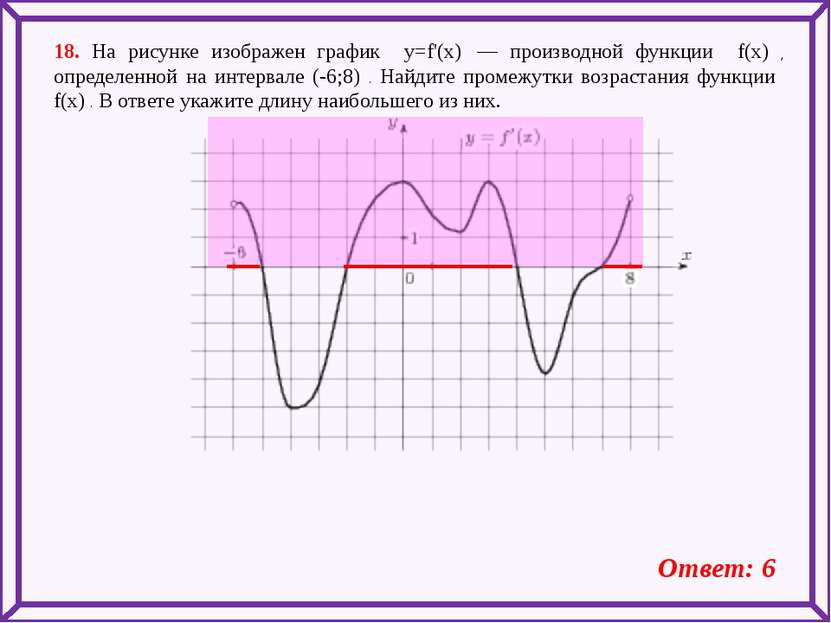
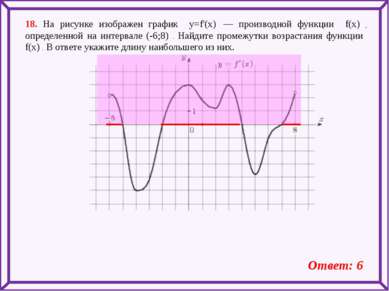18. На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-6;8) . Найдите промежутки возрастания функции f(x) . В ответе укажите длину наибольшего из них. Ответ: 6
Cлайд 21
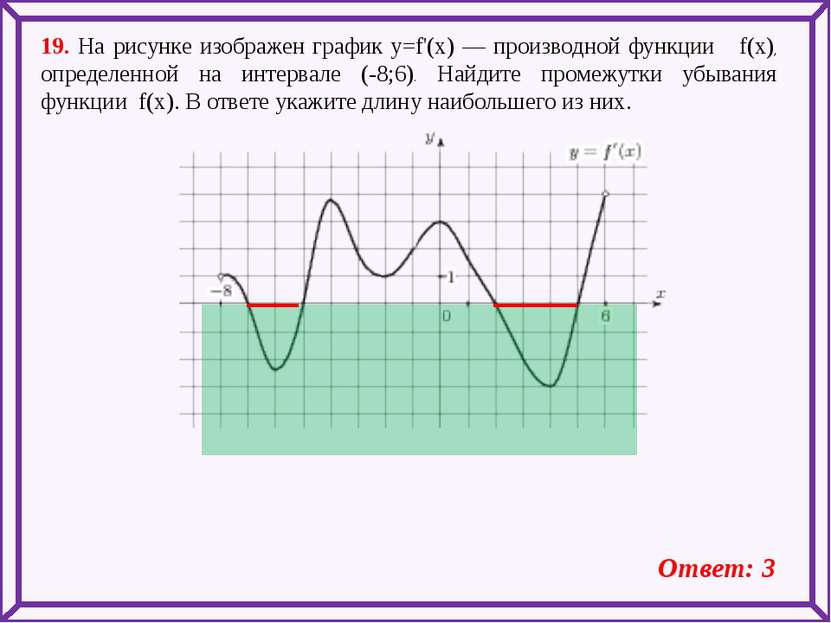
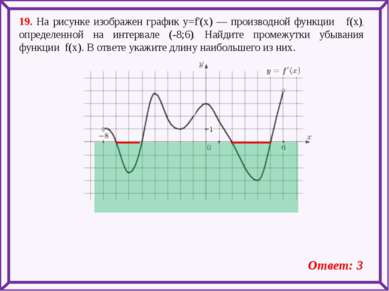19. На рисунке изображен график y=f'(x) — производной функции f(x), определенной на интервале (-8;6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них. Ответ: 3
Cлайд 22
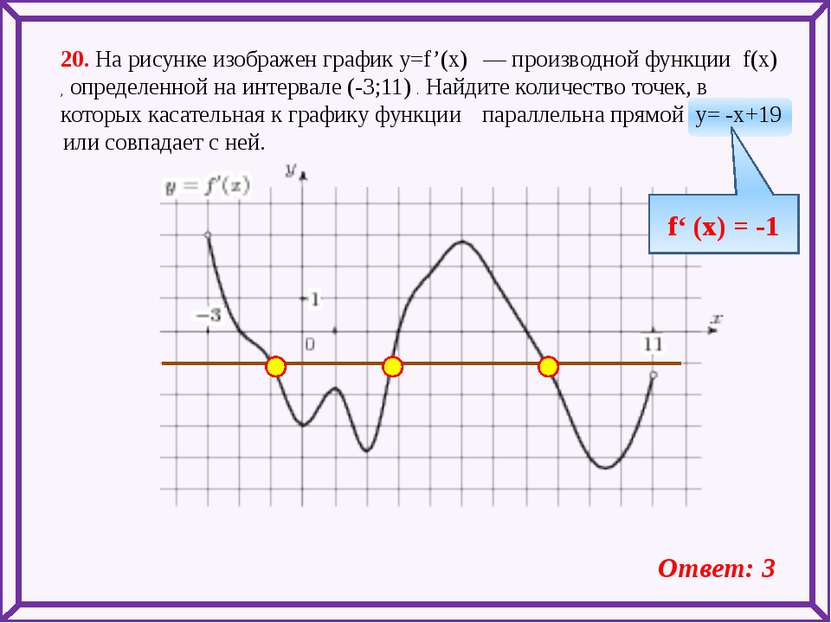
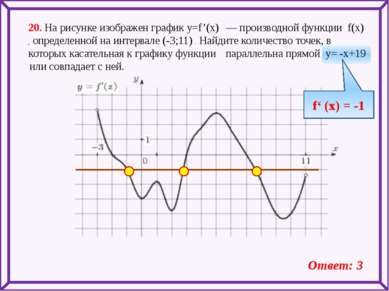20. На рисунке изображен график y=f’(x) — производной функции f(x) , определенной на интервале (-3;11) . Найдите количество точек, в которых касательная к графику функции параллельна прямой y= -x+19 или совпадает с ней. f‘ (x) = -1 Ответ: 3
Cлайд 23
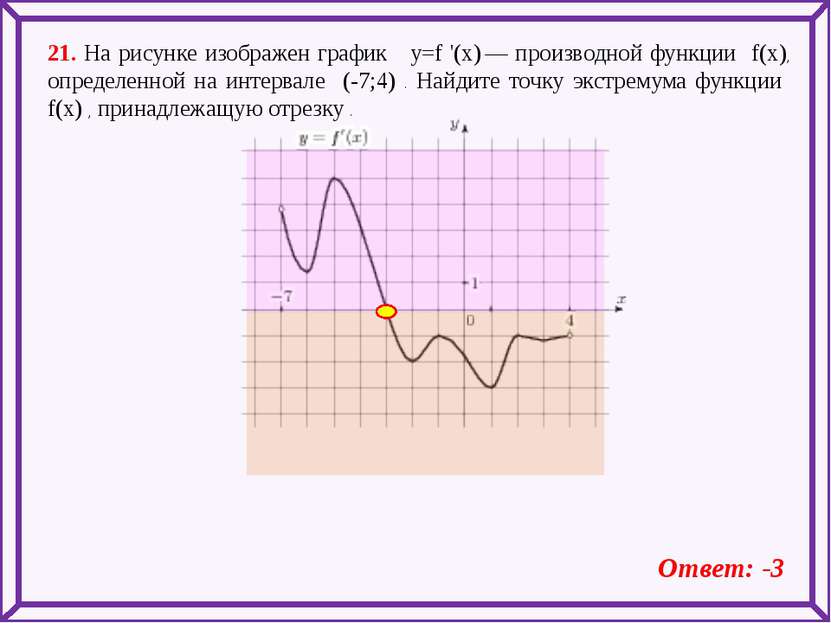
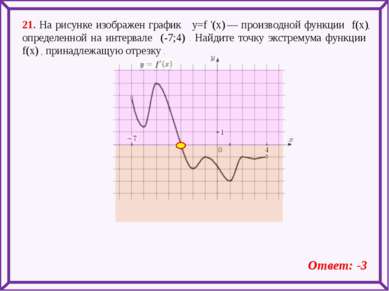21. На рисунке изображен график y=f '(x) — производной функции f(x), определенной на интервале (-7;4) . Найдите точку экстремума функции f(x) , принадлежащую отрезку . Ответ: -3
Cлайд 24
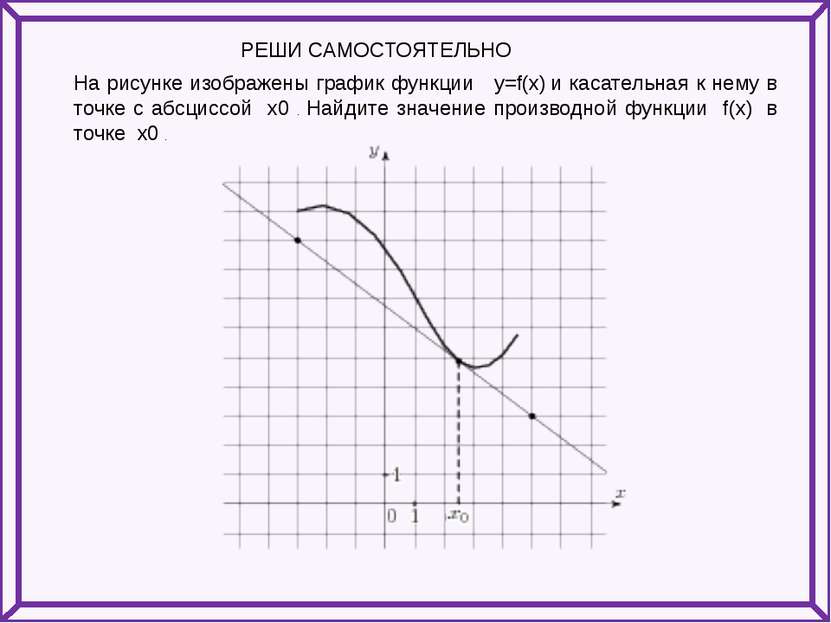
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 . РЕШИ САМОСТОЯТЕЛЬНО
Cлайд 25
На рисунке изображен график функции y=f(x) , определенной на интервале . Найдите количество точек, в которых производная функции равна 0 .
Cлайд 26
Материал с открытого банка заданий mathege.ru
