X
Код презентации скопируйте его
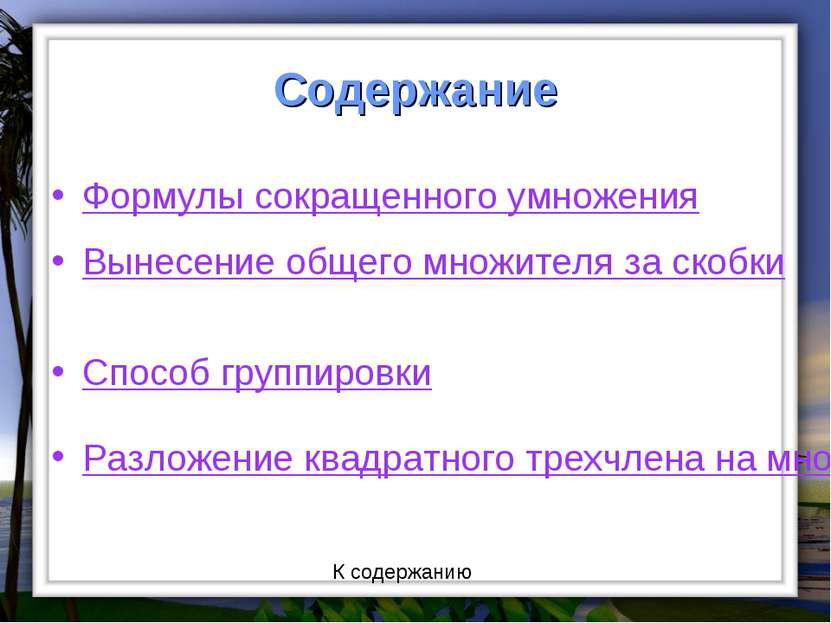
Разложение многочлена на множители с помощью комбинации различных приемов
Скачать эту презентацию
Презентация на тему Разложение многочлена на множители с помощью комбинации различных приемов
Скачать эту презентациюCлайд 1
Разложение многочлена на множители с помощью комбинации различных приемов 7 класс
Cлайд 2
Содержание Формулы сокращенного умножения Вынесение общего множителя за скобки Способ группировки Разложение квадратного трехчлена на множители К содержанию
Cлайд 3
Формулы сокращенного умножения
Cлайд 4
1. Квадрат суммы Доказательство: К таблице К содержанию
Cлайд 5
2. Квадрат разности К таблице К содержанию Доказательство:
Cлайд 6
3. Разность квадратов К таблице К содержанию Доказательство:
Cлайд 7
4. Куб суммы К таблице К содержанию Доказательство:
Cлайд 8
5. Куб разности К таблице К содержанию Доказательство:
Cлайд 9
6. Сумма кубов К таблице К содержанию Доказательство:
Cлайд 10
7. Разность кубов К таблице К содержанию Доказательство:
Cлайд 11
Вынесение общего множителя за скобки Из каждого слагаемого, входящего в многочлен, выносится некоторый одночлен, входящий в качестве множителя во все слагаемые. Таким общим множителем может быть не только одночлен, но и многочлен.
Cлайд 12
Алгоритм нахождения общего множителя нескольких одночленов Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, - он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов). Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени. Произведение коэффициента, найденного на первом шаге, является общим множителем, который целесообразно вынести за скобки.
Cлайд 13
Пример Разложить на множители: x4y3 - 2x3y2 + 5x2. Воспользуемся сформулированным алгоритмом. Наибольший общий делитель коэффициентов –1, -2 и 5 равен 1. Переменная x входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки x2. Переменная y входит не во все члены многочлена; значит, ее нельзя вынести за скобки. Вывод: за скобки можно вынести x2. Правда, в данном случае целесообразнее вынести -x2. Получим: -x4y3-2x3y2+5x2=-x2(x2y3+2xy2-5). К содержанию
Cлайд 14
Способ группировки Бывает, что члены многочлена не имеют общего множителя, но после заключения нескольких членов в скобки (на основе переместительного и сочетательного законов сложения) удается выделить общий множитель, являющийся многочленом.
Cлайд 15
Алгоритм разложения многочлена на множители способом группировки: 1. Сгруппировать его члены так, чтобы слагаемые в каждой группе имели общий множитель 2. Вынести в каждой группе общий множитель в виде одночлена за скобки 3. Вынести в каждой группе общий множитель (в виде многочлена) за скобки.
Cлайд 16
Для уяснения сути способа группировки рассмотрим следующий пример: разложить на множители многочлен xy–6+3x–2y
Cлайд 17
Первый способ группировки: xy-6+3x-2y= =(xy-6)+(3x-2y). Группировка неудачна.
Cлайд 18
Второй способ группировки xy-6+3x-2y=(xy+3x)+(-6-2y)= =x(y+3)-2(y+3)= =(y+3)(x-2).
Cлайд 19
Третий способ группировки: xy-6+3y-2y=(xy-2y)+(-6+3x)= =y(x-2)+3(x-2)= =(x-2)(y+3).
Cлайд 20
Как видите, не всегда с первого раза группировка оказывается удачной. Если группировка оказалась неудачной, откажитесь от нее, ищите иной способ. По мере приобретения опыта вы будете быстро находить удачную группировку. xy-6+3y-2y=(x-2)(y+3). К содержанию
Cлайд 21
Разложение квадратного трехчлена на множители
Cлайд 22
К содержанию
Cлайд 23
Спасибо за внимание! Богданова А.В. г. Миасс
